Bellman-Ford的队列优化

Bellman-Ford算法在每实施依次松弛后，就会有一些顶点已经求得最短路，此后这些顶点的最短路的估计值就会一直不变，不再收后续松弛操作的影响，但是每次还要判断是否需要松弛，这就浪费时间了。

从上面可以得到启发：每次仅对最短路估计值发生变化了的顶点的所有出边执行松弛操作。

but，如何知道当前哪些点的最短路程发生了变化呢？

这里可以用一个队列来维护这些点，算法大致如下：

　　每次选取队首顶点u，对顶点u的所有出边进行松弛操作。例如有一条u->v的边，如果通过u->v这条边使得源点到顶点v的最短路程变短

(dis[u]+e[u][v]<dis[v]),且顶点v不在当前的队列中，就将顶点v放入队尾。

　　需要注意的是，同一个顶点同时在队列中出现多次是没有意义的，所以需要一个数组来判重(判断哪些点已经在队列中)。

　　在对顶点u的所有出边松弛完毕后，就将顶点u出队。

　　接下来不断从队列中取出新的队首顶点再进行如上操作，直到队列空为止。

对于上图，采用队列优化的方法求得最短路径。

下面是代码实现，用邻接矩阵来存储这个图，具体如下：

#include <stdio.h>

#define INF 999999
int book[];              //初始化为顶点都不在队列
int que[];              // 松弛成功并且顶点不在队列则并入队列

int main(int argc, char const *argv[])
{
    int i, j, n, m;
    int q1, q2, q3;
    int dis[], e[][];
    int head, tail;
    //读入n和m，n表示顶点个数，m表示边的个数
    scanf_s("%d %d", &n, &m);
    //初始化邻接矩阵
    for (i = ; i <= n; ++i)
    {
        for (j = ; j <= n; ++j)
        {
            if (i == j)
            {
                e[i][j] = ;
            }
            else
            {
                e[i][j] = INF;
            }
        }
    }
    //输入边
    for (i = ; i <= m; ++i)
    {
        scanf_s("%d %d %d", &q1, &q2, &q3);
        e[q1][q2] = q3;
    }

    //初始化dis数组
    for (i = ; i <= n; ++i)
    {
        dis[i] = INF;
    }
    dis[] = ;              //初始化dis[1]为0，其他为∞

    head = tail = ;
    que[tail] = ;           //1号顶点入队
    tail++;
    book[] = ; //标记1号顶点已经入队
    while (head < tail) //队列不为空的时候循环
    {
        for (i = ; i <= n; ++i)
        {
            if (e[que[head]][i] != INF && dis[i] > dis[que[head]] + e[que[head]][i])
            {
                dis[i] = dis[que[head]] + e[que[head]][i];
                if (!book[i])               //顶点不在队列，加入队列
                {
                    book[i] = ;
                    que[tail++] = i;
                }
            }
        }
        //出队
        book[que[head]] = ;    //重新标记不在队列
        head++;                 //相当于出队
    }

    printf("最终结果为：\n");
    for (i = ; i <= n; ++i)
    {
        printf(" 1号顶点到%d号顶点的最短距离为：%d\n", i, dis[i]);
    }
    printf("\n");
    getchar();
    getchar();
    return ;
}

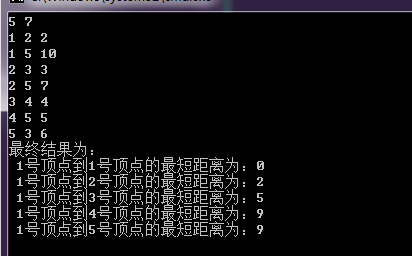
　　下面总结一下。初始时将源点加入队列。每次从队首（head）取出一个顶点，并对与其相邻的所有顶点进行松弛尝试，若某个相邻的顶点松弛成功，且这个相邻的顶点不在队列中（不在head和tail之间），则将它加入到队列中。对当前顶点处理完毕后立即出队，并对下一个新队首进行如上操作，直到队列为空算法结束。

　　使用队列优化的Bellman-Ford算法在形式上与广度优先搜索非常类似，不同的是在广度优先搜索的时候一个顶点出队后通常就不会再重新进入队列。而队列优化的Bellman-Ford算法一个顶点很可能在出队列之后再次被放入队列，也就是当一个顶点的最短路程估计值变小后，仍需要对其所有出边再次进行松弛，这样才能保证相邻顶点的最短路程估计值同步更新。

　　如何判断通过队列优化的Bellman-Ford算法一个图有负环呢？

　　如果某个点进入队列的次数超过n次，那么这个图肯定存在负环。

　　使用队列优化的Bellman-Ford算法的关键之处在于：只有那些在前一遍松弛中改变了最短路程估计值的点，才可能引起它们邻接点最短路程估计值发生改变。