【BZOJ1492】【NOI2007】货币兑换

我果然不会斜率优化

原题：

小Y最近在一家金券交易所工作。该金券交易所只发行交易两种金券：A纪念券（以下简称A券）和 B纪念券（以下

简称B券）。每个持有金券的顾客都有一个自己的帐户。金券的数目可以是一个实数。每天随着市场的起伏波动，

两种金券都有自己当时的价值，即每一单位金券当天可以兑换的人民币数目。我们记录第 K 天中 A券 和 B券 的

价值分别为 AK 和 BK（元/单位金券）。为了方便顾客，金券交易所提供了一种非常方便的交易方式：比例交易法

。比例交易法分为两个方面：（a）卖出金券：顾客提供一个 [0,100] 内的实数 OP 作为卖出比例，其意义为：将

 OP% 的 A券和 OP% 的 B券 以当时的价值兑换为人民币；（b）买入金券：顾客支付 IP 元人民币，交易所将会兑

换给用户总价值为 IP 的金券，并且，满足提供给顾客的A券和B券的比例在第 K 天恰好为 RateK；例如，假定接

下来 3 天内的 Ak、Bk、RateK 的变化分别为：

假定在第一天时，用户手中有 100元 人民币但是没有任何金券。用户可以执行以下的操作：

注意到，同一天内可以进行多次操作。小Y是一个很有经济头脑的员工，通过较长时间的运作和行情测算，他已经

知道了未来N天内的A券和B券的价值以及Rate。他还希望能够计算出来，如果开始时拥有S元钱，那么N天后最多能

够获得多少元钱。

2.必然存在一种最优的买卖方案满足：

每次买进操作使用完所有的人民币；

每次卖出操作卖出所有的金券。

n<=100000

 

神题QAQ

cdq太神了QAQ

恩首先需要想到一个思路非常鬼畜的基础dp： 令f[i]为第i天把钱花光最多能持有多少A券，则

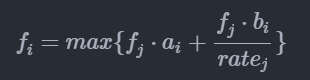
f[i]这么鬼畜的意义我是想不到啊QAQ

恩这道题从一开始就鬼畜了起来

根据得出的基础dp可以写出n^2的程序，显然优化对吧，斜率优化（为啥要斜率优化？我不懂啊QAQ

然后令j比k优，就酱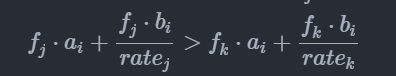

令g[i]=f[i]/rate[i]，酱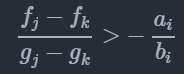

然后就斜率优化了，但是维护凸包似乎很麻烦（我不会QAQ），splay不好写，我们cdq分治

具体咋整，看代码意会吧我讲不清楚QAQ

方便以后常看所以代码加了注释QAQ

代码：（抄黄学长的QAQ

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 #include<cmath>
 using namespace std;
 const double inf=1e20;
 const double eps=2e-;
 struct nds{double x,y,a,b,k,rt;  int w,id;}a[],tmp[];
 int n;
 double f[];
 int stck[],tp=;
 double gtk(int x,int y){
     if(!y)  return -inf;
     if(fabs(a[x].x-a[y].x)<eps)  return inf;
     return (a[y].y-a[x].y)/(a[y].x-a[x].x);
 }
 void cdq(int l,int r){
     if(l==r){
         f[l]=max(f[l],f[l-]);
         a[l].y=f[l]/(a[l].a*a[l].rt+a[l].b);//y是a券的个数
         a[l].x=a[l].rt*a[l].y;//x是b券
         return ;
     }
     int md=(l+r)>>;  int t1=l,t2=md+;
     for(int i=l;i<=r;++i)  tmp[(a[i].id<=md?t1:t2)++]=a[i];
     for(int i=l;i<=r;++i)  a[i]=tmp[i];//先按照原来id左右划分
     cdq(l,md);//中序cdq
     tp=;
     for(int i=l;i<=md;++i){
         while(tp> && gtk(stck[tp-],stck[tp])<gtk(stck[tp-],i)+eps)  --tp;        stck[++tp]=i;
     }//搞左边的凸包
     stck[++tp]=;
     for(int i=md+,j=;i<=r;++i){
         while(j<tp && gtk(stck[j],stck[j+])+eps>a[i].k) ++j;
         f[a[i].id]=max(f[a[i].id],a[stck[j]].x*a[i].a+a[stck[j]].y*a[i].b);
     }//更新答案
     cdq(md+,r);
     t1=l,t2=md+;
     for(int i=l;i<=r;++i){
         if(t1>md)  tmp[i]=a[t2++];
         else if(t2>r)  tmp[i]=a[t1++];
         else  tmp[i]=a[(a[t1].x<a[t2].x||(fabs(a[t1].x-a[t2].x)<eps&&a[t1].y<a[t2].y)?t1:t2)++];
     }//按x第一y第二优先级排序，方便上一层搞凸包a
     for(int i=l;i<=r;++i)  a[i]=tmp[i];
 }
 bool cmp(nds a,nds b){  return a.k>b.k;}
 int main(){freopen("ddd.in","r",stdin);
     scanf("%d%lf",&n,&f[]);
     for(int i=;i<=n;++i){
         scanf("%lf%lf%lf",&a[i].a,&a[i].b,&a[i].rt);
         a[i].k=-a[i].a/a[i].b,a[i].id=i;
     }
     sort(a+,a+n+,cmp);//没想明白对k排序的意义QAQ
     cdq(,n);
     printf("%.3lf\n",f[n]);
     return ;
 }