KM算法详解[转]

KM算法详解

原帖链接：http://www.cnblogs.com/zpfbuaa/p/7218607.html#_label0

阅读目录

• 二分图博客推荐
• 匈牙利算法步骤
• 匈牙利算法博客推荐
• KM算法步骤
• KM算法标杆(又名顶标)的引入
• KM流程详解
• KM算法博客推荐

0.二分图

二分图的概念

二分图又称作二部图，是图论中的一种特殊模型。

设G=(V, E)是一个无向图。如果顶点集V可分割为两个互不相交的子集X和Y，并且图中每条边连接的两个顶点一个在X中，另一个在Y中，则称图G为二分图。

可以得到线上的driver与order之间的匹配关系既是一个二分图。

二分图的判定

无向图G为二分图的充分必要条件是，G至少有两个顶点，且其所有回路的长度均为偶数。

判断无向连通图是不是二分图，可以使用深度优先遍历算法（又名交叉染色法）。

下面着重介绍下交叉染色法的定义与原理

首先任意取出一个顶点进行染色,和该节点相邻的点有三种情况:

       1.如果节点没有染过色，就染上与它相反的颜色，推入队列，

       2.如果节点染过色且相反，忽视掉，

       3.如果节点染过色且与父节点相同，证明不是二分图，return

回到顶部

二分图博客推荐

代码可参考博客： 图论入门———深度优先搜索实现二分图判定

交叉染色法博客推荐：交叉染色法判断二分图

另外附上二分图的性质博客：二分图的一些性质

---

1.KM算法初步

KM算法全称是Kuhn-Munkras，是这两个人在1957年提出的，有趣的是，匈牙利算法是在1965年提出的。 

增广路径

增广路径定义：

若P是图G中一条连通两个未匹配顶点的路径，并且属于M的边和不属于M的边(即已匹配和待匹配的边)在P上交替出现，则称P为相对于M的一条增广路径

（举例来说，有A、B集合，增广路由A中一个点通向B中一个点，再由B中这个点通向A中一个点……交替进行）

增广路径有如下特性： 

1. 有奇数条边 

2. 起点在二分图的X边，终点在二分图的Y边 

3. 路径上的点一定是一个在X边，一个在Y边，交错出现。 

4. 整条路径上没有重复的点 

5. 起点和终点都是目前还没有配对的点，其他的点都已经出现在匹配子图中 

6. 路径上的所有第奇数条边都是目前还没有进入目前的匹配子图的边，而所有第偶数条边都已经进入目前的匹配子图。奇数边比偶数边多一条边 

7. 于是当我们把所有第奇数条边都加到匹配子图并把条偶数条边都删除，匹配数增加了1.

 

例如下图，蓝色的是当前的匹配子图，红色表示未匹配的路径，目前只有边x0y0，然后通过x1找到了增广路径：x1y0->y0x0->x0y2 

增广路径有两种寻径方法，一个是深搜，一个是宽搜。

例如从x2出发寻找增广路径

• 如果是深搜，x2找到y0匹配，但发现y0已经被x1匹配了，于是就深入到x1，去为x1找新的匹配节点，结果发现x1没有其他的匹配节点，于是匹配失败，x2接着找y1，发现y1可以匹配，于是就找到了新的增广路径。
• 如果是宽搜，x1找到y0节点的时候，由于不能马上得到一个合法的匹配，于是将它做为候选项放入队列中，并接着找y1，由于y1已经匹配，于是匹配成功返回了。

相对来说，深搜要容易理解些，其栈可以由递归过程来维护，而宽搜则需要自己维护一个队列，并对一路过来的路线自己做标记，实现起来比较麻烦。

匈牙利算法

匈牙利算法，用于求二分图的最大匹配。何为最大匹配？假设每条边有权值，那么一定会存在一个最大权值的匹配情况。

回到顶部

匈牙利算法步骤

算法根据一定的规则选择二分图的边加入匹配子图中，其基本模式为：

1.初始化匹配子图为空 

2.While 找得到增广路径 

3.Do 把增广路径添加到匹配子图中

回到顶部

匈牙利算法博客推荐

KM深度优先遍历算法，其中附带讲解图可参考博客：趣写算法系列之–匈牙利算法

最大匹配的讲解博客：匈牙利算法（二分图）

KM算法

KM算法，用于求二分图匹配的最佳匹配。何为最佳匹配？就是带权二分图的权值最大的完备匹配称为最佳匹配。 那么何为完备匹配？X部中的每一个顶点都与Y部中的一个顶点匹配，或者Y部中的每一个顶点也与X部中的一个顶点匹配，则该匹配为完备匹配。

回到顶部

KM算法步骤

其算法步骤如下：

1.用邻接矩阵（或其他方法也行啦）来储存图，注意：如果只是想求最大权值匹配而不要求是完全匹配的话，请把各个不相连的边的权值设置为0。

2.运用贪心算法初始化标杆。

3.运用匈牙利算法找到完备匹配。

4.如果找不到，则通过修改标杆，增加一些边。

5.重复3，4的步骤，直到完全匹配时可结束。

回到顶部

KM算法标杆(又名顶标)的引入

二分图最佳匹配还是二分图匹配，所以跟和匈牙利算法思路差不多。

二分图是特殊的网络流，最佳匹配相当于求最大（小）费用最大流，所以FF算法（全名Ford-Fulkerson算法）也能实现。

• 所以我们可以把这匈牙利算法和FF算法结合起来。这就是KM算法的思路了：尽量找最大的边进行连边，如果不能则换一条较大的。
• • FF算法里面，我们每次是找最长（短）路进行通流，所以二分图匹配里面我们也按照FF算法找最大边进行连边！
  • 但是遇到某个点被匹配了两次怎么办？那就用匈牙利算法进行更改匹配！
• 所以，根据KM算法的思路，我们一开始要对边权值最大的进行连线。
• 那问题就来了，我们如何让计算机知道该点对应的权值最大的边是哪一条？或许我们可以通过某种方式记录边的另一端点，但是呢，后面还要涉及改边，又要记录边权值总和，而这个记录端点方法似乎有点麻烦。
• • 于是KM采用了一种十分巧妙的办法（也是KM算法思想的精髓）：添加标杆(顶标)

添加标杆(顶标)流程：

• 我们对左边每个点Xi和右边每个点Yi添加标杆Cx和Cy。其中我们要满足Cx+Cy>=w[x][y]（w[x][y]即为点Xi、Yi之间的边权值）
• 对于一开始的初始化，我们对于每个点分别进行如下操作：Cx=max(w[x][y]);  Cy=0;

添加顶标之前的二分图：

                

添加顶标之后的二分图：

 

回到顶部

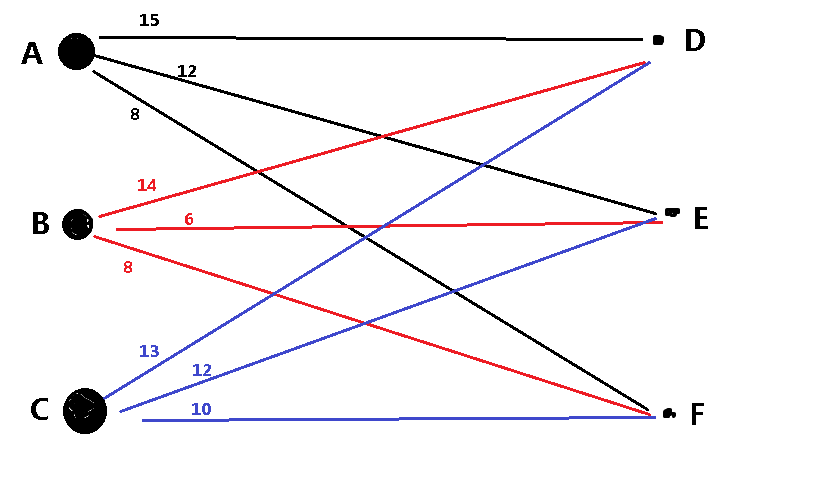
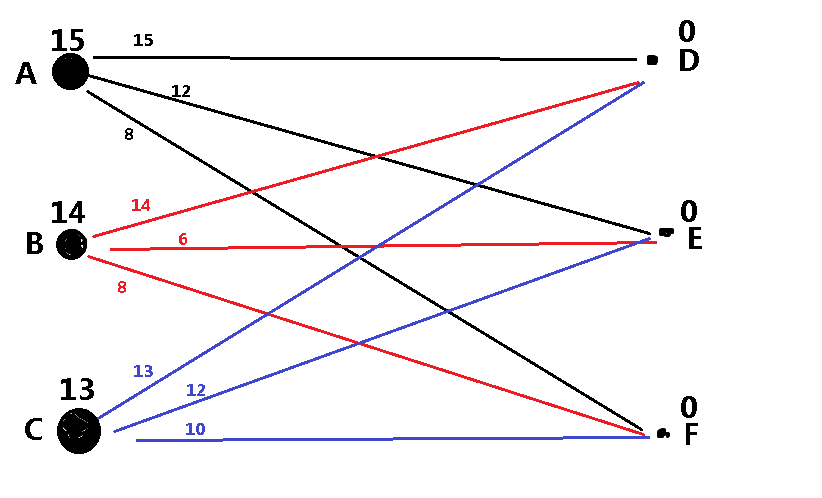
KM流程详解

• 初始化可行顶标的值 (设定lx,ly的初始值)
• 用匈牙利算法寻找相等子图的完备匹配
• 若未找到增广路则修改可行顶标的值
• 重复(2)(3)直到找到相等子图的完备匹配为止

使用上图的例子，采用匈牙利算法进行连边操作，将最大边进行连线。所以原来判断是否有边的条件w[x][y]==0换成了 Cx+Cy==w[x][y]

• 于是乎我们连了AD，形成一个新的二分图（我们下面叫它二分子图好了）
• 接下来就尴尬了，计算机接下来要连B点的BD，但是D点已经和A点连了，怎么办呢？？？
• • 根据匈牙利算法，我们做的是将A点与其他点进行连线，但此时的子图里“不存在”与A点相连的其他边，怎么办呢？？？
  • • 为此，我们就需要加上这些边！很明显，我们添边，自然要加上不在子图中边权最大的边，也就是和子图里这个边权值差最小的边。
    • • 于是，我们再一度引入了一变量d，d=min{Cx[i]+Cy[j]-w[i][j]}，其中，在这个题目里Cx[i]指的是A的标杆，Cy[j]是除D点（即已连点）以外的点的标杆。
      • • 随后，对于原先存在于子图的边AD，我们将A的标杆Cx[i]减去d，D的标杆Cy[d]加上d。
        • • 这样，这就保证了原先存在AD边保留在了子图中，并且把不在子图的最大权值的与A点相连的边AE添加到了子图。
          • 因为计算机判断一条边是否在该子图的条件是其两端的顶点的标杆满足Cx+Cy==w[x][y]
          • • 对于原先的边，我们对左端点的标杆减去了d，对右端点的标杆加上了d，所以最终的结果还是不变，仍然是w[x][y]。
            • 对于我们要添加的边，我们对于左端点减去了d，即Cx[i]=Cx[i]-d;为方便表示我们把更改后的的Cx[i]视为Cz[i]，即Cz[i]=Cx[i]-d;
            • • 因为Cz[i]=Cx[i]-d；d=Cx[i]+Cy[j]-w[i][j]；
              • 把d代入左式可得Cz[i]=Cx[i]-(Cx[i]+Cy[j]-w[i][j]);
              • 化简得Cz[i]+Cy[j]=w[i][j]；
              • 满足了要求！即添加了新的边。
  • 重复进行上述流程。（匈牙利算法以及FF算法的结合）

回到顶部

KM算法博客推荐

顶标内容讲的很好：KM算法

松弛度内容讲的比较好：二分图的最佳完美匹配——KM算法

匈牙利算法和FF算法结合得到KM算法讲的很详细：二分图匹配之最佳匹配——KM算法

最佳讲解博客推荐：我对KM算法的理解