图的最短路径——dijkstra算法和Floyd算法

dijkstra算法

　　求某一顶点到其它各个顶点的最短路径；已知某一顶点v0，求它顶点到其它顶点的最短路径，该算法按照最短路径递增的顺序产生一点到其余各顶点的所有最短路径。

对于图G={V,{E}};将图中的顶点分为两组:

　　第一组S：求出已知顶点的最短路径的集合

　　第二组V-S：尚未求出最短路径的顶点集合（开始为V-{v0}的全部顶点）

该算法将最短路径以递增顺序逐个将第二组顶点加入到第一组顶点中，直到所有的顶点都被加入到第一组顶点集S为止。

dijkstra算法和最小生树中的prim算法类似，都是把顶点看做集合，向所求集合中加点

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

const int INF=0x3f3f;
class Graph
{
    private:
        int num;
        int e;
        vector<vector<int> > arr;//存储图的邻接矩阵
        vector<bool> visit;//标记该结点是否用过
        vector<int> path;//从v0到其他结点的最短路径
    public:
        Graph();
        void dijkstra(const int &i);
};
Graph::Graph()
{
    cout<<" num"<<endl;
    cin>>num;
    cout<<" e"<<endl;
    cin>>e;

    visit.resize(num,false);
    path.resize(num);

    arr.resize(num);
    for(int i=;i<num;++i)
        arr.at(i).resize(num,INF);

    cout<<" 边的起始点和终点&&权值"<<endl;
    pair<int,int> p;
    for(int i=;i<e;++i)
    {
        cin>>p.first>>p.second;
        cin>>arr.at(p.first-).at(p.second-);
    }
}
void Graph::dijkstra(const int &index)
{
    //首先存储的是index结点到其他节点的最短路径的值
    for(int i=;i<num;++i)
        path.at(i)=arr.at(index-).at(i);
    //初始化visit
    visit.at(index-)=true;

    for(int check=;check<num-;++check)
    {
        int Min=INF,flag=;
        for(int i=;i<num;++i)
        {
            if(!visit.at(i)&&path.at(i)<Min)
            {
                flag=i;
                Min=path.at(i);
            }
        }
        visit.at(flag)=true;
        for(int i=;i<num;++i)//如果由于v0结点的加入导致index结点到其它接点的值变小更新path
        {
            if(path.at(i)>path.at(flag)+arr.at(flag).at(i))
                path.at(i)=path.at(flag)+arr.at(flag).at(i);
        }
    }
    for(int i=;i<num;++i)
        cout<<path.at(i)<<"\t";
    cout<<endl;
}
int main()
{
    Graph g;
    g.dijkstra();
    return ;
}

floyd算法

　　如果要让任意两点（例如从顶点a点到顶点b）之间的路程变短，只能引入第三个点（顶点k），并通过这个顶点k中转即a->k->b，才可能缩短原来从顶点a点到顶点b的路程。那么这个中转的顶点k是1~n中的哪个点呢？甚至有时候不只通过一个点，而是经过两个点或者更多点中转会更短。

　　当任意两点之间不允许经过第三个点时，这些城市之间最短路程就是初始路程

　　一：假如现在只允许经过1号顶点，求任意两点之间的最短路程，只需判断e[i][1]+e[1][j]是否比e[i][j]要小即可。e[i][j]表示的是从i号顶点到j号顶点之间的路程。e[i][1]+e[1][j]表示的是从i号顶点先到1号顶点，再从1号顶点到j号顶点的路程之和。其中i是1~n循环，j也是1~n循环

for (i = ; i <= n; i++)
        for (j = ; j <= n; j++)
        {
            if (e[i][j] > e[i][] + e[][j])
                e[i][j] = e[i][] + e[][j];
        }

　　在只允许经过1号顶点的情况下，任意两点之间的最短路程更新为

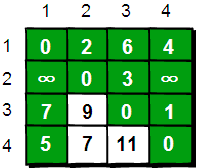
　　二：接下来继续求在只允许经过1和2号两个顶点的情况下任意两点之间的最短路程，我们需要在只允许经过1号顶点时任意两点的最短路程的结果下，再判断如果经过2号顶点是否可以使得i号顶点到j号顶点之间的路程变得更短。即判断e[i][2]+e[2][j]是否比e[i][j]要小，

//经过1号顶点
for(i=;i<=n;i++)
    for(j=;j<=n;j++)
        if (e[i][j]>e[i][]+e[][j])
            e[i][j]=e[i][]+e[][j];  

//经过2号顶点
for(i=;i<=n;i++)
    for(j=;j<=n;j++)
        if(e[i][j] > e[i][]+e[][j])
            e[i][j]=e[i][]+e[][j];

　　在只允许经过1和2号顶点的情况下，任意两点之间的最短路程更新为：

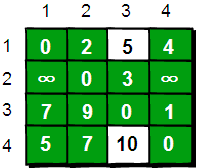
　　三：最后允许通过所有顶点作为中转

　　最开始只允许经过1号顶点进行中转，接下来只允许经过1和2号顶点进行中转……允许经过1~n号所有顶点进行中转，求任意两点之间的最短路程。用一句话概括就是：从i号顶点到j号顶点只经过前k号点的最短路程。

for(k=;k<=n;k++)//允许中转的k个结点
    for(i=;i<=n;i++)//源地点i
        for(j=;j<=n;j++)//目标地点j
            if(e[i][j]>e[i][k]+e[k][j])
                e[i][j]=e[i][k]+e[k][j];

code：求固定两地点的最短路径

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

const int INF=0x3f3f;
class Graph
{
    private:
        int num;
        int e;
        vector<vector<int> > arr;//存储图的邻接矩阵
        vector<int> path;//从v0到其他结点的最短路径
    public:
        Graph();
        void floyd(const int &begin,const int &end);
};
Graph::Graph()
{
    cout<<" num"<<endl;
    cin>>num;
    cout<<" e"<<endl;
    cin>>e;

    path.resize(num);

    arr.resize(num);
    for(int i=;i<num;++i)
        arr.at(i).resize(num,INF);

    cout<<" 边的起始点和终点&&权值"<<endl;
    pair<int,int> p;
    for(int i=;i<e;++i)
    {
        cin>>p.first>>p.second;
        cin>>arr.at(p.first-).at(p.second-);
    }
}
void Graph::floyd(const int &begin,const int &end)
{
    //允许经过的中转点;k==0,经过第一个中转点，==1经过第二个中转点(此时已经进过两个中转点
    //最多可以经过n个中转点)
    for(int k=;k<num;++k)
        if(arr.at(begin-).at(end-)>arr.at(begin-).at(k)+arr.at(k).at(end-))
            arr.at(begin-).at(end-)=arr.at(begin-).at(k)+arr.at(k).at(end-);

    cout<<arr.at(begin-).at(end-)<<endl;
}
int main()
{
    Graph g;
    g.floyd(,);
    return ;
}