Matrix 矩阵 那么什么是矩阵呢？

矩阵可以理解为方阵，只不过 平时方阵里面站着人 矩阵中是数值：

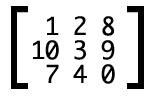
CSS3中的矩阵：

css3中的矩阵指的是一个方法，书写为matrix() 和 matrix3d(),前者是元素2D平面的移动变换(transfrom)，而后者是3D变换。2D变换矩阵3*3，如上图的示意图：3D变换则是4*4的矩阵。

可能有些难以理解 我们可以先看看其他东西 层层渐近-transform属性

.trans_skew { transform: skew(35deg); }

.trans_scale { transform:scale(1, 0.5); }

.trans_rotate { transform:rotate(45deg); }

.trans_translate { transform:translate(10px, 20px); }

扭曲（skew）缩放(scale) 旋转(rotate) 以及位移(translate)

那你有没有想过 为什么transform：rotate(45deg); 会让元素旋转45度 其后面作用的机理是什么呢。

下面这张图可以解释上面的疑问：

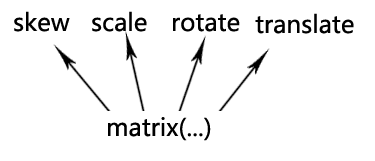
可以看到无论是旋转还是拉伸 本质上应用的都是matrix()方法实现的(修改matrix()方法固定的几个值)，只是类似于transform:rotate这种表现形式 我们更容易理解 记忆 与 上手。

换句话说理解transform中的matrix()矩阵方法有利于透彻理解CSS3中的transform属性。

矩阵应用场景和transform的坐标系统

实际上 在CSS3以及HTML5的世界里 矩阵matrix用的还是十分广泛的。 如 SVG和canvas

用过transform旋转的人可能发现了 其默认是绕着中心点旋转的，而这个中心点就是transform-origin属性对应的点。也就是矩阵计算的一个重要的依据点。

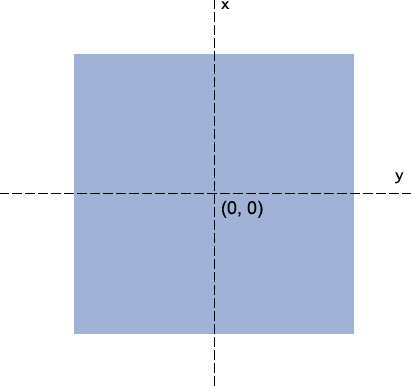
当我们通过transform-origin属性进行设置的时候，矩阵相关的计算也就随着而改变，反映到实际图像效果上就是 旋转拉伸的中心点变了！

举例来说：如果我们设置了元素的基点在左下角时：

-webkit-transform-origin: bottom left;

坐标中心就是左下角位置  于是动画(比如图片收缩)就是基于图片的左下角这一点了：

<head>

        <meta charset="UTF-8">

        <title></title>

        <style type="text/css">

            .anim_image {

                -webkit-transition: all 1s ease-in-out;

                -moz-transition: all 1s ease-in-out;

                transition: all 1s ease-in-out;

                cursor: pointer;

            }

            .anim_image_top {

                position: absolute;

                -webkit-transform: scale(0,0);

                opacity: 0;

            }

            .anim_box:hover .anim_image_top  {

                opacity: 1;

                -webkit-transform: scale(1,1);

                -webkit-transform-origin:top right;

            }

            .anim_box:hover .anim_image_bottom {

                    -webkit-transform: scale(0, 0);

                    -webkit-transform-origin: bottom left;

            }

        </style>

    </head>

    <body>

        <div id="testBox" class="demo anim_box">

            <img class="anim_image anim_image_top" src="../img/top.png" />

                <img class="anim_image anim_image_bottom" src="../img/bottom.png" />

        </div>

    </body>

</html>

可以运行一下 看看效果 分别是基于右上角 和 左上角的缩放。

可以在举个例子

transform-origin: 50px 70px;

中心点的位置移到了距离左侧50像素 顶部70像素的地方 而此时的(30,30)坐标则移到了图中白点的位置：

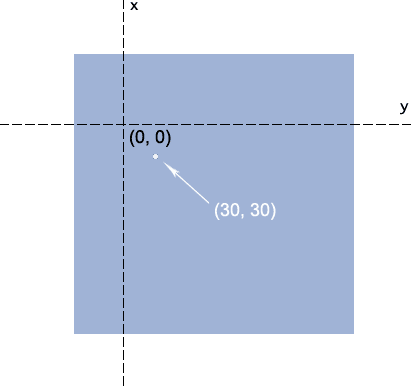
现在是不是很好理解了呢。

下面我们就跟着大神的脚步 来理解一下 2D matrix (哈哈 我也是看着大神的博客抄的。后面会贴出出处)

CSS3中 transform的matrix()方法 写法如下：

transform:matrix(a,b,c,d,e,f);

参数很复杂 达到了六个

实际上这六个参数对应的矩阵就是：

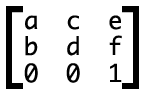
注意书写的方向是竖着的。

上面提过，矩阵可以想象成古代的士兵方阵，要让其发生变化，只有与另外一个士兵阵火拼就可以了，即使这是个小阵。

反应到这里 就是如下的转换公式

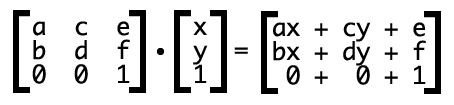
其中 x,y表示转换元素的所有坐标了 那后面的ax＋cy＋e是怎么来的呢？

很简单 3*3矩阵每一行的第一个值与后面1*3的第一个值相乘

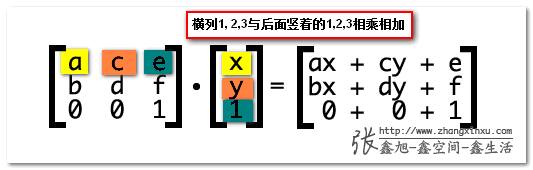
那ax+cy+e的意义是什么？

记住了，ax+cy+e为变换后的水平坐标，bx+dy+f表示变换后的垂直位置。

下面看一个例子：

transform: matrix(1, 0, 0, 1, 30, 30); /* a=1, b=0, c=0, d=1, e=30, f=30 */

现在 我们根据这个矩阵偏移元素的中心点，假设是(0,0)，即x=0 y = 0

于是，变换后的x坐标就是ax+cy+e = 1*0+0*0+30 =30, y坐标就是bx+dy+f = 0*0+1*0+30 =30.

于是，中心点坐标从(0, 0)变成了→(30, 30)。对照上面有个(30, 30)的白点图，好好想象下，原来(0,0)的位置，移到了白点的(30, 30)处，怎么样，是不是往右下方同时偏移了30像素哈！！

实际上transform: matrix(1, 0, 0, 1, 30, 30);就等同于transform: translate(30px, 30px);. 注意：translate, rotate等方法都是需要单位的，而matrix方法e, f参数的单位可以省略。

所以说 可以看出来 只要是中心点没有改变还是原来的(0,0) 那么matrix表现偏移就是

transform: matrix(与我无关, 哪位, 怎么不去高考, 打麻将去吧, 水平偏移距离, 垂直偏移距离);

你只要关心后面两个参数就可以了，至于前面4个参数，是牛是马，是男是女都没有关系的。

transform matrix矩阵与缩放，旋转以及拉伸

偏移是matrix效果中最简单，最容易理解的，因此，上面很详尽地对此进行展开说明。下面，为了进一步加深对matrix的理解，会简单讲下matrix矩阵与缩放，旋转以及拉伸效果。

缩放(scale)
上面的偏移只要关心最后两个参数，这个缩放也是只要关心两个参数。哪两个呢？

如果你足够明察秋毫，应该已经知道了，因为上面多次出现的：

transform: matrix(1, 0, 0, 1, 30, 30);

已经出卖了。

发现没，matrix(1, 0, 0, 1, 30, 30);的元素比例与原来一样，1:1, 而这几个参数中，有两个1, 啊哈哈！没错，这两个1就是缩放相关的参数。

其中，第一个缩放x轴，第二个缩放y轴。

用公式就很明白了，假设比例是s，则有matrix(s, 0, 0, s, 0, 0);，于是，套用公式，就有：
x' = ax+cy+e = s*x+0*y+0 = s*x;
y' = bx+dy+f = 0*x+s*y+0 = s*y;

也就是matrix(sx, 0, 0, sy, 0, 0);，等同于scale(sx, sy);

旋转(rotate)
旋转相比前面两个要更高级些，要用到（可能勾起学生时代阴影的）三角函数。

方法以及参数使用如下（假设角度为θ）：

matrix(cosθ,sinθ,-sinθ,cosθ,0,0)

结合矩阵公式，就有：

x' = x*cosθ-y*sinθ+0 = x*cosθ-y*sinθ

y' = x*sinθ+y*cosθ+0 = x*sinθ+y*cosθ

哎呀呀，四个参数，我记不住啊！莫慌，我们可以这样子记忆：
CS-SC：初三-上床，对称结构，这下忘不了了吧~~

不过，说句老实话，就旋转而言，rotate(θdeg)这种书写形式要比matrix简单多了，首先记忆简单，其次，无需计算。例如，旋转30°，前者直接：

transform:rotate(30deg);

而使用matrix表示则还要计算cos, sin值：

transform: matrix(0.866025,0.500000,-0.500000,0.866025,0,0);

拉伸(skew)
拉伸也用到了三角函数，不过是tanθ，而且，其至于b, c两个参数相关，书写如下（注意y轴倾斜角度在前）：

matrix(1,tan(θy),tan(θx),1,0,0)

套用矩阵公式计算结果为：

x' = x+y*tan(θx)+0 = x+y*tan(θx)

y' = x*tan(θy)+y+0 = x*tan(θy)+y

对应于skew(θx + "deg"，θy+ "deg")这种写法。

其中，θx表示x轴倾斜的角度，θy表示y轴，两者并无关联。

大神的博客在此 有兴趣的可以移步到此：http://www.zhangxinxu.com/wordpress/2012/06/css3-transform-matrix-矩阵/

HTML 学习笔记 CSS3 (2D Matrix)的更多相关文章

  1. HTML 学习笔记 CSS3 (2D转换)

    2.scaleX(<number>) : 使用 [sx,1] 缩放矢量执行缩放操作,sx为所需参数.scaleX表示元素只在X轴(水平方向)缩放元素,他的默认值是(1,1),其基点一样是在 ...

  2. A.Kaw矩阵代数初步学习笔记 4. Unary Matrix Operations

    “矩阵代数初步”(Introduction to MATRIX ALGEBRA)课程由Prof. A.K.Kaw(University of South Florida)设计并讲授. PDF格式学习笔 ...

  3. A.Kaw矩阵代数初步学习笔记 3. Binary Matrix Operations

    “矩阵代数初步”(Introduction to MATRIX ALGEBRA)课程由Prof. A.K.Kaw(University of South Florida)设计并讲授. PDF格式学习笔 ...

  4. css3学习笔记之2D转换

    translate() 方法 translate()方法,根据左(X轴)和顶部(Y轴)位置给定的参数,从当前元素位置移动. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 ...

  5. HTML 学习笔记 CSS3(Animation)

    CSS3动画: 通过CSS3 我们能够创建动画 这可以在许多网页中取代动画图片 Flash动画 以及JavaScript. CSS3 @keyframes 规则如需在 CSS3 中创建动画,您需要学习 ...

  6. HTML 学习笔记 CSS3(过度 transition)

    通过 CSS3,我们可以在不使用 Flash 动画或 JavaScript 的情况下,当元素从一种样式变换为另一种样式时为元素添加效果.请把鼠标移动到下面的元素上: 先看一下这个代码 实现旋转放大的效 ...

  7. ArcGIS API for JavaScript 4.2学习笔记[10] 2D添加指北针widget、视图保存、视图padding（第二章完结）

    这几个例子是第二章除了入门之外比较简单的几个,就做个合集,把最核心的代码(第二参数)和 引用放上来即可,不作多解释. 2D地图添加指北针widget 2D地图一般修正方向为正北方就需要这个widget ...

  8. 前端学习笔记--CSS3

    本本记录了css3的样式:浏览器支持度.圆角边框.阴影.文字与文本.过渡.动画.2d旋转.3d旋转 浏览器支持度: 1.圆角边框 例:只要确定了x.y值,就能知道弧度 画一个圆形:长=宽,border ...

  9. HTML 学习笔记 CSS3 (多列)

    CSS3多列 通过CSS3 我们能够创建多个列来对文本进行布局. 在这篇文章中 你将了解到如下多列属性: column-count column-gap column-rule 浏览器支持: 多列的属 ...

随机推荐

  1. IOS开发证书显示“此证书的签发者无效”解决方法

    今天早上同事说咱们的证书无法使用了,显示“此证书的签发者无效”.一开始以为谁误操作了证书,查看后发现所有证书都无效了.查了会才发下原来是Apple Worldwide Developer Relati ...

  2. 网络编程---HTTP

    URL: 什么是URL ? URL的全称是Uniform Resource Locator(统一资源定位符) 通过1个URL,能找到互联网上唯一的1个资源 URL就是资源的地址.位置,互联网上的每个资 ...

  3. xdebug + wincachegrind

    ;;;;;;;php.ini;;;;;;;;;;;;;;;;;; [Xdebug]zend_extension=D:\Xampp\php\ext\php_xdebug.dll;开启自动跟踪xdebug ...

  4. Team Leader炖完石头汤后干嘛

    在万众创业的互联网年代,挖人组建全明星团队过于奢侈.面对水平参差不齐的团队咋办? 命运真是捉弄,半年前在大美团打工时准备做个NABC的教学项目 ,结果自己就被挖到"Competitors 竞 ...

  5. 十大广泛使用的Linux发行版

    回到上世纪90年代,Mandrake Linux还是唯一的Linux发行版:而今天,Linux发行版的数量变得数不胜数.本文为大家整理出了十大广泛使用的Linux发行版,希望能帮助大家在选择合适的Li ...

  6. HTML <fieldset> 标签

    <div style="height:360px;width:180"> <fieldset> <legend> 用户管理 </legen ...

  7. Visual Studio 开发平台的安装与单元测试

    一.安装VS2013 1.运行安装文件夹中的.exe文件,选择好安装路径与所需功能后开始安装 2.安装后第一次打开,需要一段时间 3.安装成功后,要打开VS2013,在工具栏中找到帮助选项卡,点击注册 ...

  8. PHP代码规范

    PHP编码规范 1. 标识符命名规范 标识符的命名力求做到统一.达意和简洁. 1.1 统一 统一是指,对于同一个概念,在程序中用同一种表示方法,比如对于供应商,既可以用supplier,也可以用pro ...

  9. Apache虚拟主机配置

    在一个Apache服务器上可以配置多个虚拟主机,实现一个服务器提供多站点服务,其实就是访问同一个服务器上的不同目录.Apache虚拟主机配置有3中方法:基于IP配置.基于域名配置和基于端口配置,这里介 ...

  10. oracle数据泵示例

    主要的导出示例: 1.导出指定表空间: expdp system/xxx DIRECTORY=dump_dir tableapace=xxx dumpfile=xxx_%DATE:~0,4%%DATE ...