HDU 4513 吉哥系列故事——完美队形II （Manacher变形）

题意：假设有n个人按顺序的身高分别是h[1], h[2] ... h[n]，从中挑出一些人形成一个新的队形，新的队形若满足以下要求，则就是新的完美队形： 
　　1、连续的
　　2、形成回文串
　　3、从左到中间那个人，身高需保证不下降

　　　问有组成完美队形的最多人数

题解：Manacher算法的变形。

首先我们来解释一下Manacher算法：在我看来就是一个优化的暴力。

我们首先统一奇偶回文串成为奇数回文串，就是在两个数之间加入一些不可能出现的数。

例如题目：1 2 3 3 2 5 2 3 1—>（符号更加清楚）$ # 1 # 2 # 3 # 3 # 2 # 5 # 2 # 3 # 1 # &（其中首尾多的#保证答案正确） ，注意首尾多增加 & 与 $ 为了不处理边界。接着我们只需要统计此时回文串长度的一半（包括中间一个字符）再减一就是此处总回文串的长度。

首先使用dp数组记录回文串一半长度，id记录最大dp的下标，maxid记录最大dp可以管到的最后一个距离，然后利用回文串的性质减少每次比较的次数

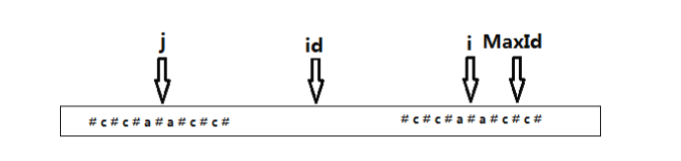
如图：在不超过maxid的位置（超过就不确定是否匹配成功了）j（i相对于id的对应位置）可以直接赋值给i，接着i再暴力寻找回文串是否没有找完整。最后我们的变形就在暴力处增加判断就好

#include<set>
#include<map>
#include<queue>
#include<stack>
#include<cmath>
#include<vector>
#include<string>
#include<cstdio>
#include<cstring>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;
#define eps 1E-8
/*注意可能会有输出-0.000*/
#define Sgn(x) (x<-eps? -1 :x<eps? 0:1)//x为两个浮点数差的比较,注意返回整型
#define Cvs(x) (x > 0.0 ? x+eps : x-eps)//浮点数转化
#define zero(x) (((x)>0?(x):-(x))<eps)//判断是否等于0
#define mul(a,b) (a<<b)
#define dir(a,b) (a>>b)
typedef long long ll;
typedef unsigned long long ull;
const int Inf=<<;
const double Pi=acos(-1.0);
const int Mod=1e9+;
const int Max=;
int num[Max];
int Init(int n)//增加其他字符，让奇数偶数回文串都变成奇数回文串
{
    for(int i=n-;i>=;--i)
    {
        num[(i<<)+]=num[i];
        num[(i<<)|]=;//不可能出现的字符
    }
    num[(n<<)|]=;
    num[]=;//边界
    num[(n<<)+]=;
    return (n<<)+;
}
int dp[Max];//每个位置匹配长度
int Manacher(int n)
{
    int manx=;
    int id=,maxid=;
    dp[]=;
    for(int i=;i<n;++i)
    {
        if(maxid>=i)
            dp[i]=min(dp[(id<<)-i],maxid-i+);
        else
            dp[i]=;
        while(num[i+dp[i]]==num[i-dp[i]]&&(num[i+dp[i]]==||num[i+dp[i]]<=num[i+dp[i]-]))//注意这儿需要修改
            dp[i]++;
        if(maxid<i+dp[i]-)
        {
            maxid=i+dp[i]-;
            id=i;
        }
        if(manx<dp[i]-)
            manx=dp[i]-;
    }
    return manx;
}
int main()
{
    int t,n;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        for(int i=;i<n;++i)
        scanf("%d",&num[i]);
        n=Init(n);
        printf("%d\n",Manacher(n));
    }
    return ;
}