【算法】BM算法

一. 字符串比较的分析

如果要判定长度为\(n\)两个字符串相等，比较中要进行\(n\)比较，但是如果要判定两个字符串不相等，只需要找出一个不相等的位置，因此可以得到如下结论：

结论1：判定字符串相等和判定字符串不相等的代价不同，判定不相等的代价更小

在KMP算法中，每发生一次失配时，算法总是尝试根据已经获得的匹配成功的信息来确定一个新的对齐位置，也即KMP算法是在尝试判断两个字符串相等，根据结论1，这种做法的代价要大于判定字符串不相等的代价。因此BM算法是尝试判定两个字符串不相等。

如果局部匹配成功，对于文本串\(P\)和局部的模式串\(partT\)，我们有如下结论：

结论2：

\[(P = partT)\Longrightarrow (\forall p\in P,\forall t\in partT \Longrightarrow p = t )
\]

因此文本串\(P\)和局部的模式串\(partT\)对应位置字符相等是匹配成功的一个必要条件，根据这个必要条件我们可以得到BM算法的朴素思想。

二.BM算法的思想

以下面插图为例：

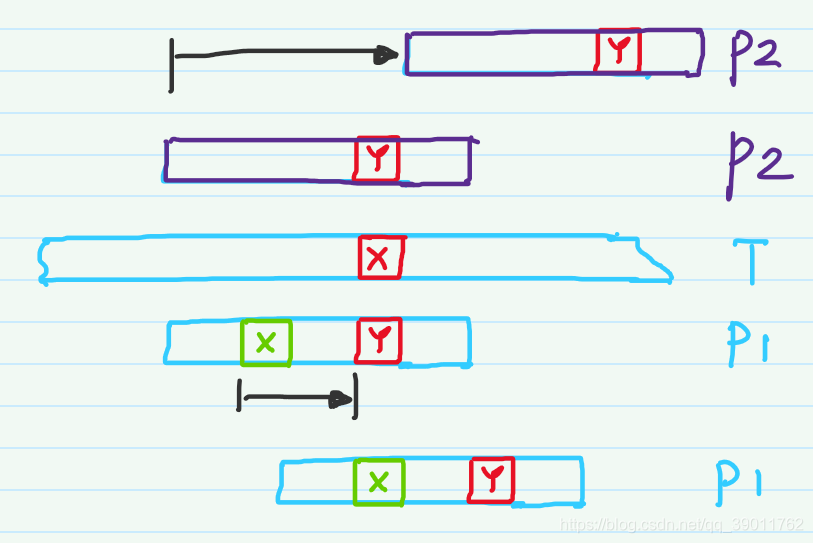
文本串\(T\)和模式串\(P_1\)进行匹配时，文本串中的字符X和模式串中的字符Y失配，此时需要重新选定匹配位置。观察模式串发现，在字符Y的前面，存在一个字符X，此时可以将绿色的X和红色的X对齐，然后再从头开始对比。

当模式串为\(P_2\)时，失配之后发现在字符Y的前面没有字符X，这说明了无论这部分进行怎样的局部匹配，最终都不可能匹配成功。因此可以直接跨过文本串字符X以前的位置。

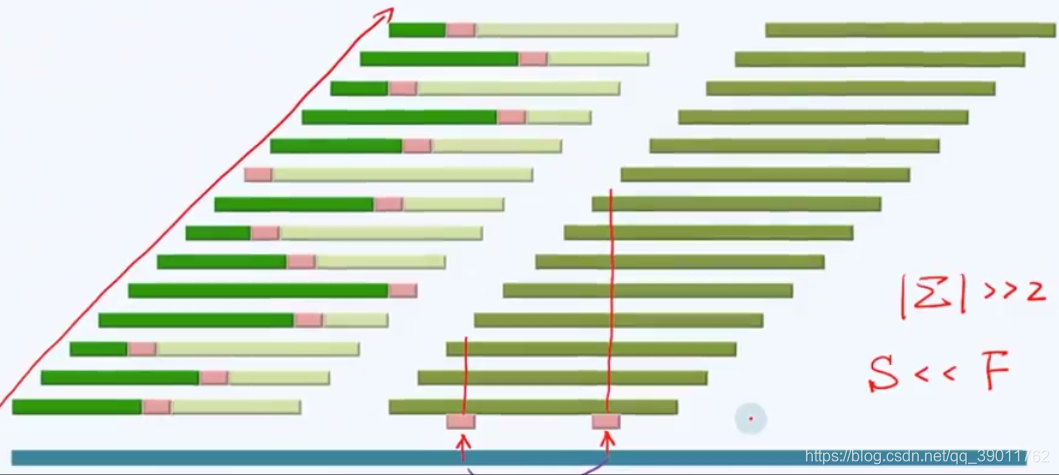
为了在一次失配出现时能够排除更多的对齐位置，我们考虑不同失配位置的信息量的大小。从下面的插图可以得到结论：

结论3：失配的位置越靠后，能够排除的对齐位置越多

因此BM算法不同于KMP算法，它的每次比对是逆向进行的。

图片来源

三.算法实现

只要我们记录下每个字符在模式串中的位置，当匹配失败时，找到一个新的位置进行比对即可，为此我们构造一个bc[ ]数组。

考虑两种边界情况：

• 模式串中的字符Y前面不存在字符X；
• 模式串中最右边的字符X在Y的后面；

第一种情况我们只需要令\(bc['X'] = -1\)即可，也就是使用通配哨兵。

第二种情况如果不特殊处理，会使模式串往回移动，出现该种情况使，我们只需要令模式串前进一个单位即可。

算法分为两个部分：构造bc[ ]数组和串匹配。

//构造bc[]
int *buildBc(const string &s){
    int *bc = new int [256];//一定要分配空间！！！
    for(int i = 0; i < 256; ++i)bc[i] = -1;
    for(int i = 0; i < s.size(); ++i)bc[s[i]] = i;
    return bc;
}
//串匹配
int bc(const string &s1, const string &s2){
    int *bc = buildBc(s2);
    int n = s1.size(), m = s2.size();
    int i = 0, j = 0;
    while(i + m < n){
        for(j = m - 1; j >= 0; --j){
            if(s1[i + j] != s2[j])break;
        }
        if(j < 0)break;
        int d = max(1, j - bc[s1[i + j]]);
        i += d;
    }
    return i;
}