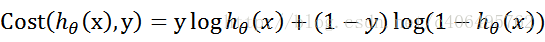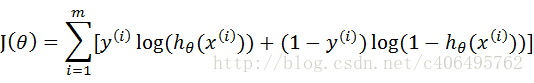logistics回归简单应用——梯度下降，梯度上升，牛顿算法（一）

警告：本文为小白入门学习笔记

由于之前写过详细的过程，所以接下来就简单描述，主要写实现中遇到的问题。

数据集是关于80人两门成绩来区分能否入学：

数据集：

http://openclassroom.stanford.edu/MainFolder/DocumentPage.php?course=DeepLearning&doc=exercises/ex4/ex4.html

假设函数（hypothesis function）：

--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

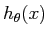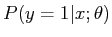2018.9.7补充

近日看了周志华的机器学习书，有对logistics回归（又叫对数几率回归，是一个分类算法）有了新的理解，所以将对其中的数学原理进行描述。

对于二分类问题，最理想的是用单位阶跃函数来表示，例如当x满足条件时，y=1或y=0，但是问题是它不是一个连续函数，所以需要用一个连续函数来替换，于是就用到了对数几率函数来替换

于是就得到上面那样的假设函数。它的返回结果其实是一个概率值，也就是某一个点它属于正样本或负样本的概率是多少，如果是正样本的概率大那就划分到正样本，负样本同理。

对于概率 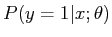 我们已经知道了训练样本中y和x的值，接下来如何求得参数theta的值。

首先补充一点概率论知识：

引自：https://blog.csdn.net/zengxiantao1994/article/details/72787849

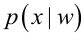
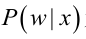
其中：p(w)：为先验概率，表示每种类别分布的概率：条件概率，表示在某种类别前提下，某事发生的概率。而为后验概率，表示某事发生了，并且它属于某一类别的概率，有了这个后验概率，我们就可以对样本进行分类。后验概率越大，说明某事物属于这个类别的可能性越大，我们越有理由把它归到这个类别下。

而我们需要求解的是后验问题，即知道某个样本是属于正类或负累，求解它是正类或负类的概率是多少。

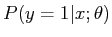对于这个我们该如何求参数theta和b呢？

于是，我们可以通过“”极大似然估计“”来估计theta和b的值。

总结起来，最大似然估计的目的就是：利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。

原理：极大似然估计是建立在极大似然原理的基础上的一个统计方法，是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。通过若干次试验，观察其结果，利用试验结果得到某个参数值能够使样本出现的概率为最大，则称为极大似然估计。

这里我就不推导公式，有兴趣可以查。求解参数的过程为：

　　（1）写出似然函数；

（2）对似然函数取对数，并整理；

（3）求导数；

（4）解似然方程。

最终的表达式是

求解这个可以用梯度下降方法或牛顿方法

--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

代价函数（cost function）：

使用梯度下降算法求解theta：

使用MATLAB实现：

function [jVal] = logCostFunction2(a)
%LOGCOSTFUNCTION2 此处显示有关此函数的摘要
% 此处显示详细说明
g = inline('1.0 ./ (1.0 + exp(-z))');
x = load('ex4x.dat');
y = load('ex4y.dat');
m = length(y);
x = [ones(m, ), x];
theta = zeros(size(x(,:)))'; %3*1
%theta = ones(,);
J = zeros(,);

for iter = :
w = zeros(,);
%梯度上升
for i = :m
c = x(i,:); %*
w = w + (g(c * theta) - y(i)) * c';
%w = w + (y(i) - g(c * theta)) * c';
end
%代价函数
f = ;
for j = :m
b = x(j,:);
f = f + (y(j) .* log(g(b * theta)) + ( - y(j)) .* log( - g(b * theta)));
end
%更新theta
theta = theta - (a * w / m);
%theta = theta + (a * w);
jVal = - ./ m .* f;
J(iter) = jVal;
end
disp(theta);
%迭代次数和代价函数值图像
figure();
plot(:,J(:),'r-');hold on;
xlabel('Number of iterations');
ylabel('Cost J');
%决策边界
figure();
x1 = x(:,);
x2 = - (theta() + theta() .* x1)./theta();
pos = find(y == );
neg = find(y == );
plot(x(pos,),x(pos,),'+');hold on;
plot(x(neg,),x(neg,),'o');hold on;
plot(x1(:m),x2,'r');
end

设置不同的learning rate，获得以下曲线：

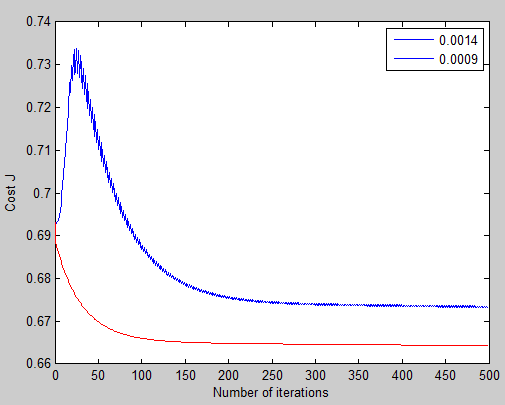
可以看出当alpha = 0.0014时，曲线是蓝色那条，可以看出曲线发生抖动，说明取值过大，其实我一开始就是应为选取alpha过大，导致一直获取抖动的曲线，还有就是迭代次数不够也会获取不到最小值。

决策边界：

theta0 = -0.0193
theta1 = 0.0474
theta2 = -0.0236

y = theta‘ * x；

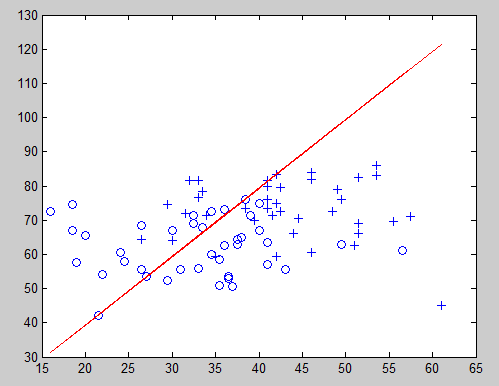
因为我是对照着开头网页上的内容去做的，那个网站上是使用牛顿算法求解，我使用的是梯度下降算法，我发现它们有很大误差，但是看迭代次数和损失函数图像，的确正常下降到最小值，但是误差怎么会这么大？百度了几篇博客学习：

----------------------------------------------------------------------------------------------------------------------------------------------

分界面怎么画呢？问题也就是在x1，x2坐标图中找到那些将x1，x2带入1/(1+exp(-wx))后，使其值>0.5的（x1,x2）坐标形成的区域，因为我们知道1/(1+exp(-wx))>0.5意味着该区域的（x1，x2）表示的成绩允许上大学的概率>0.5,那么其他的区域就是不被允许上大学，那么1/(1+exp(-wx))=0.5解出来的一个关于x1，x2的方程就是那个分界面。我们解出来以后发现，这个方程是一个直线方程：w（2）x1+w（3）x2+w（1）=0  注意我们不能因为这个分界面是直线，就认为logistic回归是一个线性分类器，注意logistic回归不是一个分类器，他没有分类的功能，这个logistic回归是用来预测概率的，这里具有分类功能是因为我们硬性规定了一个分类标准：把>0.5的归为一类，<0.5的归于另一类。这是一个很强的假设，因为本来我们可能预测了一个样本所属某个类别的概率是0.6，这是一个不怎么高的概率，但是我们还是把它预测为这个类别，只因为它>0.5.所以最后可能logistic回归加上这个假设以后形成的分类器
的分界面对样本分类效果不是很好，这不能怪logistic回归，因为logistic回归本质不是用来分类的，而是求的概率。

摘自 ： https://www.cnblogs.com/happylion/p/4169945.html

----------------------------------------------------------------------------------------------------------------------------------------------

对此我还有一个问题，我发现同一个问题有的人用梯度上升方法求解，而用梯度下降法也能求解，所以有对梯度上升和梯度下降进行了了解：

这是合并后的代价函数：

这个代价函数，是对于一个样本而言的。给定一个样本，我们就可以通过这个代价函数求出，样本所属类别的概率，而这个概率越大越好，所以也就是求解这个代价函数的最大值。既然概率出来了，那么最大似然估计也该出场了。

对比上面我使用的代价函数：

会发现区别，他们之间相差一个负号，这样就明白了。

于是我又用梯度上升方法实现一次：

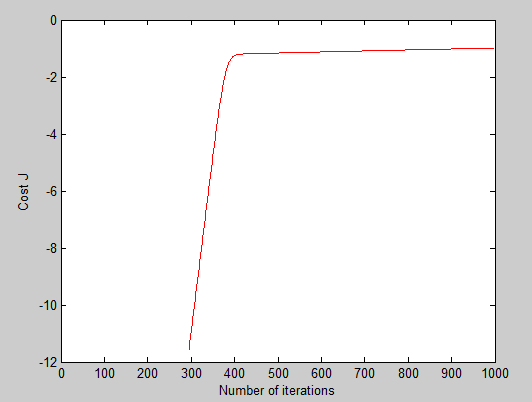
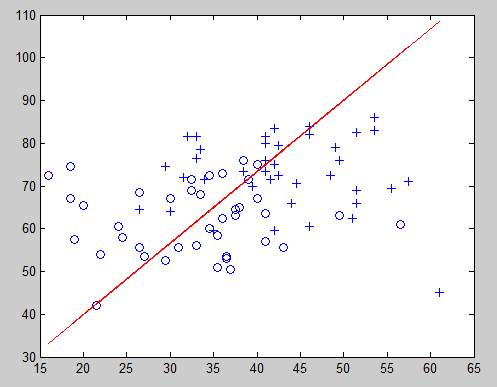
theta：

0.9781
0.2580
-0.1540

虽然alpha的取值，和最后theta值有很大的区别，但是最后的图像差不多一样不精确.

假如一个同学科目1为20 分，科目2为80分

0.21% 这个准确性的确很低

---------------------------------------------------------------------------------------------------------------------------------------------

对此我还是决定用牛顿方法再求解一次：

代价函数（cost Function）：

牛顿方法是：

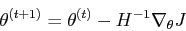
MATLAB实现：

function [ jVal ] = logNewton(  )
g = inline('1.0 ./ (1.0 + exp(-z))');
x = load('ex4x.dat');
y = load('ex4y.dat');
m = length(y);
x = [ones(m, ), x];
theta = zeros(size(x(,:)))'; %3*1
%theta = ones(,);
J = zeros(,);
for iter = :
    w = zeros(,);
    %求偏导
    for i = :m
        c = x(i,:); %*
        w = w + (g(c * theta) - y(i)) * c';
    end
    %Hessian
    f = ;
    for j = :m
        b = x(j,:);
        f = f + (g(b * theta) .* ( - g(b * theta)) * b' * b);
    end
     %代价函数
    l = ;
    for j = :m
        b = x(j,:);
        l = l + (y(j) .* log(g(b * theta)) + ( - y(j)) .* log( - g(b * theta)));
    end
    %更新theta
    theta = theta - ( f\ w); %inv（f）*w
    jVal = - ./ m .* l;
    J(iter) = jVal;
end
disp(theta);
%迭代次数和代价函数值图像
figure();
plot(:,J(:),'o--');hold on;
xlabel('Number of iterations');
ylabel('Cost J');
%决策边界
figure();
x1  = x(:,);
x2 =  - (theta() + theta() .* x1)./theta();
pos = find(y == );
neg = find(y == );
plot(x(pos,),x(pos,),'+');hold on;
plot(x(neg,),x(neg,),'o');hold on;
plot(x1(:m),x2,'r');
end

别人家的代码（只有迭代部分）：https://www.cnblogs.com/tornadomeet/archive/2013/03/16/2963919.html

for i = :MAX_ITR
    % Calculate the hypothesis function
    z = x * theta;
    h = g(z);%转换成logistic函数

    % Calculate gradient and hessian.
    % The formulas below are equivalent to the summation formulas
    % given in the lecture videos.
    grad = (/m).*x' * (h-y);%梯度的矢量表示法
    H = (/m).*x' * diag(h) * diag(1-h) * x;%hessian矩阵的矢量表示法

    % Calculate J (for testing convergence)
    J(i) =(/m)*sum(-y.*log(h) - (-y).*log(-h));%损失函数的矢量表示法

    theta = theta - H\grad;%是这样子的吗？
end

所以说熟练使用矩阵知识可以简单化很多问题。

图像：

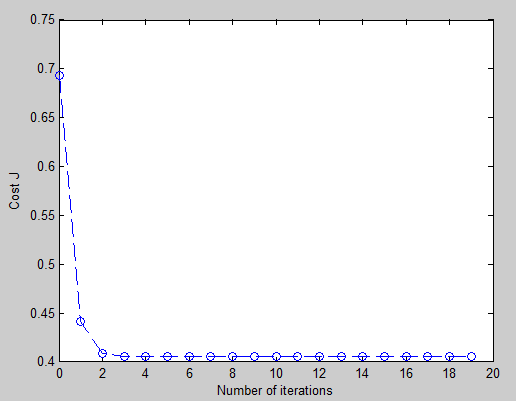
可以看出递归将近6次后就获取最小值；

决策边界：

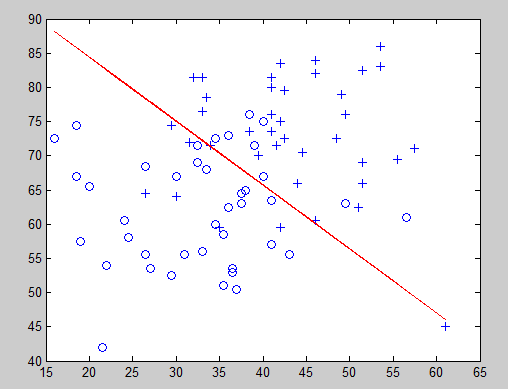
theta：

-16.3787
0.1483
0.1589

这样看起来要准确许多，接下来我们来预测一下，假如一个同学科目1为20 分，科目2为80分

那么被录取的可能性为33.17%