谱聚类算法(Spectral Clustering)优化与扩展

谱聚类(Spectral Clustering, SC)在前面的博文中已经详述，是一种基于图论的聚类方法，简单形象且理论基础充分，在社交网络中广泛应用。本文将讲述进一步扩展其应用场景:首先是User-Item协同聚类，即spectral coclustering，之后再详述谱聚类的进一步优化。

1 Spectral Coclustering

1.1 协同聚类(Coclustering)

在数据分析中，聚类是最常见的一种方法，对于一般的聚类算法(kmeans, spectral clustering, gmm等等)，聚类结果都类似图1所示，能挖掘出数据之间的类簇规律。

图1 聚类结果图

即使对于常见的数据User-Item评分矩阵(常见于各社交平台的数据之中，例如音乐网站的用户-歌曲评分矩阵，新闻网站的用户-新闻评分矩阵，电影网站的用户-电影评分矩阵等等)，如表1所示。在聚类分析中，也常常将数据计算成User-User的相似度关系或Item-Item的相似度关系，计算方法诸如应用Jaccard距离，将User或Item分别当成Item或User的特征，再在此基础上计算欧氏距离、cos距离等等。

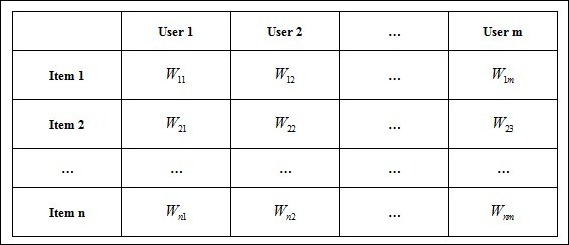
表1 User-Item评分矩阵

但是如果能聚类成如图2中的coclustering关系，将User和Item同时聚类，将使得数据结果更具意义，即在音乐网站中的用户和歌曲coclustering结果表明，某些用户大都喜欢某类歌曲，同时这类歌曲也大都只被这群用户喜欢着。这样，不管是用于何种场景(例如歌曲推荐)，都将带来极大的益处。

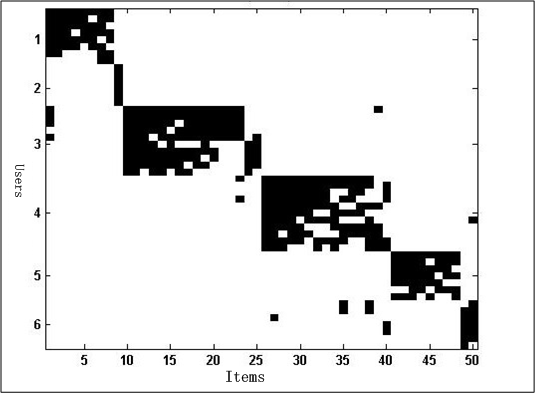图2 coclustering图

1.2 Spectral Coclustering

对于User-Item评分矩阵，这是一个典型的二部图(Bipartite Grap)，Item-User矩阵A，假设A为N*M，即N个item和M个user，可展开成:

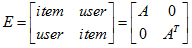其中E为(M+N)*(M+N)的方阵，且对称。

对于A的二部图，只存在Item与User之间的邻接边，在Item(User)之间不存在邻接边。再用谱聚类原理——将带权无向图划分为两个或两个以上的最优子图，使子图内部尽量相似，而子图间距离尽量距离较远。这样的聚类结果将Cut尽量少的边，分割出User和Item的类，如果类记C_i(U,I)为第i个由特定的User和Item组成的类，由谱聚类原理，Cut掉的C_i边为中的User或Item与其它类C_j(j≠i)的边，且其满足某种最优Cut方法，简单地说，Cut掉的User到其它类C_j(j≠i)的Item的边，可理解为这些User与其它Item相似关系较小；同样Cut掉的Item到其它类C_j(j≠i)的User的边，可理解为这些Item与其它User相似关系较小。这正好满足coclusering的定义。

在谱聚类的基础上，再实现Spectral Coclustering，十分简单，将E直接当成谱聚类的邻接矩阵即可，至于求Laplacian矩阵、求特征值、计算Kmeans，完成与谱聚类相同。

PS:更多详情，请参见参考文献1。

2 谱聚类的半监督学习

假设有大量新闻需要聚类，但对于其中的部分新闻，编辑已经人工分类好了，例如(N_i1,N_i₂, …, N_im)，为分类好的第i类，那么对于人工分类好的数据，就相当于聚类中的先验知识(或正则)。

在聚类时，可相应在邻接矩阵E中增加类彼此间邻接边，并使得其邻接权重较大，这样生成的邻接矩阵为E’。这样，再对此邻接矩阵E’做谱聚类，聚类结果将在一定程度上维持人工分类的结果，并达到聚类的目的。

PS：更多详情，请参见参考文献2，不过谱聚类的半监督学习，都有点扯。

参考文献：

1 Inderjit S. Dhillon. Co-clustering documents and words using Bipartite Spectral Graph Partitioning;

2 W Chen. Spectral clustering: A semi-supervised approach;

3 Wen-Yen Chen, Yangqiu Song, Hongjie Bai, Chih-Jen Lin, Edward Y. Chang. Parallel Spectral Clustering in Distributed Systems.

----