leetcode 5/300 最长回文子串 py

目录

• 题目说明
• 方法一：动态规划——状态转移方程
• 方法二：优化中心扩展算法

题目说明

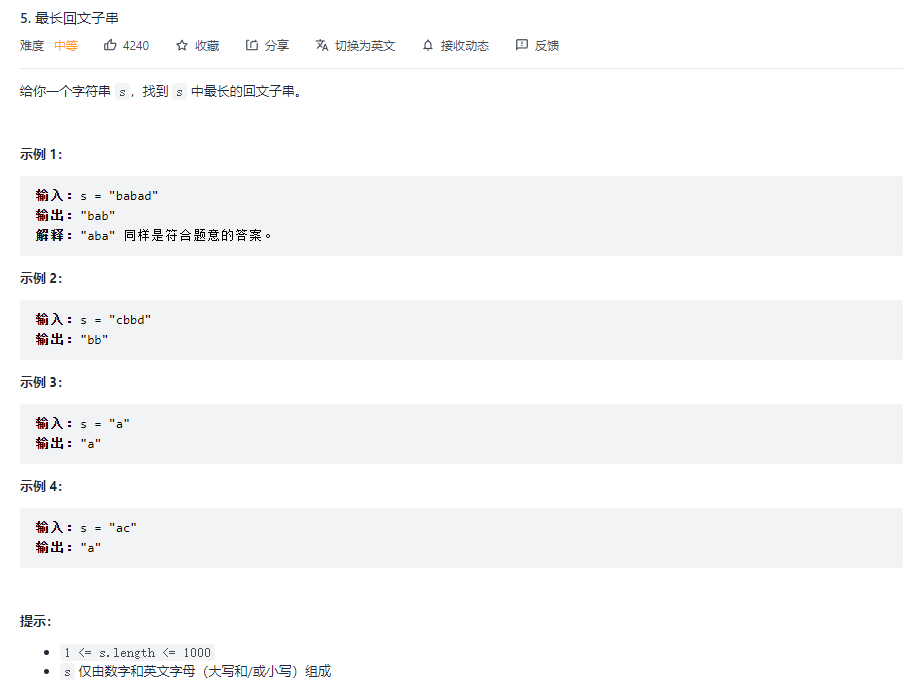
要看明白求得是什么，最长回文字串是指例如cababa中ababa是最长的，不是求回文的部分aba

方法一：动态规划——状态转移方程

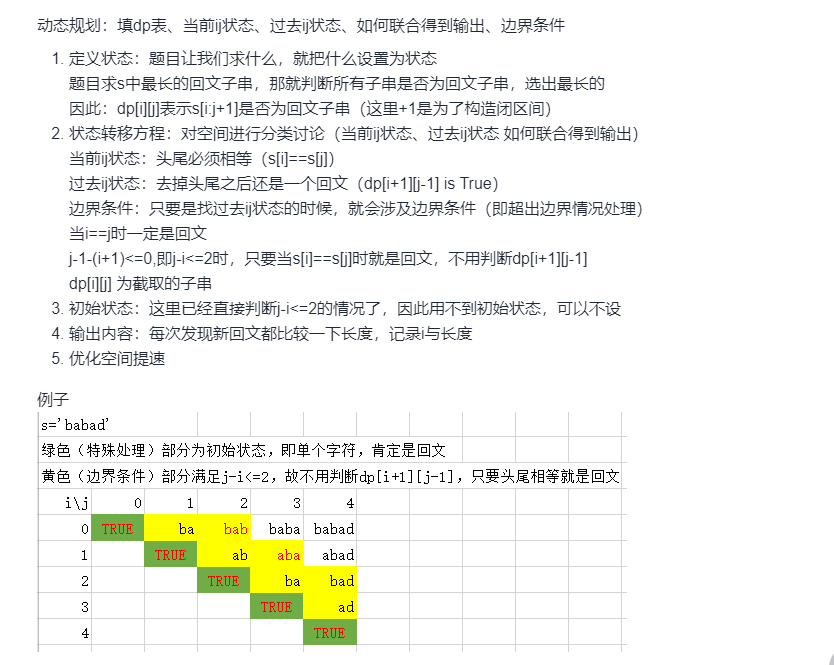
动态规划的要素

1. 如果可以把局部子问题的解结合起来得到全局最优解，那这个问题就具备最优子结构 ；

2. 如果计算最优解时需要处理很多相同的问题，那么这个问题就具备重复子问题。
   
   

class Solution:
    def longestPalindrome(self, s: str) -> str:

        size = len(s)
        # 特殊处理
        if size == 1:
            return s
        # 创建动态规划dynamic programing表
        dp = [[False for _ in range(size)] for _ in range(size)]
        #创建了一个5x5的，初始化为false的矩阵，false代表不是字串部分
        # 初始长度为1，这样万一不存在回文，就返回第一个值（初始条件设置的时候一定要考虑输出）
        max_len = 1
        start = 0
        for j in range(1,size):
            for i in range(j):
                # 边界条件：
                # 只要头尾相等（s[i]==s[j]）就能返回True
          '''''
          第一个if else是为了判断回文字串中是否有其他相等的部分，当小于2如aba，明显不存在，所以可以直接设为true
          当大于2，如ababa当判断第一个a和最后一个a时，需要在判断两个b是否相同。
          '''''
                if j-i<=2:
                    if s[i]==s[j]:
                        dp[i][j] = True
                        cur_len = j-i+1
                # 状态转移方程
                # 当前dp[i][j]状态：头尾相等（s[i]==s[j]）
                # 过去dp[i][j]状态：去掉头尾之后还是一个回文（dp[i+1][j-1] is True）
                else:
                    if s[i]==s[j] and dp[i+1][j-1]:
                        dp[i][j] = True
                        cur_len = j-i+1
                # 出现回文更新输出
                if dp[i][j]:
                    if cur_len > max_len:
                     #这里判断是否为最长的回文字串如abab有两个结果时，只会选择输出第一个最长的aba
                        max_len = cur_len
                        start = i

        return s[start:start+max_len]
'''
作者：_Breiman
链接：https://leetcode-cn.com/problems/longest-palindromic-substring/solution/5-zui-chang-hui-wen-zi-chuan-dong-tai-gu-p7uk/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
'''

方法二：优化中心扩展算法

思路：首先，我们进行拆解，从简单到复杂

1. 考虑中心到两边的数都等于中心，这样只需要考虑一边的情况，最后左右两边相减，得到最长
2. 考虑两边不等于中心，需要考虑左边是否等于右边
3. 对每次循环得到的最长子串进行判断，如果比上一次的长，则替换
   
   简而言之，就是找到一个i，从i依次向左向右判断是否相同。

#优化中心扩展算法以及由简单到全面的思路
class Solution:
    def longestPalindrome(self, s: str) -> str:
        # 长度为0 或者1时，直接返回原序列
        if len(s) < 2:
            return s
        maxstr = ''
        # 定义两个指针，一左一右
        left = 0
        right = 0
        for i in range(len(s)):
            left = i - 1
            right = i + 1
            while left > -1 and s[left] == s[i]:
                left -= 1
            while right < len(s) and s[right] == s[i]:
                right+=1
            while left>-1 and right<len(s) and s[left] == s[right]:
                left -= 1
                right += 1
            #这里边界需要注意，跳出循环的时候指针都超过范围了需要缩小，但是切片右边界不包括，因此需要加一，所以抵消
            maxstr = s[left+1:right] if right-left-1>len(maxstr) else maxstr
            '''
            可以看出，如果没有最长字串，那么最后会返回第一个字符。并且由于前面第三个while减一了，所以这里要加一，并且由于左闭右开，所以right不用变
            '''
        return maxstr
'''
作者：6GU30N7ObH
链接：https://leetcode-cn.com/problems/longest-palindromic-substring/solution/you-hua-zhong-xin-kuo-zhan-suan-fa-yi-ji-p30u/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
'''