开源项目｜Go 开发的一款分布式唯一 ID 生成系统

原文连接： 开源项目｜Go 开发的一款分布式唯一 ID 生成系统

今天跟大家介绍一个开源项目：id-maker，主要功能是用来在分布式环境下生成唯一 ID。上周停更了一周，也是用来开发和测试这个项目的相关代码。

美团有一个开源项目叫 Leaf，使用 Java 开发。本项目就是在此思路的基础上，使用 Go 开发实现的。

项目整体代码量并不多，不管是想要在实际生产环境中使用，还是想找个项目练手，我觉得都是一个不错的选择。

项目背景

在大部分系统中，全局唯一 ID 都是一个强需求。比如快递，外卖，电影等，都需要生成唯一 ID 来保证单号唯一。

那业务系统对 ID 号的要求有哪些呢？

全局唯一性：不能出现重复的 ID 号，既然是唯一标识，这是最基本的要求。
趋势递增：在 MySQL InnoDB 引擎中使用的是聚集索引，由于多数 RDBMS 使用 B-tree 的数据结构来存储索引数据，在主键的选择上面我们应该尽量使用有序的主键保证写入性能。
单调递增：保证下一个 ID 一定大于上一个 ID，例如事务版本号、IM 增量消息、排序等特殊需求。
信息安全：如果 ID 是连续的，恶意用户的扒取工作就非常容易做了，直接按照顺序下载指定 URL 即可；如果是订单号就更危险了，竞对可以直接知道我们一天的单量。所以在一些应用场景下，会需要 ID 无规则、不规则。

在此背景下，有一个高可用的唯一 ID 生成系统就很重要了。

项目使用

生成 ID 分两种方式：

根据数据库生成 ID。
根据雪花算法生成 ID。

使用上提供两种方式来调用接口：

HTTP 方式
gRPC 方式

HTTP 方式

1、健康检查：

curl http://127.0.0.1:8080/ping

2、获取 ID：

获取 tag 是 test 的 ID：

curl http://127.0.0.1:8080/v1/id/test

3、获取雪花 ID：

curl http://127.0.0.1:8080/v1/snowid

gRPC 方式

1、获取 ID：

grpcurl -plaintext -d '{"tag":"test"}' -import-path $HOME/src/id-maker/internal/controller/rpc/proto -proto segment.proto localhost:50051 proto.Gid/GetId

2、获取雪花 ID：

grpcurl -plaintext -import-path $HOME/src/id-maker/internal/controller/rpc/proto -proto segment.proto localhost:50051 proto.Gid/GetSnowId

本地开发

# Run MySQL

$ make compose-up

# Run app with migrations

$ make run

项目架构

项目使用 go-clean-template 架构模板开发，目录结构如下：

下面对各目录做一个简要说明：

cmd：程序入口
config：配置文件
docs：生成的项目文档
integration-test：整合测试
internal：业务代码
pkg：一些调用的包

借用官方的两张图：

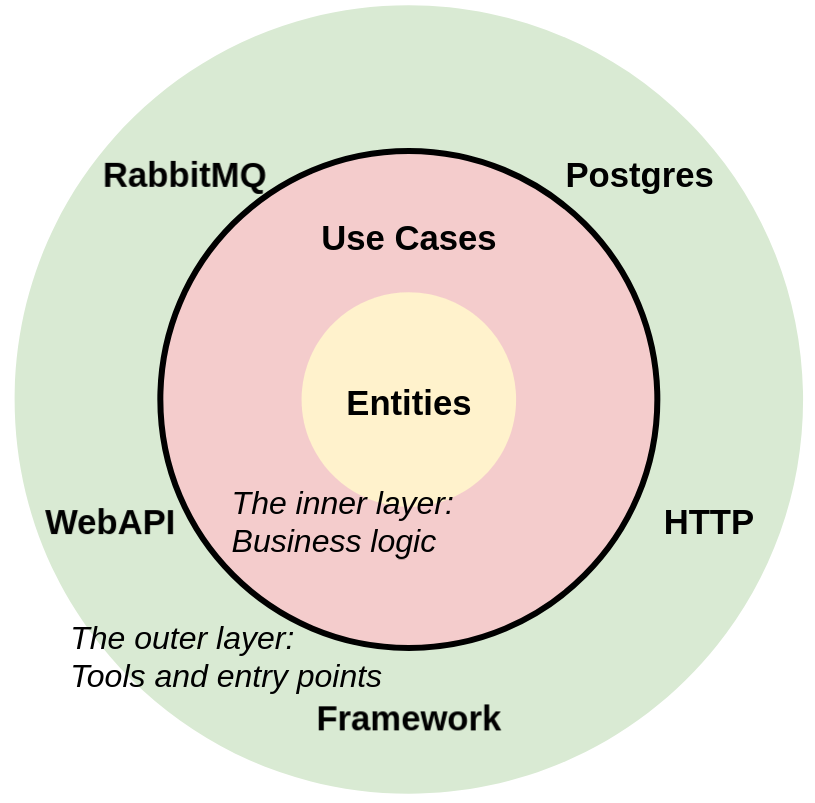
整体的层次关系是这样的，最里面是 models，定义我们的表结构，然后中间是业务逻辑层，业务逻辑层会提供接口，给最外层的 API 来调用，最外层就是一些工具和调用入口。

这样做的最大好处就是解耦，不管最外层如何变化，只要在业务逻辑层实现对应接口即可，核心代码可能根本不需要改变。

所以，它们之间的调用关系看起来是这样的：

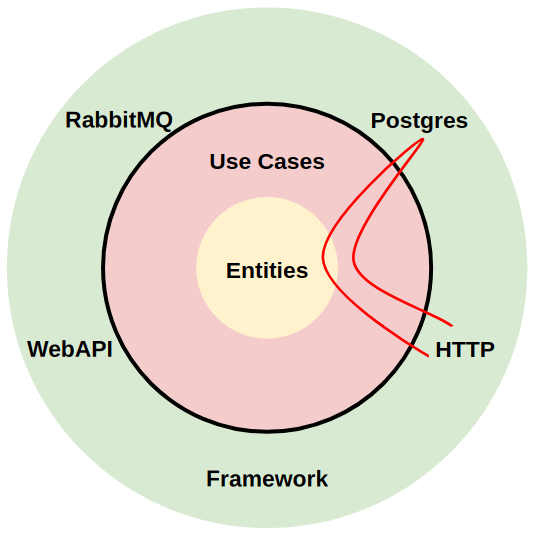
HTTP > usecase

       usecase > repository (Postgres)

       usecase < repository (Postgres)

HTTP < usecase

以上就是本项目的全部内容，如果大家感兴趣的话，欢迎给我留言交流，要是能给个 star 那就太好了。

项目地址： ：id-maker

往期文章：

推荐阅读：