ZFNet: Visualizing and Understanding Convolutional Networks

目录

• 论文结构
• 反卷积

ZFnet的创新点主要是在信号的“恢复”上面，什么样的输入会导致类似的输出，通过这个我们可以了解神经元对输入的敏感程度，比如这个神经元对图片的某一个位置很敏感，就像人的鼻子对气味敏感，于是我们也可以借此来探究这个网络各层次的功能，也能帮助我们改进网络。

论文结构

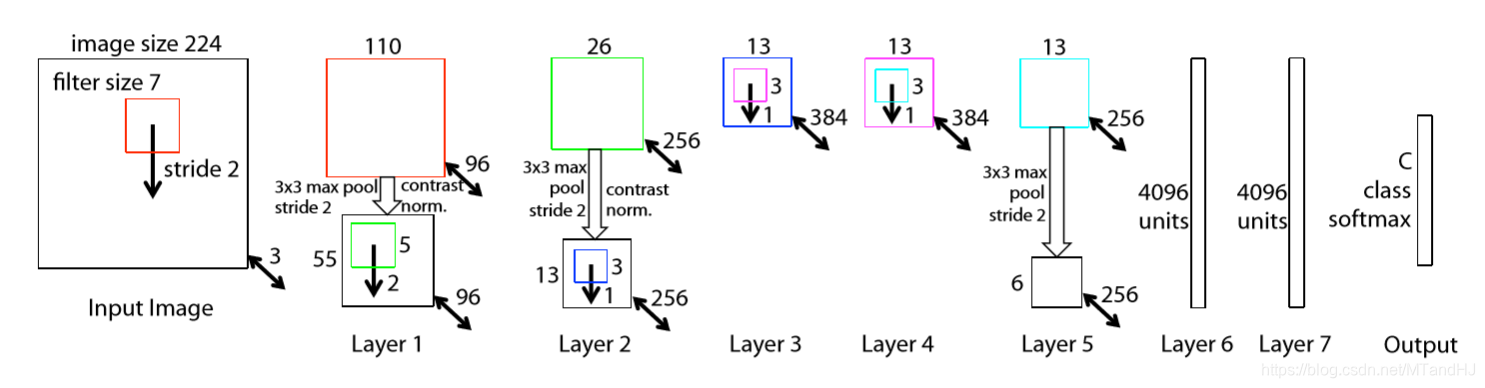
1. input: \(3 \times 224 \times 224\), filter size: 7, filter count: 96, stride: 2, padding: 1, 我觉得是要补一层零的，否则输出是109而不是110-->ReLU --> maxpool: size: \(3 \times 3\), stride: 2, 似乎这里也要补一层零， 否则 \(\lfloor \frac{110-3}{2}+1 \rfloor=54\) --> contrast normalized;
2. input: \(96 \times 55 \times 55\), filter size: 5, count: 256, stride: 2, padding: 0 --> ReLU --> maxpool: size: \(3 \times 3\), stride: 2, padding: 1--> contrast normlized;
3. input: \(256 \times 13 \times 13\), filter size: 3, count: 384, stride: 1, padding: 1 --> ReLU
4. input: \(384 \times 13 \times 13\), filter size: 3, count: 384, stride: 1, padding: 1 --> ReLU
5. input: \(384 \times 13 \times 13\), filter size: 3, count: 256, stride: 1, padding: 1 --> ReLU --> maxpool: size: 3, stride: 2, padding: 0 --> contrast normlized?
6. input: \(6 * 6 * 256\) -- > 4096 -- > ReLU -- > Dropout(0.5)
7. input: 4096 -- > 4096 --> ReLU -- > Dropout(0.5)
8. input: 4096 --> numclass ...

反卷积

网上看了很多人关于反卷积的解释，但是还是云里雾里的.

先关于步长为1的，不补零的简单情况进行分析吧, 假设:

input: \(i \times i\),

kernel_size: \(k \times k\) ,

stride: 1,

padding: 0

此时输出的大小\(o\)应当满足：

\[i = k + o - 1 \Rightarrow o = i-k+1
\]

现在，反卷积核大小依旧为\(k'=k\), 那么我们需要补零\(c'\)为多少才能使得反回去的特征大小为\(i\).

即:

\[2c' + o = k + i-1 \Rightarrow c'= k-1
\]

即我们要补零\(c'=k-1\).

如果stride 不为1呢？设为\(s\), 那么:

\[i = k + s(o-1) \Rightarrow o = \frac{i-k}{s}+1
\]

按照别的博客的说话，需要在特征之间插入零那么:

\[2c'+(s-1)(o-1) +o= k+s'(i-1)
\]

如果我们希望\(s'=1\)（至于为什么希望我不清楚）:

\[c' = k-1
\]

如果还有补零\(p\):

\[i+2p = k+s(o-1)
\]

但是回去的时候我们是不希望那个啥补零的，所以:

\[2c'+(s-1)(o-1) +o= k+s'(i-1)
\]

不变,

如果\(s'=1\), 结果为:

\[c' = k-p-1
\]

最大的问题是什么，是why! 为什么要这样反卷积啊？