AutoAssign源码分析

AutoAssign源码分析

一. 简介

关于动机和发展流程，原作者已经在知乎说的非常清楚，主要解决的问题总结如下：

联合各个loss（cls、reg、obj），这里前人已经做过很多
去除了centerness，这个东西非常难训练
去除了预定义的anchor匹配策略
去除FCOS类的不同FPN层解决不同尺度目标

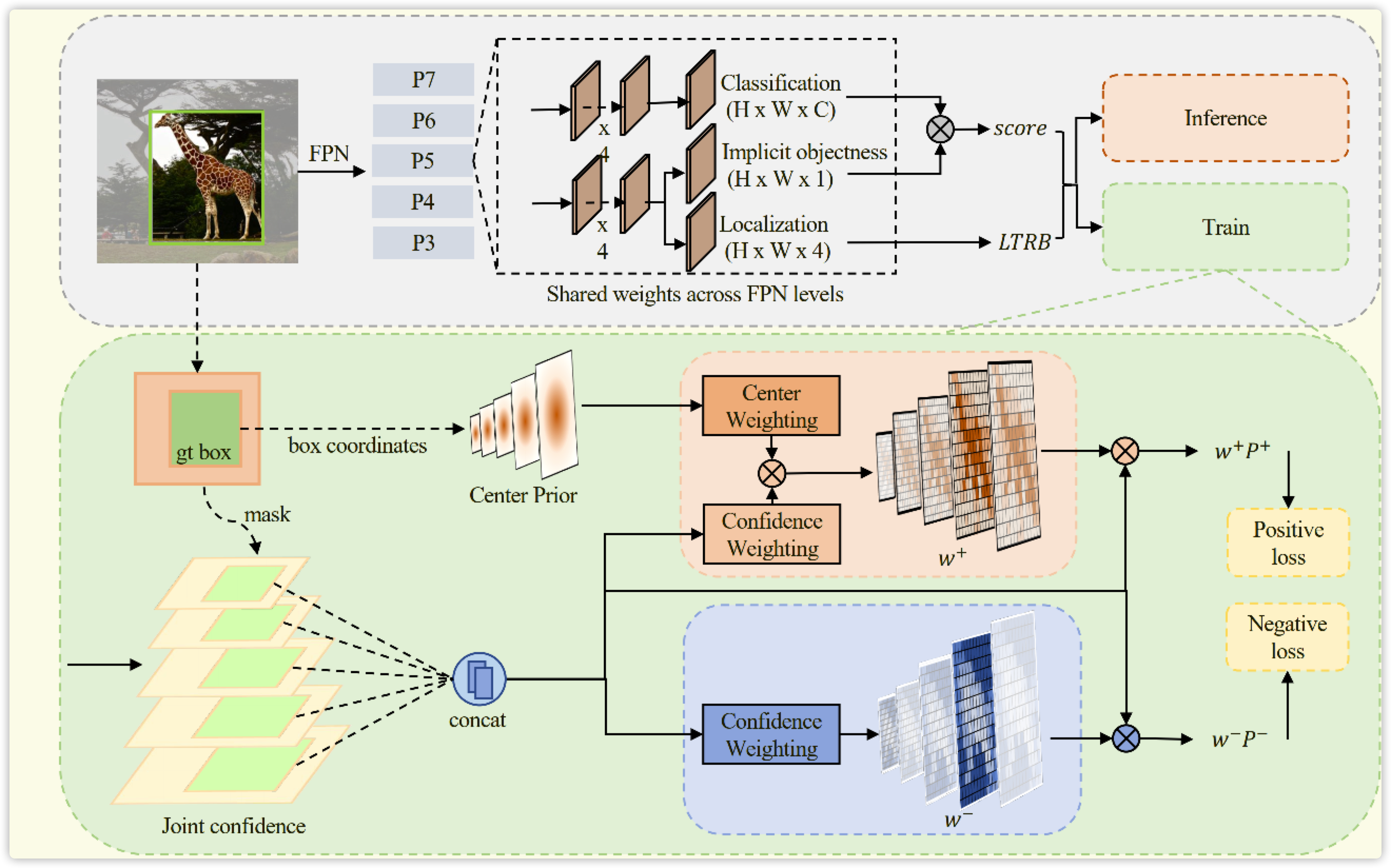
二. 论文理论

2.1 联合表示

为何进行联合表示？由于论文核心就是使用权重一词，而权重关系到 \(cls、reg、obj\) 等值大小，最后始终加权到一起。

论文引入 \(obj\) 参数（和YOLO的前背景类似，区别于centerness），未进行实际的监督，但效果在此处出奇的好，效果如下图所示。类似于一个 \(FCOS \ \ Scale\) 和一些不确定度论文的操作，直接获取一个可学习的 \(Weight\) 和目标进行相关操作。具体为何好，作者未给出实际的理论依据：

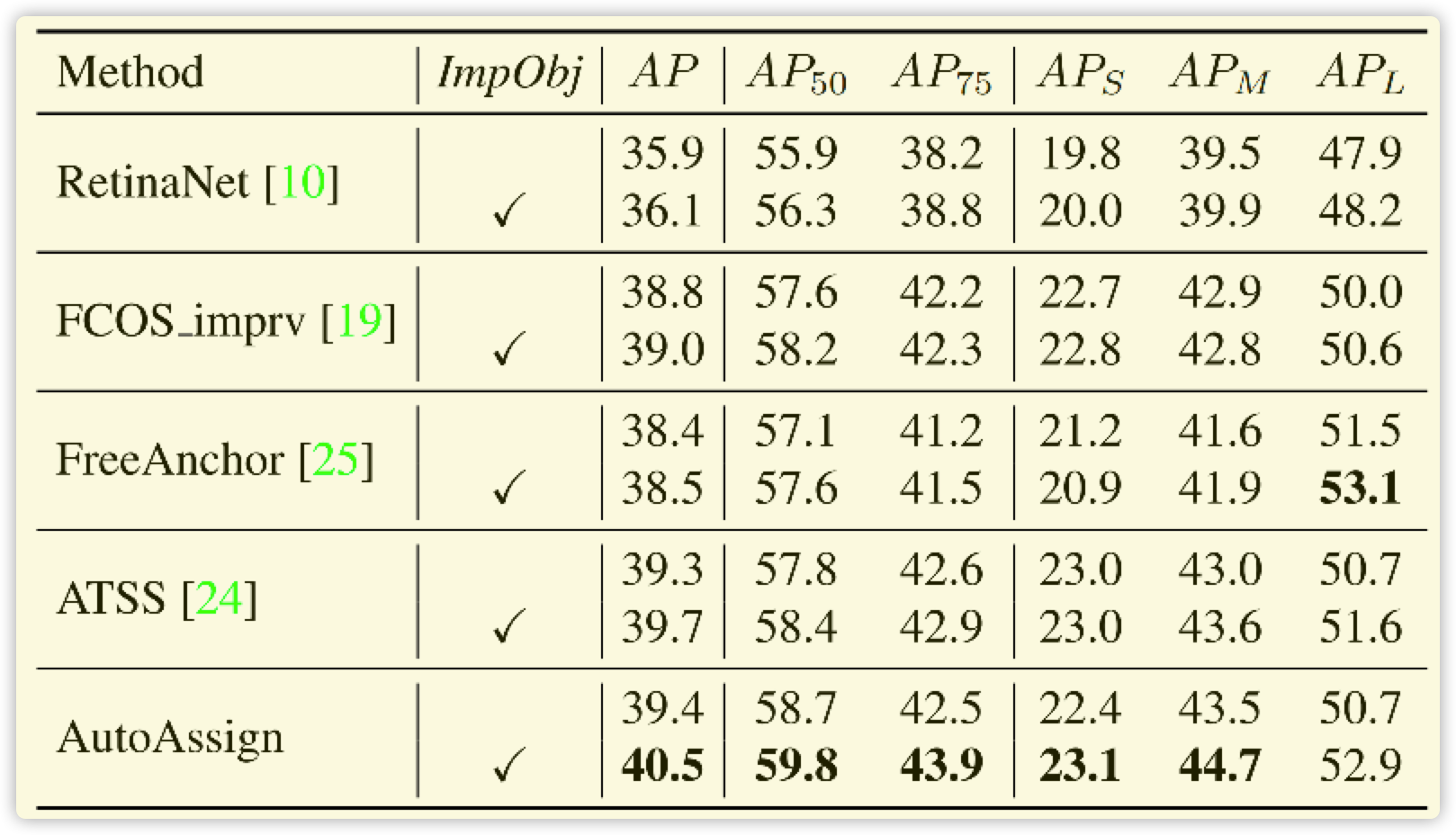
首先将 \(cls\) 和 \(obj\) 相乘进行融合，如下公式所示。注意：此处的 \(obj\) 是一个数，比如 \(batch=2,num_{cls}=80,anchor=100\) ，那么分类的结果为 \(2 \times100 \times 80\) ，但是 \(obj=2\times100\times1\) 。因为其表示的意思是：此 \(anchor\) 是前景还是背景。而具体的类别和置信度，全靠 \(cls\) 进行判断。

\[\mathcal{P}_{i}(\operatorname{cls} \mid \theta)=\mathcal{P}_{i}(\operatorname{cls} \mid o b j, \theta) \mathcal{P}_{i}(o b j \mid \theta)
\]

然后将 \(reg、cls\) 进一步联合表示，其中 \(L^{loc}\) 是计算的 \(IOU、GIOU、DIOU\) 结果，\(L^{cls}\) 是正样本的交叉熵 \(loss\) 。这也就和上面公式（1）对应起来，这里计算的都是正样本（此处表示GT内的anchor） \(loss\).

\[\begin{aligned}\mathcal{L}_{i}(\theta) &=\mathcal{L}_{i}^{c l s}(\theta)+\lambda \mathcal{L}_{i}^{l o c}(\theta) \\&=-\log \left(\mathcal{P}_{i}(\operatorname{cls} \mid \theta)\right)+\lambda \mathcal{L}_{i}^{l o c}(\theta) \\&=-\log \left(\mathcal{P}_{i}(c l s \mid \theta) e^{-\lambda \mathcal{L}_{i}^{l o c}(\theta)}\right) \\&=-\log \left(\mathcal{P}_{i}(c l s \mid \theta) \mathcal{P}_{i}(\operatorname{loc} \mid \theta)\right) \\&=-\log \left(\mathcal{P}_{i}(\theta)\right)\end{aligned}
\]

2.2 正样本权重

这里需要额外补充一点：GT内部的anchor包括正负样本，而GT外部肯定是负样本，这相当于人的先验。

2.1节中 \(L_i(\theta)\) 表示 \(Loss\) ，而内部的值 \(P_i(\theta)\) 就表示某个anchor为正样本的概率值，这个参考交叉熵正样本分类loss公式即可。所以 \(P_i(\theta)=P_i^{+}\) 也就是正样本的概率值（正样本的权重），下式（2）直接进行一个指数变换，相当于放大了正样本的置信度（概率=置信度），同时使用一个超参数进行调节放大倍数，这里其实没有太多其它意义。

\[C\left(\mathcal{P}_{i}^{+}\right)=e^{\mathcal{P}_{i}^{+} / \tau}
\]

\(G(d_i)\) 表示高斯权重，包括四组可学习参数: \(\mu->(x,y)\ 、\ \sigma->(x,y)\) ，每个种类四个参数，COCO数据集共 \(\sigma=80\times2,\mu=80\times2\). 那么公式（3）就很容易理解了，乘以权重以后取平均。其中可学习参数最重要的作用是防止初始化过拟合（参考了李翔知乎），如果没有高斯可学习参数，那么和正常anchor回归区别不大，假设A，B，C三个anchor，其中初始权重A>B>C，那么在下一轮的训练中依然是A>B>C，N轮之后A>>B>>C。这是一种强者越强的学习方式，完全陷入了和初始化息息相关的问题上了。而可学习的gaussian参数使得中心权重偏大，即使中心anchor初始化较差，后面也能慢慢学习加强，而偏远anchor会越来越差。

\[w_{i}^{+}=\frac{C\left(\mathcal{P}_{i}^{+}\right) G\left(\vec{d}_{i}\right)}{\sum_{j \in S_{n}} C\left(\mathcal{P}_{j}^{+}\right) G\left(\vec{d}_{j}\right)}
\]

正样本的Loss组成包括：\(cls、reg、obj\) ，发现上面的公式全部都已包含，直观上上理解是正确的。

2.3 负样本权重

负样本 \(loss\) 仅包含 \(cls、obj\) ，但是会参考 \(reg\) 的结果。前者不用多说，后者为什么会参考 \(reg\) 的值？因为回归的越好，是负样本的概率越低，正样本的loss会把正样本的 \(reg\) 学习的很好，而负样本的 \(reg\) 一直不学习就渐渐没落了。

\[f\left(\text { iou }_{i}\right)=1 /\left(1-\text { iou }_{i}\right)
\]

\[w_{i}^{-}=1-f\left(\text { iou }_{i}\right)
\]

负样本包含两个部分，在GT框之外的点全部都是负样本，在GT框之内的点IOU匹配度较差的点。GT框内点匹配度越差，那么负样本的权重越高，如上式（5）（6）所示。权重再乘以 \(\mathcal{P}_{i}(\operatorname{cls} \mid \theta)\) 就得到负样本的loss。

2.4 总的loss

按照2.3和2.4节的推导，很容易得出下式（6）的公式。但是正样本loss中的 \(\sum\) 有点不对称，按公式log完全可以拿到公式里面乘。按照李翔知乎里面说的，防止log的值太大无法收敛，这个地方笔者也没完全理解。

\[\mathcal{L}=-\sum_{n=1}^{N} \log \left(\sum_{i \in S_{n}} w_{i}^{+} \mathcal{P}_{i}^{+}\right)-\sum_{k \in S} \log \left(1-w_{k}^{-} \mathcal{P}_{k}^{-}\right)
\]

2.5 补充loss

看代码还有一个要点，每个GT框内anchor正样本权重gaussian-map得进行normlize，目的是让gaussian分布在anchor内部。

gaussian_norm_losses.append(

                len(gt_instances_per_image) / normal_probs[foreground_idxs].sum().clamp_(1e-12))  # gt数量/全部gaussian权重

'''

......

'''

loss_norm = torch.stack(gaussian_norm_losses).mean() * (1 - self.focal_loss_alpha)  # 期望让每个gt内的权重之和等于1（归一化过后容易学习）

三. 论文代码

注释代码地址：https://github.com/www516717402/AutoAssign

论文说的云里雾里，其实代码很简单，论文idea很好。

四. 总结

此论文肯定下了一番大功夫，细节地方挺多，比如公式（2），再比如加上 \(obj\) 参数。这些东西正常处理都不会加上，因为这篇论文核心就是去掉繁琐的操作，为什么还加上这个操作？那么答案肯定对此论文结果影响很大，论文图表已经证明这个猜想。
实际应用有点难推广
- 首先精度没有提升一个档次
- 论文中还是有很多提升细节不明朗
- 前向计算直接使用 \(obj\) 感觉有点不妥，没有直接进行监督有点后怕。。。
- 仅仅有一套gaussian参数（很多人质疑这一点，甜甜圈那种类型的结果如何？）
- 。。。

五. 参考