32、最长有效括号 | 算法（leetode，附思维导图 + 全部解法）300题

零 标题：算法（leetode，附思维导图 + 全部解法）300题之（32）最长有效括号

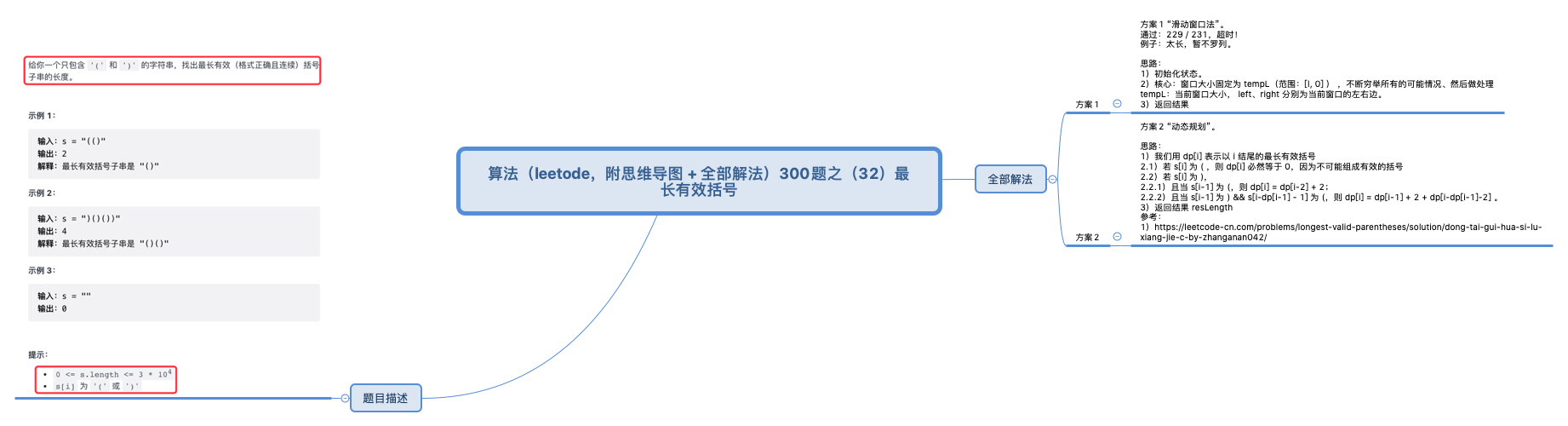
一 题目描述

二 解法总览（思维导图）

三 全部解法

1 方案1

1)代码：

// 方案1 “滑动窗口法”。
// 通过：229 / 231，超时！
// 例子：太长，暂不罗列。

// 思路：
// 1）初始化状态。
// 2）核心：窗口大小固定为 tempL（范围：[l, 0] ） ，不断穷举所有的可能情况、然后做处理
// tempL：当前窗口大小， left、right 分别为当前窗口的左右边。
// 3）返回结果
var longestValidParentheses = function(s) {
    // 判断当前子串 tempS 是否为 有效括号
    const isValidParentheses = (tempS = '') => {
        const l = tempS.length;
        let stack = [];

        for (let i = 0; i < l; i++) {
            if (tempS[i] === '(') {
                stack.push('(');
            }
            else {
                const tempChar = stack.pop();
                if (tempChar !== '(') {
                    return false;
                }
            }
        }

        return stack.length === 0;
    };

    // 1）初始化状态。
    const l = s.length;

    // 2）核心：窗口大小固定为 tempL（范围：[l, 0] ） ，不断穷举所有的可能情况、然后做处理
    // tempL：当前窗口大小， left、right 分别为当前窗口的左右边。
    for (let tempL = l; tempL > 0; tempL--) {
        // 优化：长度为奇数，肯定不是！
        if (tempL % 2 === 1) {
            continue;
        }

        for (let left = 0; left < (l - tempL + 1); left++) {
            const right = (left + tempL - 1);
            // 优化：最左、最右的字符一定分别是 '('、')' ！
            if (s[left] !== '(' || s[right] !== ')') {
                continue;
            }
            else {
                const tempS = s.slice(left, right + 1);
                if (isValidParentheses(tempS)) {
                    // 3）返回结果
                    return tempL;
                }
            }
        }
    }

    // 3.2）返回结果
    return 0;
};

2 方案2

1)代码：

// 方案2 “动态规划”。

// 思路：
// 1）我们用 dp[i] 表示以 i 结尾的最长有效括号
// 2.1）若 s[i] 为 ( ，则 dp[i] 必然等于 0，因为不可能组成有效的括号
// 2.2）若 s[i] 为 )，
// 2.2.1）且当 s[i-1] 为 (，则 dp[i] = dp[i-2] + 2；
// 2.2.2）且当 s[i-1] 为 ) && s[i-dp[i-1] - 1] 为 (，则 dp[i] = dp[i-1] + 2 + dp[i-dp[i-1]-2] 。
// 3）返回结果 resLength
// 参考：
// 1）https://leetcode-cn.com/problems/longest-valid-parentheses/solution/dong-tai-gui-hua-si-lu-xiang-jie-c-by-zhanganan042/
var longestValidParentheses = function(s) {
    // 1）状态初始化
    const l = s.length;
    let dp = Array(l).fill(0),
        resLength = 0;

    // 2）核心：
    // 1）我们用 dp[i] 表示以 i 结尾的最长有效括号
    // 2.1）若 s[i] 为 ( ，则 dp[i] 必然等于 0，因为不可能组成有效的括号
    // 2.2）若 s[i] 为 )，
    // 2.2.1）且当 s[i-1] 为 (，则 dp[i] = dp[i-2] + 2；
    // 2.2.2）且当 s[i-1] 为 ) && s[i-dp[i-1] - 1] 为 (，则 dp[i] = dp[i-1] + 2 + dp[i-dp[i-1]-2] 。
    for (let i = 0; i < l; i++) {
        if (i > 0 && s[i] === ')') {
            if (s[i - 1] === '(') {
                dp[i] = ((i - 2 >= 0) ? dp[i - 2] + 2 : 2);
            }
            else if (s[i - 1] === ')' && (i - dp[i - 1] - 1 >= 0) && (s[i- dp[i - 1] - 1] === '(')) {
                dp[i] = dp[i - 1] + 2 + (i - dp[i - 1] - 2 >= 0 ? dp[i - dp[i - 1] - 2] : 0);
            }
        }
        resLength = Math.max(resLength, dp[i]);
    }

    // 3）返回结果 resLength
    return resLength;
}