SpringIOC 理论推导

IOC理论实现

1. UserDao接口

public interface UserDao {
    void say();
}

1. UserDaoImpl实现类

public class UserDaoImpl implements UserDao {
    public void say() {
        System.out.println("我想使用默认数据库");
    }
}

1. UserService接口

public interface UserService {
    void say();
}

1. UserServiceImpl实现类
   
   

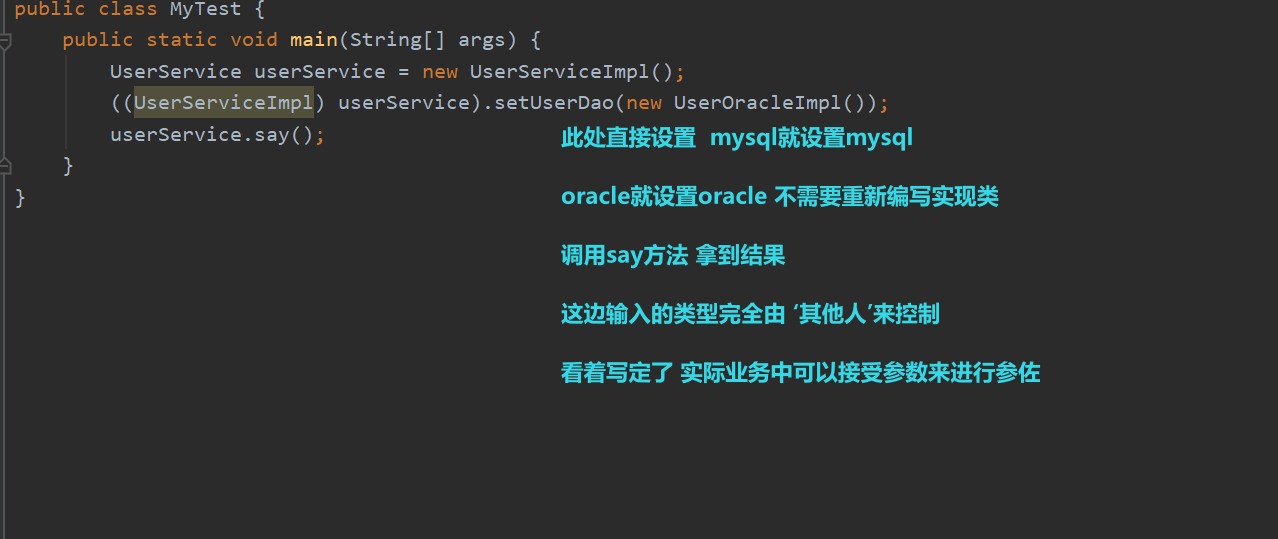
如以上代码 如果当前业务跟代码逻辑一样 没有任何问题 输出 我想使用默认数据库

---

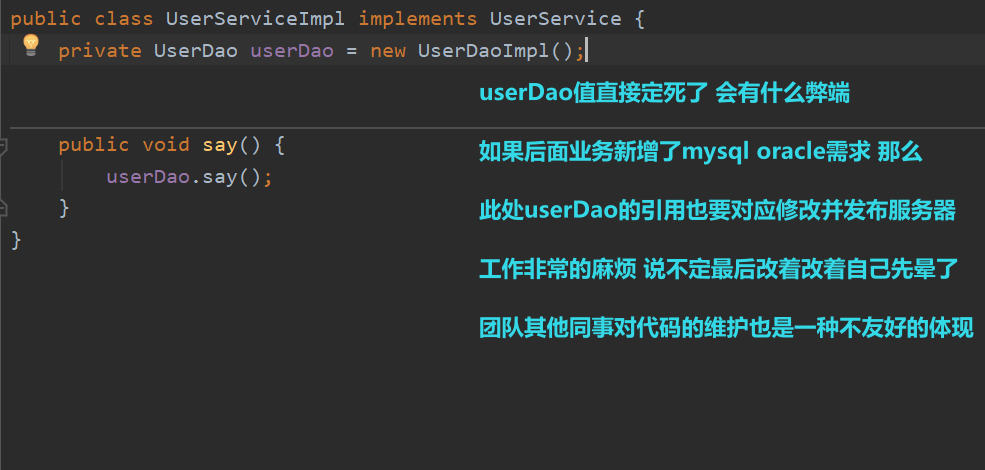
如果后面有需求 我想使用MySQL数据库Oracle数据库等等 有一种方法 service实现类多写几个 实现MySQL数据库Oracle数据库 再调用对应的接口即可 如果有成千上万个类似的需求 是不是要写成千上万个？还有一种 将userDao的引用指向业务想要的 那么如果频繁修改 业务逻辑代码也能相对应的改 麻烦不说 且还容易出问题

---

所以 为了解决工作不便 需要转变一下思路 能不能让private UserDao userDao动态化 就像我是mysql userDao就是Mysql 我是oracle userDao就是oracle

---

新增MySQL Oracle业务

public class UserMysqlImpl implements UserDao {
    public void say() {
        System.out.println("我想使用Mysql数据库");
    }
}

public class UserOracleImpl implements UserDao {
    public void say() {
        System.out.println("我想使用oracle数据库");
    }
}

---

测试

如图所示 就是这样一个改动 加了一个set方法 整个代码逻辑就变得很清楚 需求是什么 我们就传入什么

以前userDao的控制完全在程序本身 设置的什么 就是什么 没有可扩展性

---

现在对象的创建或者说需求的实现发生了反转 程序被动的接收userDao的值 程序不需要知道userDao什么时候创建的 什么时候传入进来的 只需要把最终的结果返回出来就好了

---

IOC控制反转 控制什么反转了? 创建对象的控制权反转了 以前创建对象的主动权和创建时机由程序把握 现在这种权力反转给其他方了