day6 斐波那契数列
1、求图片中的表达式:
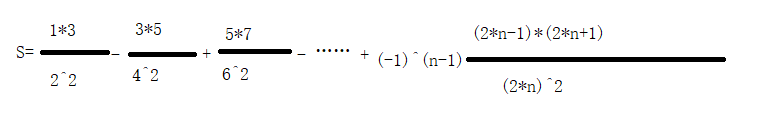
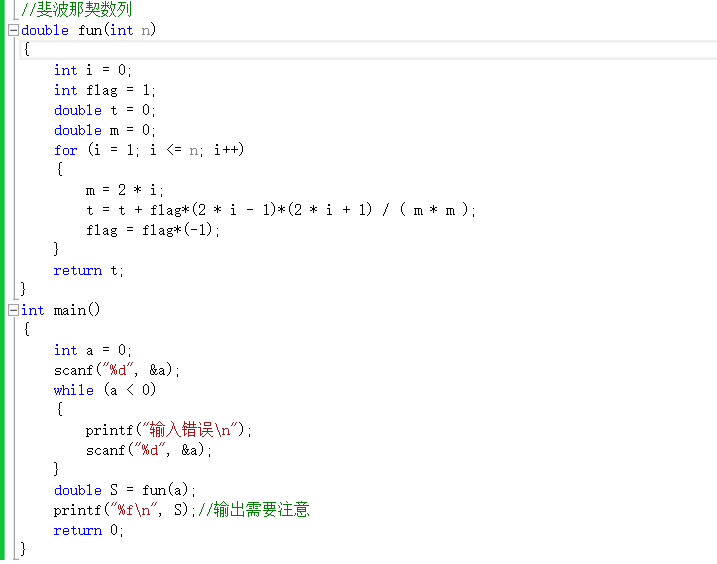

2、求图中斐波那契数列的值
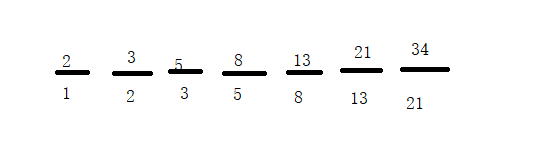
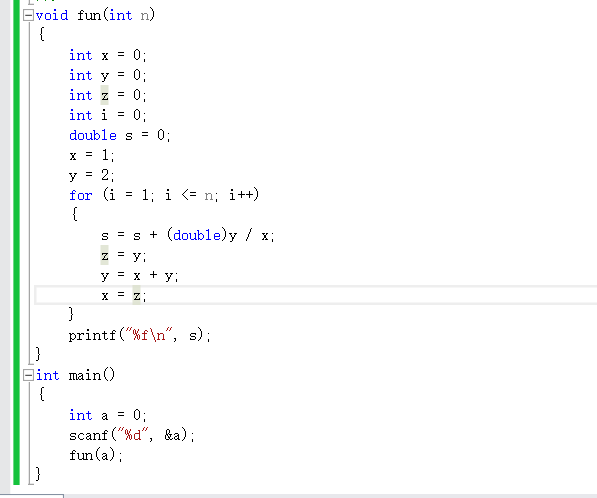
day6 斐波那契数列的更多相关文章
- C#求斐波那契数列第30项的值(递归和非递归)
using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.T ...
- 斐波拉契数列加强版——时间复杂度O(1),空间复杂度O(1)
对于斐波拉契经典问题,我们都非常熟悉,通过递推公式F(n) = F(n - ) + F(n - ),我们可以在线性时间内求出第n项F(n),现在考虑斐波拉契的加强版,我们要求的项数n的范围为int范围 ...
- js中的斐波那契数列法
//斐波那契数列:1,2,3,5,8,13…… //从第3个起的第n个等于前两个之和 //解法1: var n1 = 1,n2 = 2; for(var i=3;i<101;i++){ var ...
- 剑指Offer面试题:8.斐波那契数列
一.题目:斐波那契数列 题目:写一个函数,输入n,求斐波那契(Fibonacci)数列的第n项.斐波那契数列的定义如下: 二.效率很低的解法 很多C/C++/C#/Java语言教科书在讲述递归函数的时 ...
- 算法: 斐波那契数列C/C++实现
斐波那契数列: 1,1,2,3,5,8,13,21,34,.... //求斐波那契数列第n项的值 //1,1,2,3,5,8,13,21,34... //1.递归: //缺点:当n过大时,递归 ...
- 洛谷P1962 斐波那契数列 || P1349 广义斐波那契数列[矩阵乘法]
P1962 斐波那契数列 大家都知道,斐波那契数列是满足如下性质的一个数列: • f(1) = 1 • f(2) = 1 • f(n) = f(n-1) + f(n-2) (n ≥ 2 且 n 为整数 ...
- Python递归及斐波那契数列
递归函数 在函数内部,可以调用其他函数.如果一个函数在内部调用自身本身,这个函数就是递归函数.举个例子,我们来计算阶乘 n! = 1 * 2 * 3 * ... * n,用函数 fact(n)表示,可 ...
- 简单Java算法程序实现!斐波那契数列函数~
java编程基础--斐波那契数列 问题描述:一只青蛙一次可以跳上1级台阶,也可以跳上2级.求该青蛙跳上一个n级的台阶总共有多少种跳法. 思路:可能出现的情况:(1) n=1 ,一种方法 ;(2)n=2 ...
- js 斐波那契数列(兔子问题)
对于JS初学者来说,斐波那契数列一直是个头疼的问题,总是理不清思路. 希望看完这篇文章之后会对你有帮助. 什么是斐波那契数列 : 答: 斐波那契数列,又称黄金分割数列.因数学家列昂纳多·斐波那契(Le ...
随机推荐
- 数据库函数(Excel函数集团)
此处文章均为本妖原创,供下载.学习.探讨! 文章下载源是Office365国内版1Driver,如有链接问题请联系我. 请勿用于商业! 谢谢 下载地址:https://officecommunity- ...
- Google Earth Engine 中的位运算
Google Earth Engine中的位运算 按位运算是编程中一个难点,同时也是在我们后续处理影像数据,尤其要使用影像自带的波段比如QA波段经常会用到的一个东西.通过按位运算我们可以筛选出我们想要 ...
- 微前端框架 qiankun 技术分析
我们在single-spa 技术分析 基本实现了一个微前端框架需要具备的各种功能,但是又实现的不够彻底,遗留了很多问题需要解决.虽然官方提供了很多样例和最佳实践,但是总显得过于单薄,总给人一种&quo ...
- Excel数据导出功能
HTML代码: <a id="aExportData" hidden><span>Export</span></a> <div ...
- Git差异并列显示
默认的git diff命令只会将文件的修改差异使用"+","-"符号标注出来,并不直观. 最理想的方式应该是使用诸如"DiffMerge"这 ...
- Sharepoint 恢复列表文件
当在Sharepoint中恢复列表字段,列表数据时,恢复的是stp文件,可按照如下步骤恢复: 1.打开http://liuqiang17-1/sites/flsharepoint/_catalogs/ ...
- C++ 11新特性:std::future & std::shared_future) (转载)
上一讲<C++11 并发指南四(<future> 详解二 std::packaged_task 介绍)>主要介绍了 <future> 头文件中的 std::pack ...
- Linux(centos7)安装redis并设置redis开机自启动
1.下载redis安装包 wget http://download.redis.io/releases/redis-4.0.6.tar.gz 2.解压安装包 tar -zxvf redis-4.0.6 ...
- 🍃【Spring专题】「原理系列」SpringMVC的运行工作原理(补充修订)
承接相关之前的SpringMVC的框架技术的流程分析 初始化流程(initStrategies) 执行流程 寻找相关HandlerMapping 请求到DispatcherServlet类进行执行相关 ...
- 【LeetCode】794. Valid Tic-Tac-Toe State 解题报告(Python)
作者: 负雪明烛 id: fuxuemingzhu 个人博客: http://fuxuemingzhu.cn/ 题目地址: https://leetcode.com/problems/valid-ti ...
