小谈C#泛型

（一）泛型的由来

泛型是CLR2.0新增的，泛型兼具可重用性，类型安全和效率。泛型的本质就是在程序第一次编译的为IL代码的时候，就会帮我们生成一个占位符，在git即时编译的时候，就会把占位符替换为真实的类型。

泛型的语法很简单，也没啥好说的。在我们编程中，经常碰到逻辑非常相似的模块，但是参数不一样的情况，这个时候就要考虑用到泛型。

（二）泛型的种类

1、泛型方法

2、泛型类

3、泛型接口

4、泛型委托

这里顺带提一下，泛型类和泛型接口的继承问题，大家可以自己尝试一下。

（三）泛型约束

有约束才有自由，有权利才有义务；

1、基类约束

2、接口约束

3、New()

4、引用类型约束(Class 约束)

5、值类型约束(Struct约束)

这里需要特别注明：泛型方法的返回值的问题，用default(T)

（四）协变，逆变

下面来说说，今天的重点，协变和逆变。

基本概念：out 关键字是用来协变的，in关键字是用来逆变的，协变和逆变只发生在泛型接口和泛型委托上面。

下面直接上代码，首先定义了两个类，一个是鸟类，一个是麻雀类，麻雀类继承自鸟类。

    public class Bird
    {
        public int Id { get; set; }
    }

    public class Sparrow:Bird
    {
        public string Name { get; set;  }
    }

下面是简单里氏替换原则，相信大家都能理解；

             Bird bird=new Bird();
            //这个不会报错，里氏替换原则
             Bird sparrow=new Sparrow();
            //下面这种做法会报错
            //Sparrow sparrow2=new Bird();

再到下面这种情况

            List<Bird> birdList1=new List<Bird>();
            //这个会报错，这个意思就是一群麻雀，等于一群鸟，在我们自己的逻辑上是没有问题的
            //但是程序呢，只认父子关系，两个List之间没有父子关系。
            //List<Bird> birdList2=new List<Sparrow>();
            //使用下面这个方法转换一下就好了。
            List<Bird> birdList2 = new List<Sparrow>().Select(d=>(Bird)d).ToList();

微软为了解决上面这种情况，在我们自己的逻辑上认为，一群麻雀肯定是一群鸟的，所以就引入了协变这个概念。协变呢，在我们平时自己编程中，确实很少用到，但是在微软的框架里面却经常看到，连最常见的IEnumerable接口是支持协变的，看定义如下：

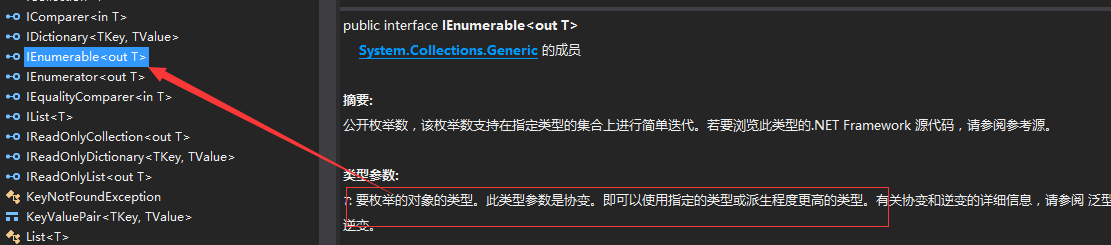
所以刚刚那个例子可以这么写：

            IEnumerable<Bird> birds = new List<Sparrow>();
            //这个协变呢，声明都是基于基类的，让我们的面向抽象的编程变得更加彻底。
            //微软自己给自己打的补丁。
            //其实虽然这个是协变，内部还是帮我们像上面一样，进行了类型转换，只不过这个过程是微软自己帮我们做了。
            //还要特别说明一点协变，只能是返回结果。

  public interface IMyList<out T>{

    }

    public class MyList<T>:IMyList<T>{

    }

第二个是自己写的支持协变的做法。

协变的内容大概就是这么多了，下面来讲讲逆变，逆变和协变刚好相反，是声明派生类，然后用父类来赋值，这个就有点感觉像违法我们的面向对象的感觉。

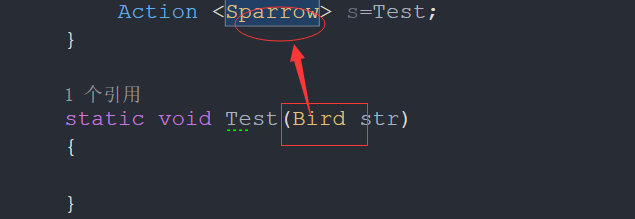
上面这种就叫做逆变。逆变就是把父类反转赋值给子类。

其实.net framework里面很多关于协变，逆变的，尽管我们可能自己写代码用不到，但是我们也应该要了解和学习。