【树形DP】洛谷P1352_没有上司的舞会

本人第一篇Blog,初学树形DP,心情别样鸡冻...

好了废话不多说,我们来看看题目[传送门]

---

某大学有N个职员，编号为1~N。他们之间有从属关系，也就是说他们的关系就像一棵以校长为根的树，父结点就是子结点的直接上司。现在有个周年庆宴会，宴会每邀请来一个职员都会增加一定的快乐指数Ri，但是呢，如果某个职员的上司来参加舞会了，那么这个职员就无论如何也不肯来参加舞会了。所以，请你编程计算，邀请哪些职员可以使快乐指数最大，求最大的快乐指数。

输入输出格式

输入格式：

第一行一个整数N。(1<=N<=6000)

接下来N行，第i+1行表示i号职员的快乐指数Ri。(-128<=Ri<=127)

接下来N-1行，每行输入一对整数L,K。表示K是L的直接上司。

最后一行输入0 0

 输出格式：

输出最大的快乐指数。

样例输入：

7
1
1
1
1
1
1
1
1 3
2 3
6 4
7 4
4 5
3 5
0 0

样例输出：

5

---

菜到真实,以泪洗面QAQ

这是一道很经典的树形DP题目,相信我(其实是自己太菜233)

首先我们应该确定一个状态emmm.....

我们以 f[u][1] 表示u号员工回去参加舞会时他的非直属员工的最大快乐值 亚索：我听到有人在呼唤我

相对的 f[u][0] 则表示u号员工没有去的最大快乐值。

很容易就可以得到答案便是max(f[root][1],f[root][0])大老板我劝你善良

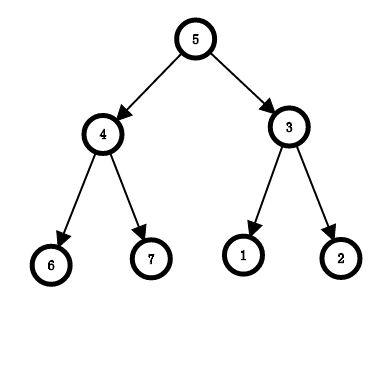
可以看出每个人和上司之间是可以连一条边的,那么很容易得到下面的一颗树(注意，这里是单向边，因为需要表示上司和部下的关系)

[好用的图论绘图网页你值得拥有]

可以看出5号节点是根节点(记住，在有向图里面这很重要！！！无向图是可以任选一个点作为根节点)，那么怎么找到这颗树的根节点呢？？？

很简单:一个flag标记和读完后一个循环扫描，原理是因为在无向图中根节点是不可能有任何父亲。

  for(int i=;i<n;++i) scanf("%d%d",&a,&b),add(b,a),flag[a]==true?:flag[a]=true;//这个地方比较坑的就是存边是b是a的父亲。。。
  for(int i=;i<=n;++i) if(!flag[i]) root=i;

好了现在是重头戏——DP部分。。。

思想非常简单，和一般树形DP基本一样

先枚举边，再把边给递归传下去emmm

 void dp(int u)
 {
     for(int i=head[u];i!=-;i=edge[i].nxt)
     {
         int v=edge[i].to;
         dp(v);
         f[u][]+=max(f[v][],f[v][]);
         f[u][]+=f[v][];
     }
     f[u][]+=h[u];
 }

所以,下面给出完整代码:

 #include<bits/stdc++.h>
 namespace Jason{
     inline void scan(int &x){
     int f=;x=;char s=getchar();
     while(s<'' || s>''){if(s=='-') f=-;s=getchar();}
     while(s>='' && s<=''){x=x*+s-'';s=getchar();}
     x*=f;
 }
     inline void print(int x){
         if(x<){putchar('-');x=-x;}
         if(x>)print(x/);char s=x%+'';
         putchar(s);
     }
 }
 using namespace std;
 using namespace Jason;
 const int maxn=+;
 //---------------------以下是数据结构
 int n,cnt=;
 struct Edge{
     int to,nxt;//这里用nxt是因为在C++11里面std已经有next了
 }edge[maxn<<];int head[maxn];
 int h[maxn];
 bool flag[maxn];
 int f[maxn][];
 //----------------------
 void add(int u,int v){
     edge[++cnt].nxt=head[u];
     edge[cnt].to=v;
     head[u]=cnt;
 }

 void dp(int u)
 {
     for(int i=head[u];i!=-;i=edge[i].nxt)
     {
         int v=edge[i].to;
         dp(v);
         f[u][]+=max(f[v][],f[v][]);
         f[u][]+=f[v][];
     }
     f[u][]+=h[u];
 }
 int main(int arrc,char *arrv[])
 {
     //freopen("in","r",stdin);
     memset(head,-,sizeof(head));
     int a,b,root;
     scan(n);
     for(int i=;i<=n;++i) scan(h[i]);
     for(int i=;i<n;++i) scan(a),scan(b),add(b,a),flag[a]==true?:flag[a]=true;
     scan(a),scan(b);
     for(int i=;i<=n;++i) if(!flag[i]) root=i;//找根节点，因为根节点不可能是任意一个点的儿子
     dp(root);
     print(max(f[root][],f[root][]));
     return ;
 }

orz欢迎大佬踩我QwQ。。。