机器学习入门学习笔记：（一）BP神经网络原理推导及程序实现

　　机器学习中，神经网络算法可以说是当下使用的最广泛的算法。神经网络的结构模仿自生物神经网络，生物神经网络中的每个神经元与其他神经元相连，当它“兴奋”时，想下一级相连的神经元发送化学物质，改变这些神经元的电位；如果某神经元的电位超过一个阈值，则被激活，否则不被激活。误差逆传播算法（error back propagation）是神经网络中最有代表性的算法，也是使用最多的算法之一。

误差逆传播算法理论推导

　　误差逆传播算法（error back propagation）简称BP网络算法。而一般在说BP网络算法时，默认指用BP算法训练的多层前馈神经网络。

　　下面是一个简单的BP神经网络示意图。其拥有一个输入层，一个隐含层，一个输出层。推导中采用这种简单的三层的神经网络。

　　定义相关的一些变量如下：

1. 假设有 d 个输入神经元，有 l 个输出神经元，q 个隐含层神经元；
2. 设输出层第 j 个神经元的阈值为 θ_j ；
3. 设隐含层第 h 个神经元的阈值为 γ_h ；
4. 输入层第 i 个神经元与隐含层第 h 个神经元之间的连接权为 V_ih ；
5. 隐含层第 h 个神经元与输出层第 j 个神经元之间的连接权为 W_hj ；
6. 记隐含层第 h 个神经元接收到来自于输入层的输入为 α_h：

   　

7. 记输出层第 j 个神经元接收到来自于隐含层的输入为 β_j：

　　　　　　　　　　　　　，其中 b_h 为隐含层第 h 个神经元的输出

　　理论推导：

　　在神经网络中，神经元接收到来自来自其他神经元的输入信号，这些信号乘以权重累加到神经元接收的总输入值上，随后与当前神经元的阈值进行比较，然后通过激活函数处理，产生神经元的输出。

　　激活函数：

　　理想的激活函数是阶跃函数，“0”对应神经元抑制，“1”对应神经元兴奋。然而阶跃函数的缺点是不连续，不可导，且不光滑，所以常用sigmoid函数作为激活函数代替阶跃函数。如下图分别是阶跃函数和sigmoid函数。

　　阶跃函数：

　　sigmoid函数：

　　对于一个训练例（x_k, y_k），假设神经网络的输出为 Y_k ，则输出可表示为：

　　　　

f(***)表示激活函数，默认全部的激活函数都为sigmoid函数。

　　则可以计算网络上，（x_k, y_k）的均方差误差为：

　　　　

　　乘以1/2是为了求导时能正好抵消掉常数系数。

　　现在，从隐含层的第h个神经元看，输入层总共有 d 个权重传递参数传给他，它又总共有 l 个权重传递参数传给输出层, 自身还有 1 个阈值。所以在我们这个神经网络中，一个隐含层神经元有（d+l+1）个参数待确定。输出层每个神经元还有一个阈值，所以总共有 l 个阈值。最后，总共有（d+l+1）*q+l 个待定参数。

首先，随机给出这些待定的参数，后面通过BP算法的迭代，这些参数的值会逐渐收敛于合适的值，那时，神经网络也就训练完成了。

　　任意权重参数的更新公式为：

　　　　

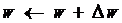
　　下面以隐含层到输出层的权重参数 w_hj 为例说明：

　　我们可以按照前面给出的公式求出均方差误差 E_k ，期望其为0，或者为最小值。而BP算法基于梯度下降法（gradient descent）来求解最优解，以目标的负梯度方向对参数进行调整，通过多次迭代，新的权重参数会逐渐趋近于最优解。对于误差 E_k ，给定学习率（learning rate）即步长 η ，有：

　　　　

　　再看一下参数的传递方向，首先 w_hj 影响到了输出层神经元的输入值 β_j ，然后影响到输出值 Y_j^k ,然后再影响到误差 E_k ，所以可以列出如下关系式：

　　　　

　　根据输出层神经元的输入值 β_j 的定义：

　　　　

　　得到：

　　　　

　　对于激活函数（sigmoid函数）：

　　　　

　　很容易通过求导证得下面的性质：

　　　　

　　使用这个性质进行如下推导：

　　令：

　　　　

　　又由于：

　　　　

　　所以：

　　　　 

　　由前面的定义有：

　　　　

　　所以：

　　　　

　　把这个结果结合前面的几个式子代入：

　　　　，  ，  

　　得到：

　　　　

　　所以：

　　　　

　　OK，上面这个式子就是梯度了。通过不停地更新即梯度下降法就可实现权重更新了。

　　　　

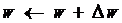
　　推导到这里就结束了，再来解释一下式子中各个元素的意义。

　　　　

　　η 为学习率，即梯度下降的补偿；为神经网络输出层第 j 个神经元的输出值；为给出的训练例（x_k, y_k）的标志（label），即训练集给出的正确输出；为隐含层第 h 个神经元的输出。

　　

　　类似可得：

　　　　

　　其中，

　　　　

　　这部分的解法与前面的推导方法类似，不做赘述。

　　接下来是代码部分：

　　这段代码网上也有不少地方可以看到，后面会简单介绍一下程序。

　　完整程序：文件名“NN_Test.py”

# _*_ coding: utf-8 _*_

import numpy as np

def tanh(x):
    return np.tanh(x)

def tanh_derivative(x):
    return 1 -  np.tanh(x) * np.tanh(x)

# sigmod函数
def logistic(x):
    return 1 / (1 + np.exp(-x))

# sigmod函数的导数
def logistic_derivative(x):
    return logistic(x) * (1 - logistic(x))

class NeuralNetwork:
    def __init__ (self, layers, activation = 'tanh'):
        if activation == 'logistic':
            self.activation = logistic
            self.activation_deriv = logistic_derivative
        elif activation == 'tanh':
            self.activation = tanh
            self.activation_deriv = tanh_derivative

        # 随机产生权重值
        self.weights = []
        for i in range(1, len(layers) - 1):     # 不算输入层，循环
            self.weights.append((2 * np.random.random( (layers[i-1] + 1, layers[i] + 1)) - 1) * 0.25 )
            self.weights.append((2 * np.random.random( (layers[i] + 1, layers[i+1])) - 1) * 0.25 )
            #print self.weights

    def fit(self, x, y, learning_rate=0.2, epochs=10000):
        x = np.atleast_2d(x)
        temp = np.ones([x.shape[0], x.shape[1]+1])
        temp[:, 0:-1] = x
        x = temp
        y = np.array(y)

        for k in range(epochs): # 循环epochs次
            i = np.random.randint(x.shape[0])   # 随机产生一个数，对应行号，即数据集编号
            a = [x[i]]  # 抽出这行的数据集

            # 迭代将输出数据更新在a的最后一行
            for l in range(len(self.weights)):
                a.append(self.activation(np.dot(a[l], self.weights[l])))

            # 减去最后更新的数据，得到误差
            error = y[i] - a[-1]
            deltas = [error * self.activation_deriv(a[-1])]

            # 求梯度
            for l in range(len(a) - 2, 0, -1):
                deltas.append(deltas[-1].dot(self.weights[l].T) * self.activation_deriv(a[l]) )

            #反向排序
            deltas.reverse()   

           # 梯度下降法更新权值
            for i in range(len(self.weights)):
                layer = np.atleast_2d(a[i])
                delta = np.atleast_2d(deltas[i])
                self.weights[i] += learning_rate * layer.T.dot(delta)

    def predict(self, x):
        x = np.array(x)
        temp = np.ones(x.shape[0] + 1)
        temp[0:-1] = x
        a = temp
        for l in range(0, len(self.weights)):
            a = self.activation(np.dot(a, self.weights[l]))
        return a     

简要说明：

def tanh(x):
    return np.tanh(x)

def tanh_derivative(x):
    return 1 -  np.tanh(x) * np.tanh(x)

# sigmod函数
def logistic(x):
    return 1 / (1 + np.exp(-x))

# sigmod函数的导数
def logistic_derivative(x):
    return logistic(x) * (1 - logistic(x))

分别表示两种激活函数，tanh函数和sigmoid函数以及其的导数，有关激活函数前文有提及。

        if activation == 'logistic':
            self.activation = logistic
            self.activation_deriv = logistic_derivative
        elif activation == 'tanh':
            self.activation = tanh
            self.activation_deriv = tanh_derivative

“activation”参数决定了激活函数的种类，是tanh函数还是sigmoid函数。

　　　　 self.weights = []
        for i in range(1, len(layers) - 1):     # 不算输入层，循环
            self.weights.append((2 * np.random.random( (layers[i-1] + 1, layers[i] + 1)) - 1) * 0.25 )
            self.weights.append((2 * np.random.random( (layers[i] + 1, layers[i+1])) - 1) * 0.25 )
            #print self.weights    

以隐含层前后层计算产生权重参数，参数初始时随机，取值范围是[-0.25, 0.25]

        x = np.atleast_2d(x)
        temp = np.ones([x.shape[0], x.shape[1]+1])
        temp[:, 0:-1] = x
        x = temp
        y = np.array(y)

创建并初始化要使用的变量。

for k in range(epochs): # 循环epochs次
            i = np.random.randint(x.shape[0])   # 随机产生一个数，对应行号，即数据集编号
            a = [x[i]]  # 抽出这行的数据集

            # 迭代将输出数据更新在a的最后一行
            for l in range(len(self.weights)):
                a.append(self.activation(np.dot(a[l], self.weights[l])))

            # 减去最后更新的数据，得到误差
            error = y[i] - a[-1]
            deltas = [error * self.activation_deriv(a[-1])]

            # 求梯度
            for l in range(len(a) - 2, 0, -1):
                deltas.append(deltas[-1].dot(self.weights[l].T) * self.activation_deriv(a[l]) )

            #反向排序
            deltas.reverse()   

           # 梯度下降法更新权值
            for i in range(len(self.weights)):
                layer = np.atleast_2d(a[i])
                delta = np.atleast_2d(deltas[i])
                self.weights[i] += learning_rate * layer.T.dot(delta)

进行BP神经网络的训练的核心部分，在代码中有相应注释。

    def predict(self, x):
        x = np.array(x)
        temp = np.ones(x.shape[0] + 1)
        temp[0:-1] = x
        a = temp
        for l in range(0, len(self.weights)):
            a = self.activation(np.dot(a, self.weights[l]))
        return a     

这段是预测函数，其实就是将测试集的数据输入，然后正向走一遍训练好的网络最后再返回预测结果。

测试验证函数：

# _*_ coding: utf-8 _*_

from NN_Test import NeuralNetwork
import numpy as np

nn = NeuralNetwork([2, 2, 1], 'tanh')
x = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y = np.array([0, 1, 1, 0])
nn.fit(x, y)
for i in [[0, 0], [0, 1], [1, 0], [1, 1]]:
    print(i, nn.predict(i))

程序中测试的是异或关系，下面是运行结果：

([0, 0], array([-0.01628435]))
([0, 1], array([ 0.99808061]))
([1, 0], array([ 0.99808725]))
([1, 1], array([-0.03867579]))

显然与标准异或关系近似。