<泛> 多路快排

今天写一个多路快排函数模板，与STL容器兼容的。

我们默认为升序排序

因为，STL容器均为逾尾容器，所以我们这里采用的参数也是逾尾的参数

一、二路快排

基本思路

给你一个序列，先选择一个数作为基数，我们要做的是把小于该基数的数字放于左侧，大于该基数的数字放于右侧，最后将此基数放于中间，形成新的序列，我们把左侧序列和右侧序列分别像之前那样做，最后得到的序列即为顺序序列。

过程演示

比如给你一个序列   4  3  1  5  4  7  9  1  8  0

我们采用双指针扫描法，红色代表左指针所指位置，绿色代表右指针所指位置

我们选取一个数作为基数，假设选第一个数，即 flag  为  4

那么，我们把这个位置空出来，用null表示

则，一开始的序列图为

null  3  1  5  4  7  9  1  8  0                 flag  is  4

我们从右指针开始遍历，找到第一个小于flag的数字，填入坑中，然后左指针++，指向下一位然后开始遍历

0    1  5  4  7  9  1  8  null                

0  3    5  4  7  9  1  8  null         

0  3  1    4  7  9  1  8  null    

0  3  1  null  4  7  9  1    5  

0  3  1  null  4  7  9    8  5  

0  3  1  1    7  9  null  8  5  

0  3  1  1  4  7  9  null  8  5  

0  3  1  1  4  null    7  8  5  

右指针指向9，9>flag，继续左移，然后红绿指针相遇，结束

我们把flag放入null，即形成了新的序列

0  3  1  1  4  4  9  7  8  5

我们把左侧序列0  3  1  1  4

和右侧序列9  7  8  5

分别如上做，即可得到有序序列

C++模板代码：

template<typename value_type, typename value_Ptr>
void quick_sort(value_Ptr begin, value_Ptr end)          //逾尾
{
    if (begin == end)return;

    value_type flag = *begin;

    value_Ptr l = begin, r = end;
    r--;
    while (l < r)
    {
        while (l < r && *r > flag)r--;
        if (l < r)*(l++) = *r;
        while (l < r && *l < flag)l++;
        if (l < r)*(r--) = *l;
    }
    *l = flag;
    quick_sort<value_type>(begin, l);
    quick_sort<value_type>(l + , end);
}

测试以及使用

#include <iostream>
#include <vector>
using namespace std;

int main()
{
    ios::sync_with_stdio(false);

    int list[]{ ,,,,,,,,, };
    vector<int> v{ list,list +  };

    quick_sort<int>(list + , list + );
    quick_sort<int>(v.begin(), v.end());
    for (auto it : v)cout << it << " ";
    cout << endl;
    for (auto it : list)cout << it << " ";
    cout << endl;

    char list_[]{ 'r','c','','A','z','b','','','r', '' };
    vector<char>v_{ list_,list_ +  };

    quick_sort<char>(list_ + , list_ + );
    quick_sort<char>(v_.begin(), v_.end());
    for (auto it : v_)cout << it << " ";
    cout << endl;
    for (auto it : list_)cout << it << " ";
    cout << endl;
}

测试结果

效率为O(N * logN)

如果序列中有很多重复的元素，那么，那一长串的重复值就相当于一个非递减序列，按理说是不需要排序的，但是上述无法识别此情况，它依旧会把这一长串不必处理的序列进行处理，无疑将函数执行效率大打折扣

这时，我们就需要引入三路快排

二、三路快排

基本思路

给你一个序列，我们选择一个基数作为标准，小于基数的元素放于左侧区间，等于基数的元素放于中间区间，大于基数的元素放于右侧区间

整理好之后，我们将左侧区间和右侧区间如上做。

过程描述

我们用四指针扫描

l  r  用于扫描待处理的序列

equ_l   equ_r  用于记录两侧相等的区间

equ_l  = l = begin

r 和equ_r指向右侧

让l r向中间遍历，遇到不等于的情况和快排一样，留一个空位，依次填补即可，遇到相等的情况，左指针指向的值等于基数，那么就放于equ_l处，且equ_l++，右边同理

当l  r  相遇时，我们让四指针分别向两端移动，equ_l 所指的元素依次和 l 所指的元素交换，右侧同理，即可得到我们想要的序列，即  <  =  >

之后，我们将<区间和>区间分别如上做，即可得到有序序列

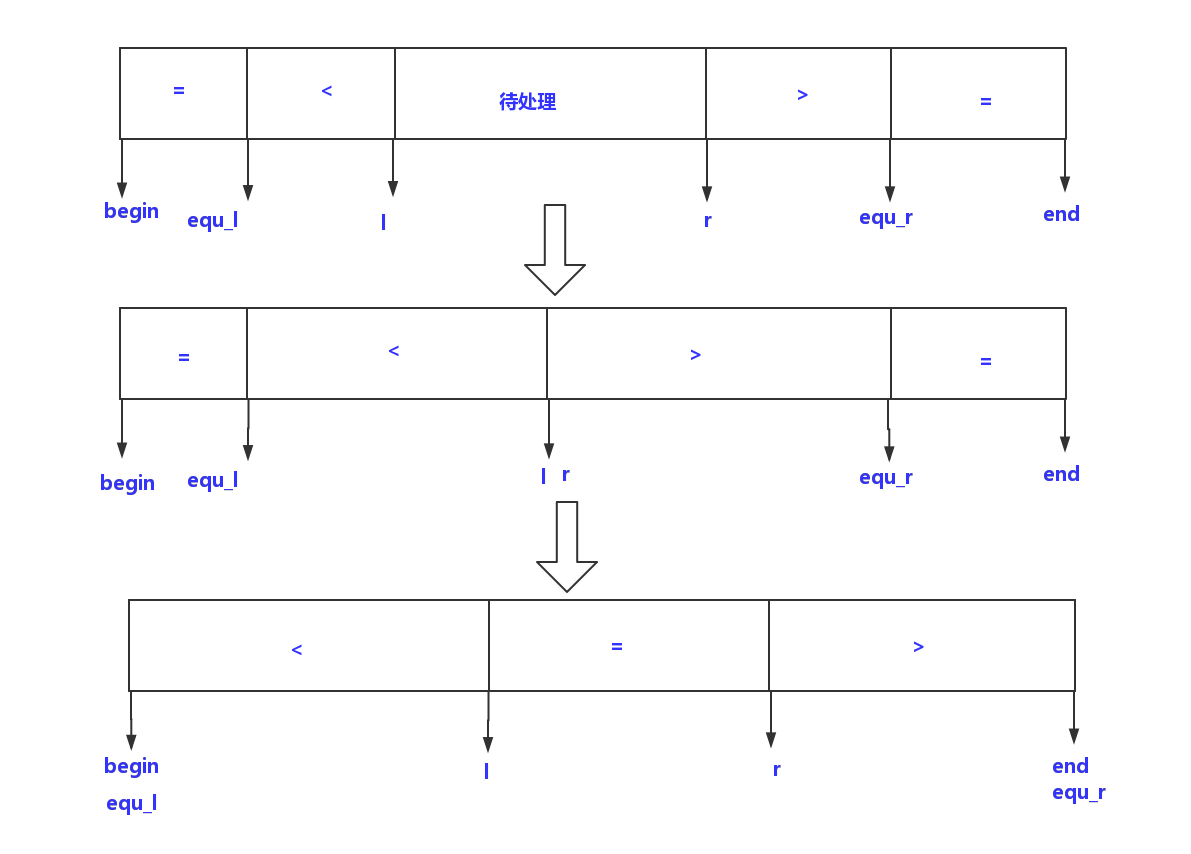
泛型模板代码：

template<typename value_type, typename value_Ptr>
void Tri_quick(const value_Ptr& begin, const value_Ptr& end)
{
    static auto swap = [](value_type& l, value_type& r)
    {
        if (l == r)return;
        value_type t{ l };
        l = r;
        r = t;
    };
    value_Ptr equ_l = begin, equ_r = end, l = begin, r = end;
    if (begin >= end || begin >= end - )return;       

  //上式：如果第二个条件成立的话，表达式1中的 ++l 就会解析 end 迭代器
    value_type flag = *l;
    while (l < r)
    {
        while (l < r && *(++l) < flag)if (l == end - )break;    //  表达式1
        while (l < r && flag < *(--r));
        if (*l != *r)    swap(*l, *r);
        if (*l == flag)    swap(*(++equ_l), *l);
        if (*r == flag)    swap(*(--equ_r), *r);
    }
    if (*l > flag)l--;    
 //此时l==r，可能l的值大于flag，我们不换，但是前面的一定小于等于flag，所以我们--
    while (equ_l > begin)swap(*(equ_l--), *(l--));
 //选择大于是因为equ_l如果为容器的begin迭代器，那么不允许--操作
    swap(*equ_l, *l);                                          
 //所以begin迭代器另做处理
    while (equ_r < end)swap(*(equ_r++), *(r++));
    Tri_quick<value_type>(begin, l);
    Tri_quick<value_type>(r, end);
}

测试及使用

#include <iostream>
#include <vector>
using namespace std;

int main()
{
    ios::sync_with_stdio(false);
    int list[]{ ,,,,,,,,, };
    vector<int> v{ list,list +  };
    Tri_quick<int>(list + , list + );
    for (auto it : list)cout << it << " ";
    cout << endl;
    Tri_quick<int>(v.begin(), v.end());
    for (auto it : v)cout << it << " ";
    cout << endl;

    char list_[]{ 'r','c','','A','z','b','','','r', '' };
    vector<char>v_{ list_,list_ +  };

    Tri_quick<char>(list_ + , list_ + );
    Tri_quick<char>(v_.begin(), v_.end());
    for (auto it : v_)cout << it << " ";
    cout << endl;
    for (auto it : list_)cout << it << " ";
    cout << endl;
}

注：三路快排中即使没有重复元素，那也最差退化到二路快排的效率，效率不会低于二路快排

这就是今天的多路快排，关于快排有很多不适应的情况，也有很多优化的算法，关于其他的算法，大家可以去其他地方学习，这里不做赘述

如果有什么问题，请于下方评论区留言。

感谢您的阅读，生活愉快~