转载：GBDT算法梳理

学习内容：

前向分布算法

负梯度拟合

损失函数

回归

二分类，多分类

正则化

优缺点

sklearn参数

应用场景

转自：https://zhuanlan.zhihu.com/p/58105824

GBDT是一种采用加法模型（即基函数的线性组合）与前向分步算法并以决策树作为基函数的提升方法。通俗来说就是，该算法由多棵决策树组成，所有树的结论加起来形成最终答案。

一、前向分步算法（考虑加法模型）

要理解GBDT算法，得先来了解一下什么是前向分步算法。下面一起来瞧瞧。

加法模型是这样的：

$f(x)=\sum_{m=1}^{M}{\beta_{m}b(x;\gamma_{m})}$ （就是基学习器的一种线性组合啦）

其中， $b(x;\gamma_{m})$ 为基函数， $\gamma_{m}$ 为基函数的参数， $\beta_{m}$ 为基函数的系数。

在给定训练数据及损失函数 $L（y,f(x)）$ 的条件下，学习加法模型成为损失函数极小化问题：

$min_{\beta_{m},\gamma_{m}}\sum_{i=1}^{N}{L(y_{i},\sum_{m=1}^{M}{\beta_{m}b(x_{i};\gamma_{m})})}$ （同时求解那么多参数，好复杂）

前向分步算法求解这一优化问题的思路：因为学习的是加法模型，如果能够从前向后，每一步只学习一个基函数及其系数，逐步去逼近上述的目标函数式，就可简化优化的复杂度，每一步只需优化如下损失函数：

$min_{\beta,\gamma}\sum_{i=1}^{N}{L(y_{i},\beta}b(x;\gamma))$ （每步学习一个基函数和系数）

前向分步算法流程：

--------------------------------------------------------------------------------------------

输入：训练数据集T=({ $(x_{1},y_{1}),(x_{2},y_{2}),...(x_{N},y_{N})$ })；损失函数L(y,f(x))；基函数集{ $b(x;\gamma)$ }；

输出：加法模型f(x)

(1) 初始化 $f_{0}(x)=0$

(2) 对m=1,2,...,M

(a) 极小化损失函数

$（\beta_{m},\gamma_{m}）=arg min_{\beta,\gamma}\sum_{i=1}^{N}{L(y_{i},f_{m-1}(x_{i})+\beta}b(x_{i};\gamma))$

得到参数 $\beta_{m},\gamma_{m}$

(b)更新

$f_{m}(x)=f_{m-1}(x)+\beta_{m}b(x;\gamma_{m})$

(3)得到加法模型

$f(x)=f_{M}(x)=\sum_{m=1}^{M}{\beta_{m}}b(x;\beta_{m})$

------------------------------------------------------------------------------------------

可见，前向分步算法将同时求解从m=1到M所有参数 $\beta_{m},\gamma_{m}$ 的优化问题简化成逐步求解各个 $\beta_{m},\gamma_{m}$ 的优化问题了。

二、负梯度拟合

1.提升树算法

了解完前向分步算法，再来看看什么是提升树算法。

提升方法实际采用加法模型与前向分步算法，以决策树作为基函数的提升方法称为提升树。注意，这里的决策树为CART回归树，不是分类树。当问题是分类问题时，采用的决策树模型为分类回归树。为什么要采用决策树作为基函数呢？它有以下优缺点：

优点

可解释性强
可处理混合类型特征
具有伸缩不变性（不用归一化特征）
有特征组合的作用
可自然处理缺失值
对异常点鲁棒
有特征选择作用
可扩展性强，容易并行

缺点

缺乏平滑性（回归预测时输出值只能是输出有限的若干种数值）
不适合处理高维稀疏数据

由于树的线性组合可以很好地拟合训练数据，即使数据中的输入与输出之间的关系很复杂也是如此。

提升树模型可表示为：

$f_{M}(x)=\sum_{m=1}^{M}{T(x;\theta_{m})}$

其中， $T(x;\theta_{m})$ 表示决策树; $\theta_{m}$ 为决策树的参数;M为树的个数;M为树的个数。

针对不同的问题，提升树算法的形式有所不同，其主要区别在于使用的损失函数不同。而损失函数的不同，决策树要拟合的值也会不同。就一般而言，对于回归问题的提升树算法来说，若损失函数是平方损失函数，每一步只需简单拟合当前模型的残差。

下面看一下在回归问题下，损失函数为平方损失函数的算法流程：

--------------------------------------------------------------------------------------------

输入：训练数据集T={ $(x_{1},y_{1}),(x_{2},y_{2}),...,(x_{N},y_{N})$ }， $x_{i}\in\chi\subseteq R^{n},y_{i}\in\gamma\subseteq R$ ；

输出：提升树 $f_{M}(x)$

(1)初始化 $f_{0}(x)=0$

(2)对m=1,2,...,M

(a)计算残差

$r_{mi}=y_{i}-f_{m-1}(x_{i}),i=1,2,...N$

(b)拟合残差 $r_{mi}$ 学习一个回归树，得到 $T(x;\theta_{m})$

(c)更新 $f_{m}(x)=f_{m-1}(x)+T(x;\theta_{m})$

(3)得到回归问题提升树

$f_{M}(x)=\sum_{m=1}^{M}{T(x;\theta_{m})}$

--------------------------------------------------------------------------------------------

2.梯度提升

提升树用加法模型与前向分布算法实现学习的优化过程。当损失函数为平方损失和指数损失函数时，每一步优化是很简单的。但对于一般损失函数而言，往往每一步都不那么容易。对于这问题，Freidman提出了梯度提升算法。这是利用最速下降法的近似方法，其关键是利用损失函数的负梯度在当前模型的值：

$-[\frac{\partial L(y,f(x_{i}))}{\partial f(x_{i})}]_{f(x)=f_{m-1}(x)}$

作为回归问题在当前模型的残差的近似值，拟合一个回归树。

为什么要拟合负梯度呢？这就涉及到泰勒公式和梯度下降法了。

泰勒公式的形式是这样的：

定义：泰勒公式是一个用函数在某点的信息描述其附近取值的公式。
基本形式： $f(x)=\sum_{n=0}^{\infty}{\frac{f^{(n)}(x_{0})}{n!}}(x-x_{0})^{n}$
一阶泰勒展开： $f(x)\approx f(x_{0})+f^{'}(x_{0})(x-x_{0})$

梯度下降法

在机器学习任务中，需要最小化损失函数 $L(\theta)$ ，其中 $\theta$ 是要求解的模型参数。梯度下降法常用来求解这种无约束最优化问题，它是一种迭代方法：选择初值 $\theta^{0}$ ，不断迭代更新 $\theta$ 的值，进行损失函数极小化。

迭代公式： $\theta^{t}=\theta^{t-1}+\Delta\theta$
将 $L(\theta^{t})$ 在 $\theta^{t-1}$ 处进行一阶泰勒展开： $L(\theta^{t})=L(\theta^{t-1}+\Delta\theta)\approx L(\theta^{t-1})+L^{'}(\theta^{t-1})\Delta\theta$
要使得 $L(\theta^{t})<L(\theta^{t-1})$ ，可取： $\Delta\theta=-\alpha L^{'}(\theta^{t-1})$ ，则： $\theta^{t}=\theta^{t-1}-\alpha L^{'}(\theta^{t-1})$ ，这里 $\alpha$ 是步长，一般直接赋值一个小的数。

相对的，在函数空间里，有 $f^{t}(x)=f^{t-1}(x)+f_{t}(x)$

此处把 $L(f^{t}(x))$ 看成提升树算法的第t步损失函数的值， $L(f^{t-1}(x))$ 为第t-1步损失函数值，要使 $L(f^{t}(x))<L(f^{t-1}(x))$ ，则需要 $f_{t}(x)=-\alpha g_{t}(x)$ ，此处 $-g_{t}(x)$ 为当前模型的负梯度值，即第t步的回归树需要拟合的值。

至于GBDT的具体算法流程，在后续回归与分类问题会分开说明。

三、损失函数

在GBDT算法中，损失函数的选择十分重要。针对不同的问题，损失函数有不同的选择。

1.对于分类算法，其损失函数一般由对数损失函数和指数损失函数两种。

(1)指数损失函数表达式：

$L(y,f(x))=e^{(-yf(x))}$

(2)对数损失函数可分为二分类和多分类两种。

2.对于回归算法，常用损失函数有如下4种。

(1)平方损失函数：

$L(y,f(x))=(y-f(x))^{2}$

(2)绝对损失函数：

$L(y,f(x)）=|y-f(x)|$

对应负梯度误差为：

$sign(y_{i}-f(x_{i}))$

(3)Huber损失，它是均方差和绝对损失的折中产物，对于远离中心的异常点，采用绝对损失误差，而对于靠近中心的点则采用平方损失。这个界限一般用分位数点度量。损失函数如下

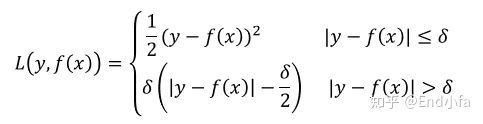
对应的负梯度误差为：

（4）分位数损失。它对应的是分位数回归的损失函数，表达式为：

$L(y,f(x))=\sum_{y\geq f(x)}^{}{\theta|y-f(x)|}+\sum_{y<f(x)}^{}{(1-\theta)|y-f(x)|}$

其中 $\theta$ 为分位数，需要我们在回归之前指定。对应的负梯度误差为：

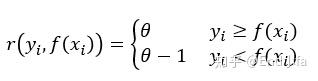
对于Huber损失和分位数损失，主要用于健壮回归，也就是减少异常点对损失函数的影响。

四、回归问题

梯度提升算法（回归问题）流程：

--------------------------------------------------------------------------------------------

输入：训练数据集T={ $(x_{1},y_{1}),(x_{2},y_{2}),...,(x_{N},y_{N})$ }， $x_{i}\in\chi\subseteq R^{n},y_{i}\in\gamma\subseteq R$ ；损失函数L(y,f(x))；

输出：回归树 $\tilde{f}(x)$

(1)初始化

$f_{0}=arg min_{c}\sum_{i=1}^{N}{L(y_{i},c})$ 注：估计使损失函数极小化的常数值，它是只有一个根结点的树

(2)对m=1,2,...,M

(a)对i=1,2,...N，计算

$r_{mi}=-[\frac{\partial L(y_{i},f(x_{i}))}{\partial f(x_{i})}]_{f(x)=f_{m-1}(x)}$ 注：计算损失函数在当前模型的值，作为残差的估计

(b)对 $r_{mi}$ 拟合一个回归树，得到第m棵树的叶结点区域 $R_{mj}$ ,j=1,2,...,J

(c)对j=1,2,...,J，计算

$c_{mj}=arg min_{c}\sum_{x_{j}\in R_{mj}}^{}{L(y_{i},f_{m-1}(x_{i})+c)}$ 注：在损失函数极小化条件下，估计出相应叶结点区域的值

(d)更新

$f_{m}(x)=f_{m-1}(x)+\sum_{j=1}^{J}{c_{mj}I(x\in R_{mj})}$

(3)得到回归树

$\tilde{f}(x)=f_{M}(x)=\sum_{m=1}^{M}{}\sum_{j=1}^{J}{c_{mj}I(x\in R_{mj})}$

--------------------------------------------------------------------------------------------

五、分类问题（二分类与多分类）

这里看看GBDT分类算法，GBDT的分类算法从思想上和GBDT的回归算法没有区别，但是由于样本输出不是连续的值，而是离散的类别，导致我们无法直接从输出类别去拟合输出类别的误差。

为了解决这个问题，主要有两个方法，一个是用指数损失函数，此时GBDT退化为Adaboost算法。另一种方法用类似逻辑回归的对数似然函数的方法。也就是说，我们用的是类别的预测概率值和真实概率值的差来拟合损失。此处仅讨论用对数似然函数的GBDT分类。对于对数似然损失函数，我们有又有二元分类和的多元分类的区别。

1.二分类GBDT算法

　　对于二分类GBDT，如果用类似逻辑回归的对数似然损失函数，则损失函数为：

　　 $L(y,f(x))=log(1+exp(-yf(x)))$

　　其中 $y\in$ {-1,1}。此时的负梯度误差为：

　　 $r_{ti}=-[\frac{\partial L(y,f(x_{i}))}{\partial f(x_{i})}_{f(x)=f_{t-1}(x)}=\frac{y_{i}}{1+exp(y_{i}f(x_{i}))}$

　　对于生成的决策树，我们各个叶子节点的最佳负梯度拟合值为

　　 $c_{tj}=arg min_{c}\sum_{x_{i}\in R_{tj}}^{}{log(1+exp(-y_{i}(f_{t-1}(x_{i})+c})))$

　　由于上式比较难优化，我们一般使用近似值代替

　　 $c_{tj}=\frac{\sum_{x_{i}\in R_{tj}}^{}{r_{tj}}}{\sum_{x_{i}\in R_{tj}}^{}{|r_{tj}|(1-|r_{tj}|)}}$

　　除了负梯度计算和叶子节点的最佳负梯度拟合的线性搜索，二分类GBDT与GBDT回归算法过程相同。

2.多分类GBDT算法

　　多分类GBDT比二分类GBDT复杂些，对应的是多元逻辑回归和二元逻辑回归的复杂度差别。假设类别数为K，则此时我们的对数似然损失函数为：

　　 $L(y,f(x))=-\sum_{k=1}^{K}{y_{k}log(p_{k}(x))}$

　　其中如果样本输出类别为k，则 $y_{k}$ =1.第k类的概率 $p_{k}(x)$ 的表达式为：

　　 $p_{k}(x)=\frac{exp(f_{k}(x))}{\sum_{l=1}^{K}{exp(f_{l}(x))}}$

　　集合上两式，我们可以计算出第t轮的第i个样本对应类别l的负梯度误差为：

　　 $t_{til}=-[\frac{\partial L(y_{i},f(x_{i}))}{\partial f(x_{i})}]_{f_{k}(x)=f_{l,t-1}(x)}=y_{il}-p_{l,t-1}(x_{i})$

　　观察上式可以看出，其实这里的误差就是样本i对应类别l的真实概率和t-1轮预测概率的差值。

　　对于生成的决策树，我们各个叶子节点的最佳负梯度拟合值为：

　　 $c_{tjl}=arg min_{c_{jl}}\sum_{i=0}^{m}{}\sum_{k=1}^{K}{L(y_{k},f_{t-1,l}(x)+\sum_{j=0}^{J}{c_{jl}I(x_{i}\in R_{tj})}})$

　　由于上式比较难优化，我们一般使用近似值代替

　　 $c_{tjl}=\frac{K-1}{K}\frac{\sum_{x_{i}\in R_{tjl}}^{}{r_{til}}}{\sum_{x_{i}\in R_{til}}^{}{|r_{til}|(1-|r_{til}|)}}$

　　除了负梯度计算和叶子节点的最佳负梯度拟合的线性搜索，多分类GBDT与二分类GBDT以及GBDT回归算法过程相同。

六、正则化

对GBDT进行正则化来防止过拟合，主要有三种形式。

　　　　1.给每棵数的输出结果乘上一个步长a（learning rate）。

　　　　　　对于前面的弱学习器的迭代：

　　　　　　 $f_{m}(x)=f_{m-1}(x)+T(x;\gamma_{m})$

　　　　　　加上正则化项，则有

　　　　　　 $f_{m}(x)=f_{m-1}(x)+aT(x;\gamma_{m})$

　　　　　　此处，a的取值范围为(0,1]。对于同样的训练集学习效果，较小的a意味着需要更多的弱学习器的迭代次数。通常我们用步长和迭代最大次数一起决定算法的拟合效果。

　　　　2.第二种正则化的方式就是通过子采样比例(subsample)。取值范围为(0,1]。

　　　　　　GBDT这里的做法是在每一轮建树时，样本是从原始训练集中采用无放回随机抽样的方式产生，与随机森立的有放回抽样产生采样集的方式不同。若取值为1，则采用全部样本进行训练，若取值小于1，则不选取全部样本进行训练。选择小于1的比例可以减少方差，防止过拟合，但可能会增加样本拟合的偏差。取值要适中，推荐[0.5,0.8]。

　　　　3.第三种是对弱学习器即CART回归树进行正则化剪枝。（如控制树的最大深度、节点的最少样本数、最大叶子节点数、节点分支的最小样本数等）

七、GBDT优缺点

1.GBDT优点

可以灵活处理各种类型的数据，包括连续值和离散值。
在相对较少的调参时间情况下，预测的准确率也比较高，相对SVM而言。
在使用一些健壮的损失函数，对异常值得鲁棒性非常强。比如Huber损失函数和Quantile损失函数。

2.GBDT缺点

由于弱学习器之间存在较强依赖关系，难以并行训练。可以通过自采样的SGBT来达到部分并行。

八、sklearn参数

在scikit-learning中，GradientBoostingClassifier对应GBDT的分类算法，GradientBoostingRegressor对应GBDT的回归算法。

具体算法参数情况如下：

GradientBoostingRegressor(loss=’ls’, learning_rate=0.1, n_estimators=100,

                subsample=1.0, criterion=’friedman_mse’, min_samples_split=2,

                min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_depth=3,

                min_impurity_decrease=0.0, min_impurity_split=None, init=None,

                random_state=None, max_features=None, alpha=0.9, verbose=0,

                max_leaf_nodes=None, warm_start=False, presort=’auto’,

                validation_fraction=0.1, n_iter_no_change=None, tol=0.0001)

参数说明：

n_estimators：弱学习器的最大迭代次数，也就是最大弱学习器的个数。
learning_rate：步长，即每个学习器的权重缩减系数a，属于GBDT正则化方化手段之一。
subsample：子采样，取值(0,1]。决定是否对原始数据集进行采样以及采样的比例，也是GBDT正则化手段之一。
init：我们初始化的时候的弱学习器。若不设置，则使用默认的。
loss：损失函数，可选{'ls'-平方损失函数，'lad'绝对损失函数-,'huber'-huber损失函数,'quantile'-分位数损失函数}，默认'ls'。
alpha：当我们在使用Huber损失"Huber"和分位数损失"quantile"时，需要指定相应的值。默认是0.9，若噪声点比较多，可适当降低这个分位数值。
criterion：决策树节搜索最优分割点的准则，默认是"friedman_mse"，可选"mse"-均方误差与'mae"-绝对误差。
max_features：划分时考虑的最大特征数，就是特征抽样的意思，默认考虑全部特征。
max_depth：树的最大深度。
min_samples_split：内部节点再划分所需最小样本数。
min_samples_leaf：叶子节点最少样本数。
max_leaf_nodes：最大叶子节点数。
min_impurity_split：节点划分最小不纯度。
presort：是否预先对数据进行排序以加快最优分割点搜索的速度。默认是预先排序，若是稀疏数据，则不会预先排序，另外，稀疏数据不能设置为True。
validationfraction：为提前停止而预留的验证数据比例。当n_iter_no_change设置时才能用。
n_iter_no_change：当验证分数没有提高时，用于决定是否使用早期停止来终止训练。

八、GBDT应用场景

GBDT几乎可以用于所有回归问题（线性/非线性），相对loigstic regression仅能用于线性回归，GBDT的适用面非常广。亦可用于分类问题。