深度研究：回归模型评价指标R2_score

回归模型的性能的评价指标主要有：RMSE(平方根误差)、MAE（平均绝对误差）、MSE(平均平方误差)、R2_score。但是当量纲不同时，RMSE、MAE、MSE难以衡量模型效果好坏。这就需要用到R2_score，实际使用时，会遇到许多问题，今天我们深度研究一下。

预备知识

搞清楚R2_score计算之前，我们还需要了解几个统计学概念。

若用$y_i$表示真实的观测值，用$\bar{y}$表示真实观测值的平均值，用$\hat{y_i}$表示预测值,则：

回归平方和：SSR

$$SSR = \sum_{i=1}^{n}(\hat{y_i} - \bar{y})^2$$

即估计值与平均值的误差，反映自变量与因变量之间的相关程度的偏差平方和

残差平方和：SSE

$$SSE = \sum_{i=1}^{n}(y_i-\hat{y_i} )^2$$

即估计值与真实值的误差，反映模型拟合程度

总离差平方和：SST

$$SST =SSR + SSE= \sum_{i=1}^{n}(y_i - \bar{y})^2$$

即平均值与真实值的误差，反映与数学期望的偏离程度

R2_score计算公式

R^2 score，即决定系数，反映因变量的全部变异能通过回归关系被自变量解释的比例。计算公式：

$$R^2=1-\frac{SSE}{SST}$$

即

$$R^2 = 1 - \frac{\sum_{i=1}^{n} (y_i - \hat{y}_i)^{2}{\sum_{i=1}}{n} (y_i - \bar{y})^2}$$

进一步化简

$$R^2 = 1 - \frac{\sum\limits_i(y_i - y_i)^2 / n}{\sum\limits_i(y_i - \hat{y})^2 / n} = 1 - \frac{RMSE}{Var}$$

分子就变成了常用的评价指标均方误差MSE，分母就变成了方差。

对于$R^2$可以通俗地理解为使用均值作为误差基准，看预测误差是否大于或者小于均值基准误差。

R2_score = 1，样本中预测值和真实值完全相等，没有任何误差，表示回归分析中自变量对因变量的解释越好。

R2_score = 0。此时分子等于分母，样本的每项预测值都等于均值。

R2_score不是r的平方，也可能为负数(分子>分母)，模型等于盲猜，还不如直接计算目标变量的平均值。

r2_score使用方法

根据公式，我们可以写出r2_score实现代码

1- mean_squared_error(y_test,y_preditc)/ np.var(y_test)

也可以直接调用sklearn.metrics中的r2_score

sklearn.metrics.r2_score(y_true, y_pred, sample_weight=None, multioutput='uniform_average')
#y_true：观测值
#y_pred：预测值
#sample_weight：样本权重，默认None
#multioutput：多维输入输出，可选‘raw_values’, ‘uniform_average’, ‘variance_weighted’或None。默认为’uniform_average’;
raw_values：分别返回各维度得分
uniform_average：各输出维度得分的平均
variance_weighted：对所有输出的分数进行平均，并根据每个输出的方差进行加权。

sklearn.metrics.r2_score使用方法

import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import r2_score
#导入数据
diabetes_X, diabetes_y = datasets.load_diabetes(return_X_y=True)
diabetes_X = diabetes_X[:, np.newaxis, 2]
#划分测试集验证集
diabetes_X_train = diabetes_X[:-20]
diabetes_X_test = diabetes_X[-20:]
diabetes_y_train = diabetes_y[:-20]
diabetes_y_test = diabetes_y[-20:]
# 创建线性回归模型
regr = linear_model.LinearRegression()
# 训练模型
regr.fit(diabetes_X_train, diabetes_y_train)
# 预测
diabetes_y_pred = regr.predict(diabetes_X_test)
# 模型评价
print('r2_score: %.2f'
      % r2_score(diabetes_y_test, diabetes_y_pred))
# 绘制预测效果图
plt.scatter(diabetes_X_test, diabetes_y_test,  color='black')
plt.plot(diabetes_X_test, diabetes_y_pred, color='blue', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()

r2_score: 0.47

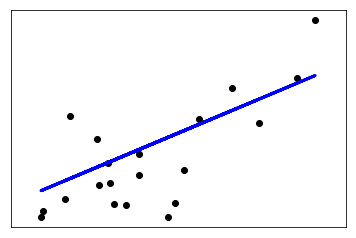
r2_score偏小，预测效果一般。

注意事项

1、$R^2$ 一般用在线性模型中（非线性模型也可以用）

2、$R^2$不能完全反映模型预测能力的高低,某个实际观测的自变量取值范围很窄，但此时所建模型的R2 很大，但这并不代表模型在外推应用时的效果肯定会很好。

3、数据集的样本越大，R²越大，因此，不同数据集的模型结果比较会有一定的误差，此时可以使用Adjusted R-Square (校正决定系数）,能对添加的非显著变量给出惩罚:

$$R^{2_{\text{Adj}}=1-(1-R}2)\frac{n-p-1}{n-1}$$

n是样本的个数，p是变量的个数

Reference

https://scikit-learn.org

https://zhuanlan.zhihu.com/p/36305931

https://www.jianshu.com/p/9ee85fdad150

https://blog.csdn.net/Dear_D/article/details/86144696

https://blog.csdn.net/shy19890510/article/details/79375062