题解和总结——noip2019集训测试赛（一）贪吃蛇+字符串+都城

Problem A: 贪吃蛇

描述



Input



Output



Sample Input

【样例输入1】

4 5

##...

..1#@

432#.

...#.

【样例输出1】

4

【样例输入2】

4 4

#78#

.612

.543

..@.

【样例输出2】

6

【样例输入3】

3 2

3@

2#

1#

【样例输出3】

-1

这道题就是一个简单的广搜，储存蛇头位置，步数和蛇的身体的各个部分的位置。注意，要关照一下蛇不能越过自己的身体。

代码：

#include<bits/stdc++.h>
using namespace std;
struct zuobiao
{
   int x,y;
}a[11];
struct data
{
   int x,y,sum;
   zuobiao number[10];
}b;
queue<data> q;
char ch;
int n,m,is[16][16],k,f[4][2]={{0,1},{1,0},{0,-1},{-1,0}};
bool vis[16][16],flag;
int main()
{
   scanf("%d%d",&n,&m);
   for(int i=1;i<=n;i++)
   {
   	for(int j=1;j<=m;j++)
   	{
   		cin>>ch;
   		if(ch=='#')
   		{
   			is[i][j]=10;
   		}else{
   			if(ch=='@')
   			{
   			    is[i][j]=11;
   			}else{
   				if(ch>='1'&&ch<='9')
   				{
   					k++;
   					b.number[ch-'0'].x=i;
   					b.number[ch-'0'].y=j;
   					if(ch=='1')
   					{
   						b.x=i;
   						b.y=j;
   						b.sum=0;
   					}
   				}
   			}
   		}
   	}
   }
   q.push(b);//放入队列
   while(!q.empty())
   {
   	data u=q.front();
   	data p=u;
   	q.pop();
   	for(int i=0;i<4;i++)
   	{
   		u=p;
   		int xx=u.number[1].x+f[i][0];
   		int yy=u.number[1].y+f[i][1];
   		int num=u.sum;
   		flag=0;
   		for(int i=1;i<k;i++)//可以咬尾巴，尾巴会走
   		{
   			if(xx==u.number[i].x&&yy==u.number[i].y)
   			{
   				flag=1;
   				break;
   			}
   		}
   		if(flag||is[xx][yy]==10||vis[xx][yy]||xx>n||xx<1||yy>m||yy<1)
   		{
   			continue;
   		}
   		if(is[xx][yy]==11)
   		{
   			printf("%d\n",num+1);
   			return 0;
   		}
   		for(int i=k;i>1;i--)//移动蛇身
   		{
   			u.number[i].x=u.number[i-1].x;
   			u.number[i].y=u.number[i-1].y;
   		}
   		u.sum++;
   		vis[u.number[1].x][u.number[1].y]=1;//更新
   		u.number[1].x=xx;
   		u.number[1].y=yy;
   		q.push(u);
   	}
   }
   puts("-1");//若无解
   return 0;
}

Problem B: 字符串

UPD:本题字符集为全体小写字母

描述：



Input



Output



Sample Input

5
1 abc
3 abcabc
0 abc
3 aba
1 abababc

Sample Output

2
2

这一题题目描述明确地提示了一件事——本题是字符串题，虽然说了是强制在线，可能有点假，因为我们可以优化修改和查询的时间复杂度从而不理会强制在线带来的难题。

我们提前建好AC自动机的fail树记录好每个字符串的起始点，长度，并把它们合并到一起。 在fail树上的_a[s]_ 的值用线段树或者树状数组维护，dfs遍历打上时间戳。改修改的修改，该查询的查询，最后可以得出答案（某巨佬的想法）。

然后我说说个人有几个疑惑的点，为什么是这样做：

1.为什么可以用线段树或树状数组维护？

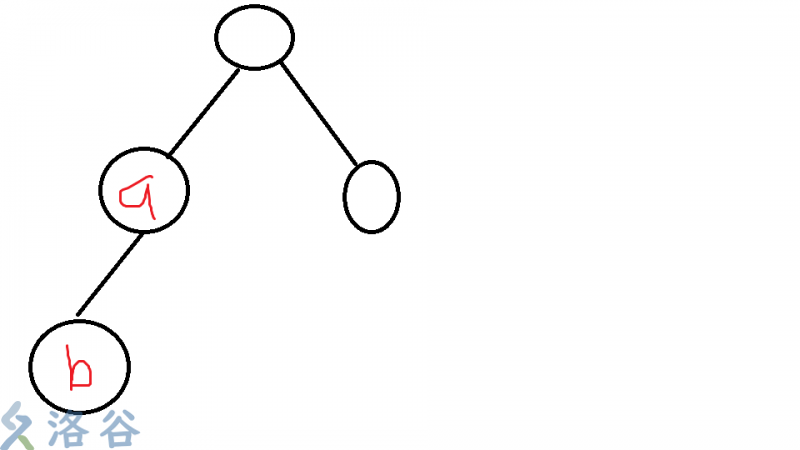
如图，点a的值加1，点b的值必定会加1。

2.这句话为什么？

add(dfn[num[i]]+size[num[i]],1);

很简单：



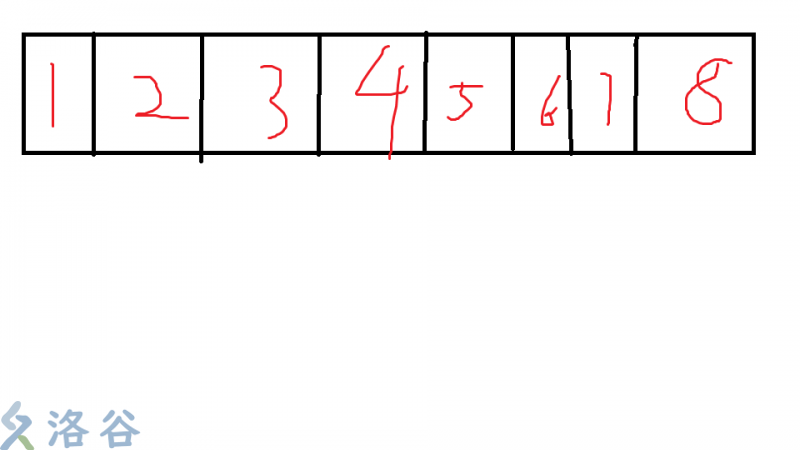
如果其中的4到6这个区间一起加了个1，在这个区间前和区间中的查找不会有什么影响，但区间后的一段就因为4到6加了个1，而被迫加了个1，所以我们在增加4到6区间时，也要相对应地在这个区间后减去1。

#include<bits/stdc++.h>
using namespace std;
int to[2000001],tot,nxt[2000001],head[2000001],len[2000001],cnt,num[2000001],dfn[2000001],indew,size[2000001],c[2000001],n,op[2000001],l,begi[2000001],mark;
char s[2000001],ch[2000001];
long long ans;
struct data
{
    int b[26],fail;
}a[2000001];
void adde(int u,int v)
{
    to[++tot]=v;
    nxt[tot]=head[u];
    head[u]=tot;
}
void build(char ch[],int id)
{
    int root=0;
    for(int i=0;i<len[id];i++)
    {
        int xx=ch[i]-'a';
        if(!a[root].b[xx])
        {
            a[root].b[xx]=++cnt;
        }
        root=a[root].b[xx];
    }
    num[id]=root;
}
void fail()//建fail树
{
    queue<int> q;
    for(int i=0;i<26;i++)
    {
        if(a[0].b[i])
        {
            a[a[0].b[i]].fail=0;
            q.push(a[0].b[i]);
        }
    }
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        for(int i=0;i<26;i++)
        {
            if(a[u].b[i])
            {
                a[a[u].b[i]].fail=a[a[u].fail].b[i];
                q.push(a[u].b[i]);
            }else{
                a[u].b[i]=a[a[u].fail].b[i];
            }
        }
    }
    for(int i=1;i<=cnt;i++)
    {
        adde(a[i].fail,i);
    }
}
void dfs(int u)
{
    dfn[u]=++indew;
    size[u]=1;
    for(int i=head[u];i;i=nxt[i])
    {
        int v=to[i];
        dfs(v);
        size[u]+=size[v];
    }
}
int lowbit(int x)
{
    return x&(-x);
}
void add(int x,int y)
{
    for(;x<=indew;x+=lowbit(x))
    {
        c[x]+=y;
    }
}
long long ask(int x)
{
    int ans1=0;
    for(;x;x-=lowbit(x))
    {
        ans1+=c[x];
    }
    return ans1;
}
void work(int l,int r)
{
    long long root=0;
    for(int i=l;i<=r;i++)
    {
        int xx=s[i]-'a';
        root=a[root].b[xx];
        ans+=ask(dfn[root]);
    }
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d%s",&op[i],ch);
        len[i]=strlen(ch);
        begi[i]=l+1;
        build(ch,i);
        for(int j=0;j<len[i];j++)
        {
            s[++l]=ch[j];
        }
    }
    fail();//建fail树
    dfs(0);
    for(int i=1;i<=n;i++)
    {
        op[i]^=mark;
        if(op[i]==1)//树状数组
        {
            add(dfn[num[i]],1);
            add(dfn[num[i]]+size[num[i]],-1);
        }else{
            if(op[i]==2)
            {
                add(dfn[num[i]],-1);
                add(dfn[num[i]]+size[num[i]],1);
            }else{
                ans=0;
                work(begi[i],begi[i]+len[i]-1);
                printf("%lld\n",ans);
                mark^=abs(ans);
            }
        }
    }
    return 0;
}

Problem C: 都城

题目描述：



Input



Output

看题好像很玄乎地样子，但是我们画出图来发现——以一个点为都城所形成的树上相邻两点的计划更改数相差1且若a为b的father：ans[b]=ans[a]+1,反之则亦然。

那我们可以根据这一点想到了树形DP，两遍dfs，第一遍确定以一个点为都城的ans值，第二遍通过上边这个式子推出所有点的ans。

#include<bits/stdc++.h>
using namespace std;
struct data
{
    int y,fa;//记录原计划是x通往y还是y通往x是高速公路
};
vector<data> a[100001];
int ans[100001],n,x,y;
void dfs(int u,int fa)
{
    for(int i=0;i<a[u].size();i++)
    {
        data v=a[u][i];
        if(v.y==fa)
        {
            continue;
        }
        if(!v.fa)//求ans[1]
        {
            ans[1]++;
        }
        dfs(v.y,u);
    }
}
void dfs1(int u,int fa)
{
    for(int i=0;i<a[u].size();i++)
    {
        data v=a[u][i];
        if(v.y==fa)
        {
            continue;
        }
        if(!v.fa)//计算
        {
            ans[v.y]=ans[u]-1;
        }else{
            ans[v.y]=ans[u]+1;
        }
        dfs1(v.y,u);
    }
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<n;i++)
    {
        scanf("%d%d",&x,&y);
        a[x].push_back((data){
            y,1
        });
        a[y].push_back((data){
            x,0
        });
    }
    dfs(1,-1);
    dfs1(1,-1);
    for(int i=1;i<=n;i++)
    {
        printf("%d\n",ans[i]);
    }
    return 0;
}

总结：

这次考的不太好，主要是第三题考场上没有注意到相邻两点的值相差1，只能打了一个暴搜。