【深度学习】Focal Loss 与 GHM——解决样本不平衡问题

Focal Loss 与 GHM

Focal Loss

Focal Loss 的提出主要是为了解决难易样本数量不平衡（注意：这有别于正负样本数量不均衡问题）问题。下面以目标检测应用场景来说明。

1. 一些 one-stage 的目标检测器通常会产生很多数量的 anchor box，但是只有极少数是正样本，导致正负样本数量不均衡。这里假设我们计算分类损失函数为交叉熵公式。

2. 由于在目标检测中，大量的候选目标都是易分样本，这些样本的损失很低，但是由于数量极不平衡，易分样本数量相对来说太多，最终主导了总的损失，但是模型也应该关注那些难分样本（难分样本又分为普通难分样本和特别难分样本，后面即将讲到的GHM就是为了解决特别难分样本的问题）。

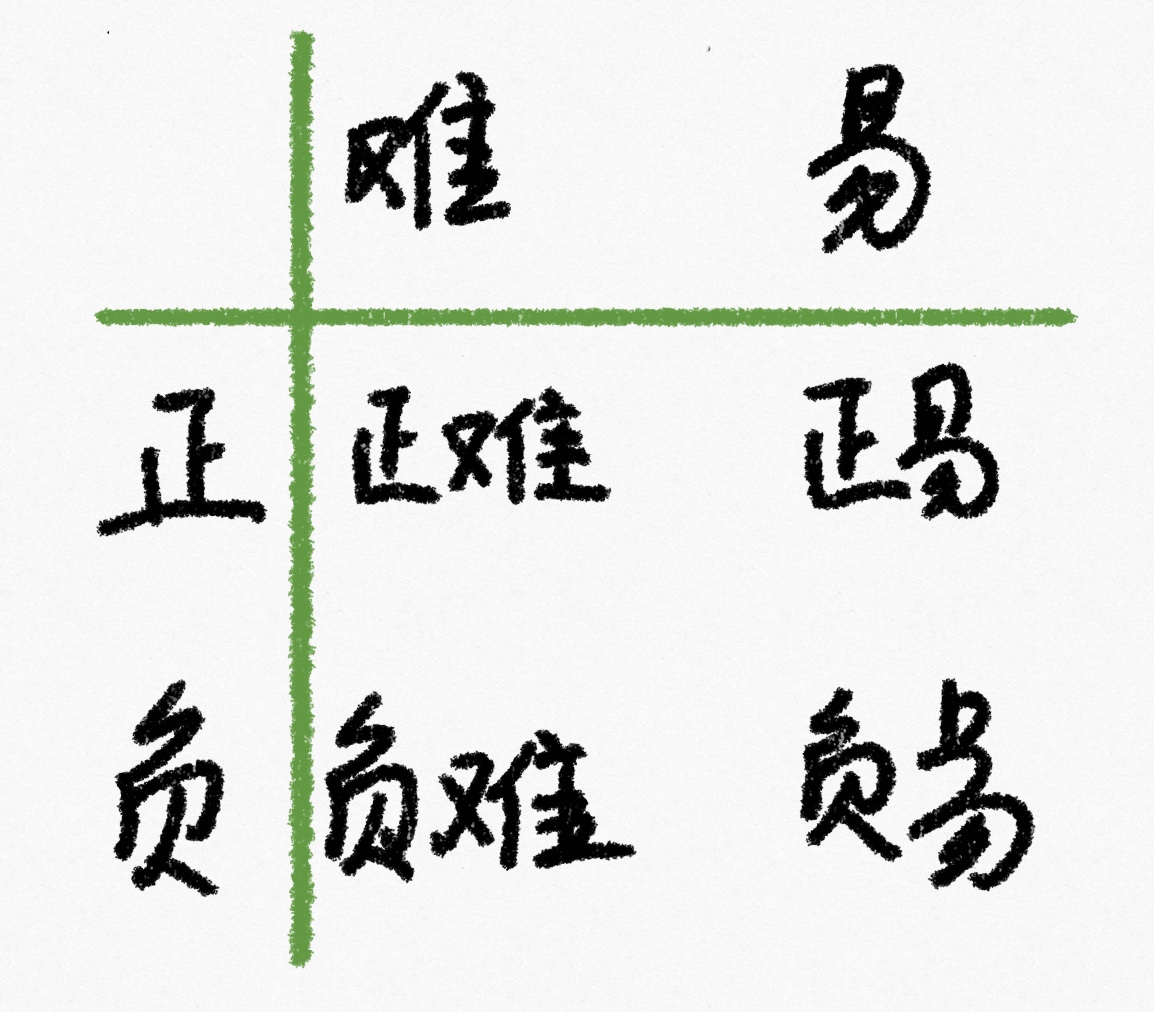
基于以上两个场景中的问题，Focal Loss 给出了很好的解决方法：

---

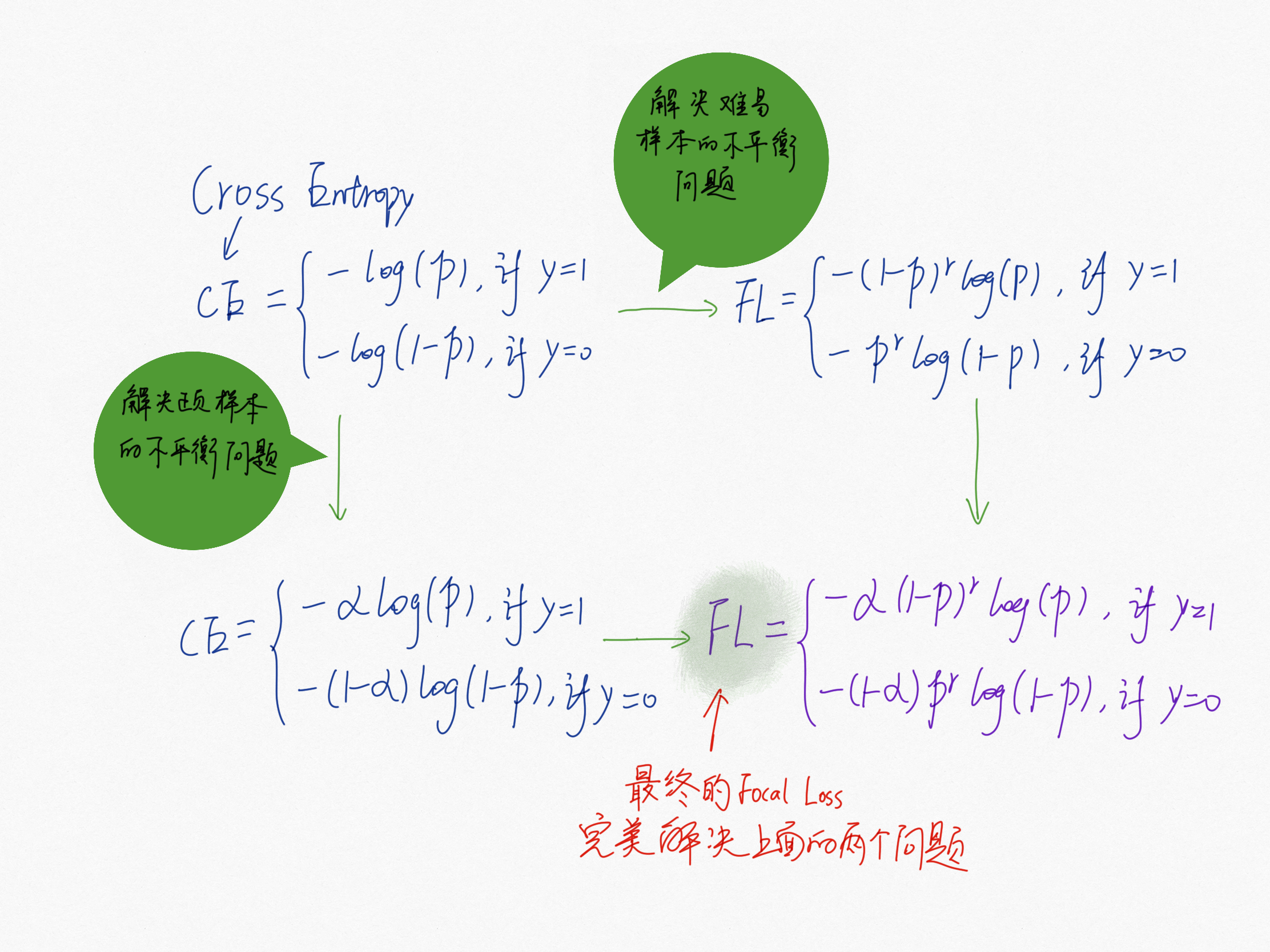
GHM

Focal Loss存在一些问题：

• 如果让模型过多关注 难分样本 会引发一些问题，比如样本中的离群点（outliers），已经收敛的模型可能会因为这些离群点还是被判别错误，总而言之，我们不应该过多关注易分样本，但也不应该过多关注难分样本；
• \(\alpha\) 与 \(\gamma\) 的取值全从实验得出，且两者要联合一起实验，因为它们的取值会相互影响。

几个概念：

1. 梯度模长g：\(g\) 正比于检测的难易程度，\(g\) 越大则检测难度越大，\(g\) 从交叉熵损失求梯度得来
   \[
   g=|p-p^*|=
   \begin{cases}
   1-p, & \text{if p* = 1} \\
   p, & \text{if p* = 0}
   \end{cases}
   \]
   \(p\) 是模型预测的概率，\(p^*\) 是 Ground-Truth 的标签（取值为1或者0）；

   \(g\) 正比于检测的难易程度，\(g\) 越大则检测难度越大；

2. 梯度模长与样本数量的关系：梯度模长接近于 0 时样本数量最多（这些可归类为易分样本），随着梯度模长的增长，样本数量迅速减少，但是当梯度模长接近于 1 时样本数量也挺多（这些可归类为难分样本）。如果过多关注难分样本，由于其梯度模长比一般样本大很多，可能会降低模型的准确度。因此，要同时抑制易分样本和难分样本！

   

3. 抑制方法之梯度密度 \(G(D)\)： 因为易分样本和特别难分样本数量都要比一般样本多一些，而我们要做的就是衰减 单位区间数量多的那类样本，也就是物理学上的密度概念。
   \[
   GD(g) = \frac{1}{l_{\epsilon}}\sum_{k=1}^{N}\delta_{\epsilon}(g_k, g)
   \]
   \(\delta_{\epsilon}(g_k, g)\) 表示样本 \(1 \sim N(样本数量)\) 中，梯度模长分布在 \((g-\frac{\epsilon}{2}, g+\frac{\epsilon}{2} )\) 范围内的样本个数，\(l_{\epsilon}(g)\) 代表了 \((g-\frac{\epsilon}{2}, g+\frac{\epsilon}{2} )\) 区间的长度；

4. 最后对每个样本，用交叉熵 \(CE\) \(\times\) 该样本梯度密度的倒数即可。

分类问题的GHM损失：
\[
L_{GHM-C} = \sum_{i=1}^{N}\frac{L_{CE}(p_i, p_i^*)}{GD(g_i)}
\]
回归问题的GHM损失：
\[
L_{GHM-R} = \sum_{i=1}^N \frac{ASL_1(d_i)}{GD(gr_i)}
\]
其中，\(ASL_1(d_i)\) 为修正的 smooth L1 Loss。

抑制效果：

---

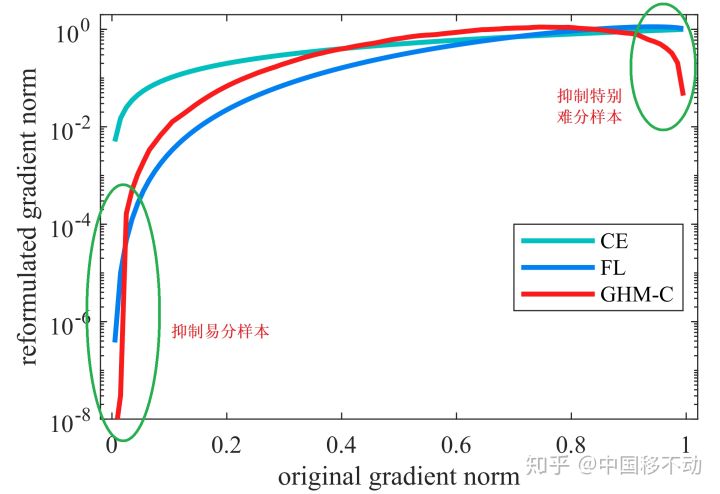
参考资料：

5分钟理解Focal Loss与GHM-解决样本不平衡利器——知乎