IEEE754 浮点数

1.阅读IEEE754浮点数

A,阶码是用移码表示的,这里会有一个127的偏移量,它的127相当于0,小于127时为负,大于127时为正,比如:10000001表示指数为129-127=2,表示真值为2^2,而01111110则表示2^(-1).
B, 尾数全都是小数点后面的数,
C, 但尾数中省略了一个1,因此尾数全为0时,也是1.0...00;
D,当尾数的值不为0时，尾数的最高有效位应为1，这称为浮点数的规格化表示

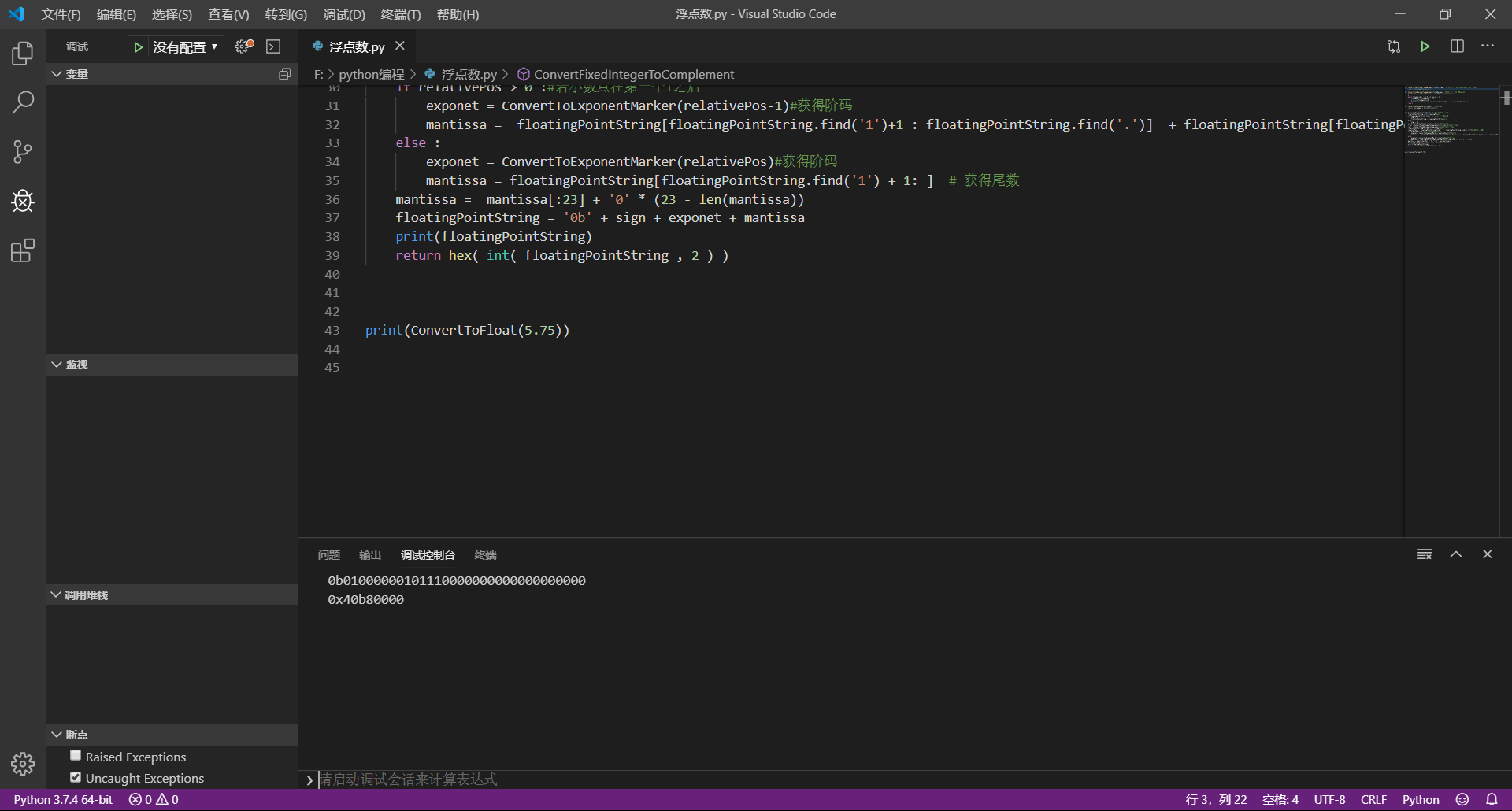
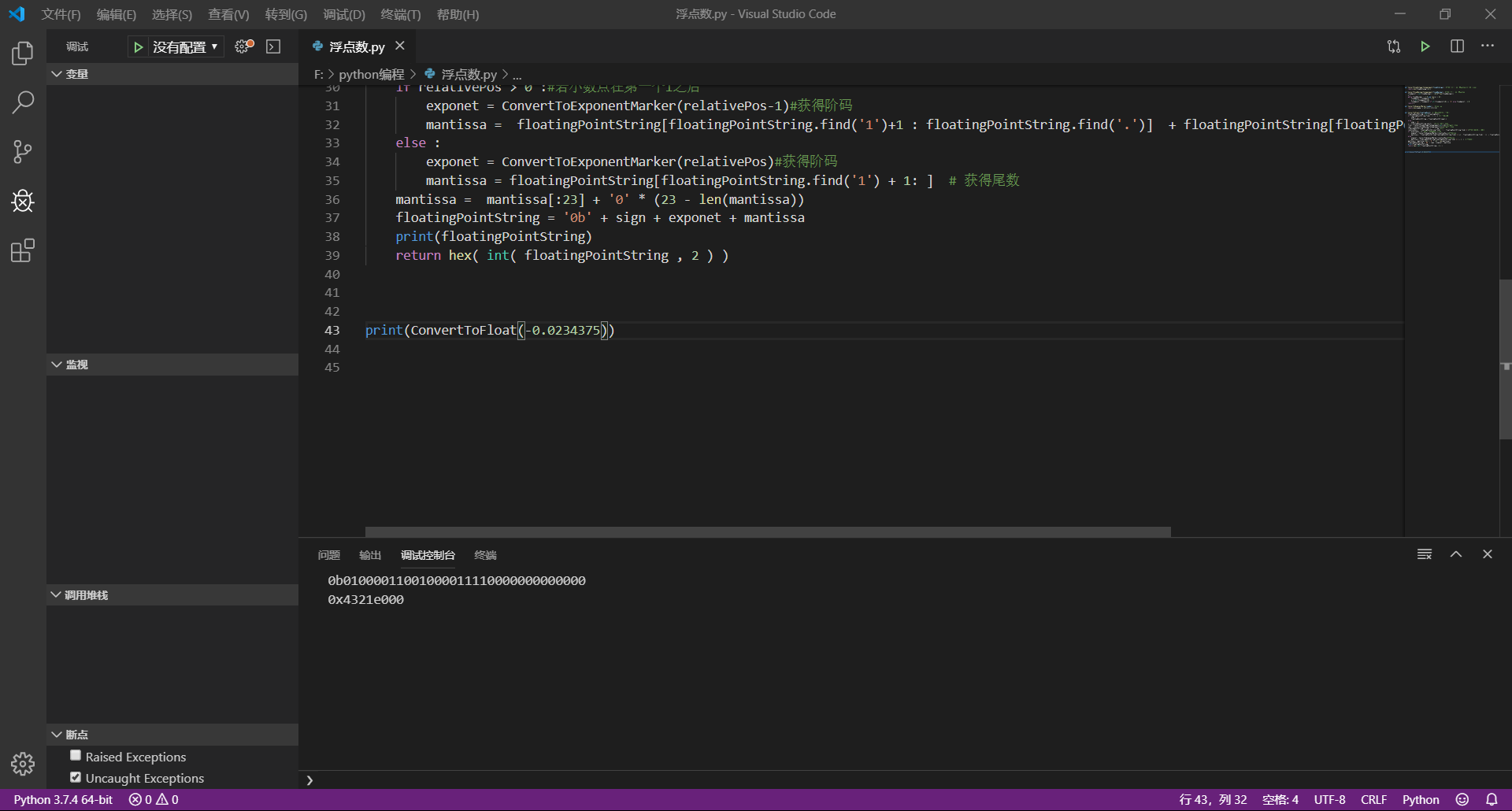
2.把十进制数5.75，161.875，-0.0234375 转化为单精度浮点数的二进制格式

自己转化的结果

01000000101110000000000000000000
01000011001000011110000000000000
10111100110000000000000000000000

浮点数转化工具的结果

使用python编程完成转化。

参考资料:

1.Python实现十进制小数转IEEE754单精度浮点数转换
2.python之def函数 - derezzed - 博客园
3.你必须理解的三大软件原则1_DRY

代码链接

浮点数转化

运行结果



IEEE754 浮点数的更多相关文章

  1. 震惊！计算机连0.3+0.6都算不对？浅谈IEEE754浮点数算数标准

    >>> 0.3+0.6 0.8999999999999999 >>> 1-0.9 0.09999999999999998 >>> 0.1+0.1+ ...

  2. 把一个IEEE754浮点数转换为IBM370浮点数的C#代码

    把一个IEEE754浮点数转换为IBM370浮点数的C#代码. 在这个网页上有古老的IBM370浮点格式的说明. // http://en.wikipedia.org/wiki/IBM_Floatin ...

  3. IEEE754浮点数

    前言 Go语言之父Rob Pike大神曾吐槽:不能掌握正则表达式或浮点数就不配当码农! You should not be permitted to write production code if ...

  4. IEEE754浮点数表示法

    IEEE二进制浮点数算术标准(ANSI/IEEE Std 754-1985)是一套规定如何用二进制表示浮点数的标准.就像"补码规则"建立了二进制位和正负数的一一对应关系一样,IEE ...

  5. IEEE Floating Point Standard (IEEE754浮点数表示法标准)

    浮点数与定点数表示法是我们在计算机中常用的表示方法 所以必须要弄懂原理,特别是在FPGA里面,由于FPGA不能像在MCU一样直接用乘除法. 定点数 首先说一下简单的定点数,定点数是克服整数表示法不能表 ...

  6. matlab中实现 IEEE754浮点数 与 一般十进制数之间 互相转换的方法

    ------------恢复内容开始------------ %2020/12/2 11:42:31clcformat long % IEEE754 to deca = '40800000'a = d ...

  7. IEEE754浮点数的转换

    将十进制数转换为单精度浮点数 如何将十进制数转换为单精度浮点数参考 首先要知道 IEEE浮点标准:V=(-1)^s * M * 2^E 1.符号(sign)s决定这个数是负数(s=1)还是正数,0(s ...

  8. IEEE754浮点数的表示方法

    https://blog.csdn.net/K346K346/article/details/50487127

  9. 作业：IEEE754浮点数

    人工转换: 5.75转换成二进制:101.11右移2位,补0:1.0111000000000000000000000000000000000000000000000000.10000000001 16 ...

随机推荐

  1. add to explorer context menu需不需要勾选

    添加到鼠标右键菜单,添加以后,可以直接右键文件,直接选择这个软件打开选择的文件,建议勾选

  2. linux系统安全加固

    版权声明:本文为博主原创文章,支持原创,转载请附上原文出处链接和本声明. 本文地址:https://www.cnblogs.com/wannengachao/p/12068256.html 1.文件上 ...

  3. TensorFlow从1到2（十三）图片风格迁移

    风格迁移 <从锅炉工到AI专家(8)>中我们介绍了一个"图片风格迁移"的例子.因为所引用的作品中使用了TensorFlow 1.x的代码,算法也相对复杂,所以文中没有仔 ...

  4. Scrum会议（第十一周）

    十一周会议 1.任务分配: github相关代码 2.会议记录: 总结并阐述了自己在上周存在的问题以及解决了自己把自己的issue发在了自己的github,并没有把问题发在我们项目小组的项目的issu ...

  5. OpenFOAM——过渡管中的湍流

    本算例来自<ANSYS Fluid Dynamics Verification Manual>中的VMFL016:Turbulent Flow in a Transition Duct 一 ...

  6. 创建workbook及相关操作

    通过openpyxl模块创建workbook时,无需本地事先创建好excel,它会直接创建一个新的excel文件 创建workbook时,会至少包含一个worksheet 注意:openpyxl模块只 ...

  7. LeetCode 202: 快乐数 Happy Number

    题目: 编写一个算法来判断一个数是不是 "快乐数". 一个 "快乐数" 定义为:对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和,然后重复这个过程直 ...

  8. 《细说PHP》第四版 样章 第23章 自定义PHP接口规范 1

    如今的项目开发中,接口是很普遍的应用技术.现在好多项目组都单独设有接口开发人员.像腾讯.微博.淘宝等开放平台,其所谓的开放,就是提供一些可调用的接口,用于获取相关的信息.例如,微信用户基本信息.淘宝店 ...

  9. 纯手打AJAX，还有一个对象转查询字符串的小方法obj=>url

    function json2url(json){ var arr=[]; for(var name in json){ arr.push(name+'='+json[name]); } return ...

  10. copy_from/to_user详解

    参考:http://www.wowotech.net/memory_management/454.html 宋大侠的文章精彩,郭大侠的评论也精彩. 结论简单摘录如下: 无论是内核态还是用户态访问合法的 ...