Python线性回归算法【解析解，sklearn机器学习库】

一.概述

　　参考博客：https://www.cnblogs.com/yszd/p/8529704.html

二.代码实现【解析解】

 import numpy as np
 import matplotlib.pyplot as plt

 __author__ = 'zhen'

 # 这里相当于是随机X维度X1，rand是随机均匀分布
 X = 2 * np.random.rand(100, 1)
 # 人为的设置真实的Y一列，np.random.randn(100, 1)是设置error，randn是标准正太分布
 y = 3 + 6 * X + np.random.randn(100, 1)
 # 整合X0和X1
 X_b = np.c_[np.ones((100, 1)), X] #combine聚合两数据集
 # print(X_b)

 # 常规等式求解theta
 # invert
 theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
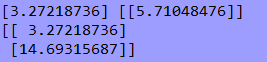
 print(theta_best)

 # 创建测试集里面的X1
 X_new = np.array([[0], [2]])
 X_new_b = np.c_[(np.ones((2, 1))), X_new]
 print(X_new_b)
 y_predict = X_new_b.dot(theta_best)
 print(y_predict)

 plt.plot(X_new, y_predict, 'r-')
 plt.plot(X, y, 'b.')
 plt.axis([0, 2, 0, 15])
 plt.show()

三.结果【解析解】

　　

　　可视化：

　　

四.代码实现【sklearn机器学习库】

 import numpy as np
 import matplotlib.pyplot as plt
 from sklearn.linear_model import LinearRegression

 __author__ = 'zhen'

 X = 2 * np.random.rand(100, 1)
 y = 3 + 6 * X + np.random.randn(100, 1)

 lin_reg = LinearRegression()
 lin_reg.fit(X, y)
 print(lin_reg.intercept_, lin_reg.coef_)

 X_new = np.array([[0], [2]])
 y_predict = lin_reg.predict(X_new)
 print(y_predict)

 # 可视化
 plt.plot(X_new, y_predict, 'r-')
 plt.plot(X, y, 'b.')
 plt.axis([0, 2, 0, 15])
 plt.show()

五.结果【sklearn机器学习库】

　　

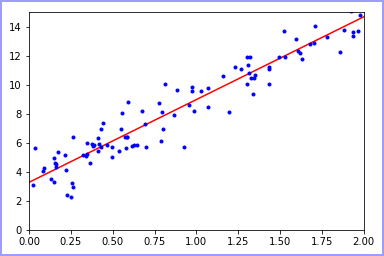
　　可视化：

　　

六.总结

　　根据图示可以得出结论，使用解析解或者是sklearn机器学习库都可以得到大致的结论，所花费时间和达到的效率都比较类似。但这仅限于一元线性回归，当参数类别增加时，使用解析解会大大增加程序复杂程度和计算耗能，因此建议多使用sklearn库，并根据情况进行参数配置和优化。