[luoguP1578] 奶牛浴场（DP）

传送门

O(s²)算法

详见论文 王知昆--浅谈用极大化思想解决最大子矩形问题

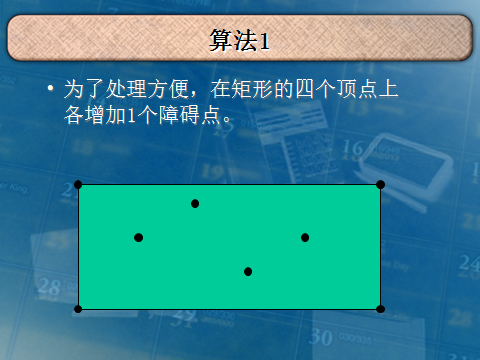
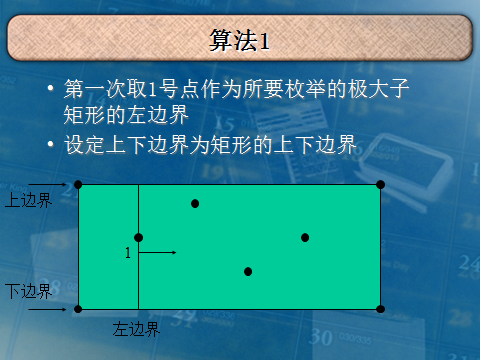
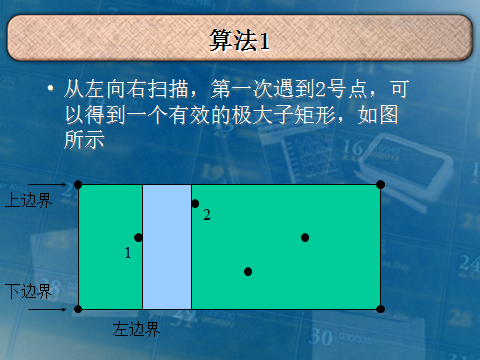
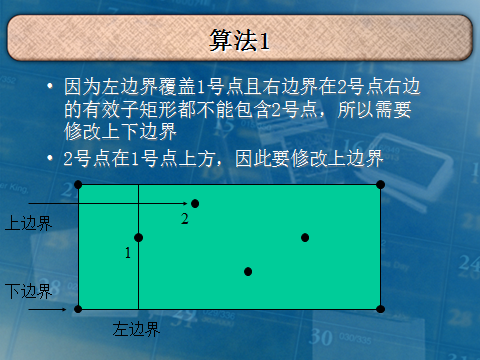
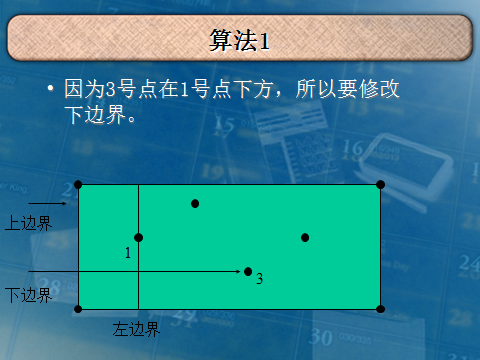
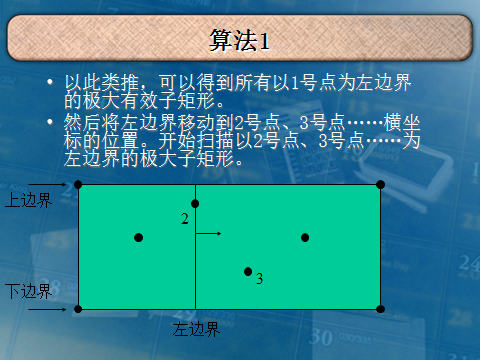
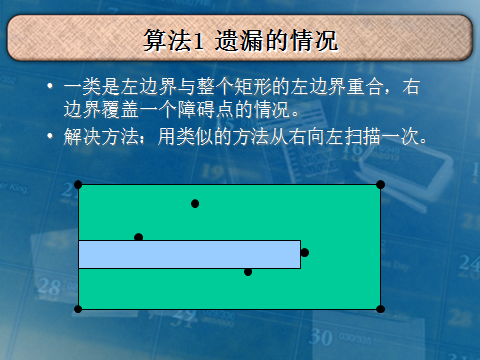
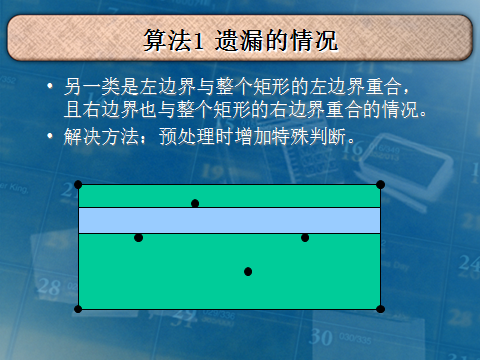
我就复制你能把我怎么样QAQ

#include <cstdio>
#include <iostream>
#include <algorithm>
#define N 5010
#define max(x, y) ((x) > (y) ? (x) : (y))
#define min(x, y) ((x) < (y) ? (x) : (y))

int L, W, n, ans;
struct node
{
	int x, y;
}p[N];

inline int read()
{
	int x = 0, f = 1;
	char ch = getchar();
	for(; !isdigit(ch); ch = getchar()) if(ch == '-') f = -1;
	for(; isdigit(ch); ch = getchar()) x = (x << 1) + (x << 3) + ch - '0';
	return x * f;
}

inline bool cmp1(node a, node b)
{
	return a.y < b.y;
}

inline bool cmp2(node a, node b)
{
	return a.x < b.x;
}

int main()
{
	int i, j, x, u, d;
	L = read();
	W = read();
	n = read();
	for(i = 1; i <= n; i++) p[i].x = read(), p[i].y = read();
	p[++n].x = 0, p[n].y = 0;
	p[++n].x = 0, p[n].y = W;
	p[++n].x = L, p[n].y = 0;
	p[++n].x = L, p[n].y = W;
	std::sort(p + 1, p + n + 1, cmp1);
	for(i = 2; i <= n; i++)
	{
		x = p[i].y - p[i - 1].y;
		ans = max(ans, x * L);
	}
	std::sort(p + 1, p + n + 1, cmp2);
	for(i = 1; i <= n; i++)
	{
		u = W;
		d = 0;
		for(j = i + 1; j <= n; j++)
		{
			if(p[j].x == p[i].x) continue;
			ans = max(ans, (u - d) * (p[j].x - p[i].x));
			if(p[j].y == p[i].y)
			{
				if(u - p[j].y > p[j].y - d) d = p[j].y;
				else u = p[j].y;
			}
			else
			{
				if(p[j].y > p[i].y) u = min(u, p[j].y);
				else d = max(d, p[j].y);
			}
		}
	}
	for(i = n; i >= 1; i--)
	{
		u = W;
		d = 0;
		for(j = i - 1; j >= 1; j--)
		{
			if(p[j].x == p[i].x) continue;
			ans = max(ans, (u - d) * (p[j].x - p[i].x));
			if(p[j].y == p[i].y)
			{
				if(u - p[j].y > p[j].y - d) d = p[j].y;
				else u = p[j].y;
			}
			else
			{
				if(p[j].y > p[i].y) u = min(u, p[j].y);
				else d = max(d, p[j].y);
			}
		}
	}
	printf("%d\n", ans);
	return 0;
}