Java实验——输出二维数组连续二维子数组的最大和
该算法思路,根据我博客里面一维子数组求和的思路,可以用一个新的二维数组对该二维区域的数组进行求和,例如新的二维数组的第5个位置,就代表从1到5斜对角线的块状区域的和,即1,2,4,5这4个数的和,x个位置表示从1到x的斜对角块状区域的和,利用循环一一求出对应的和,一次循环即可,这个循环复杂度为O(nm)
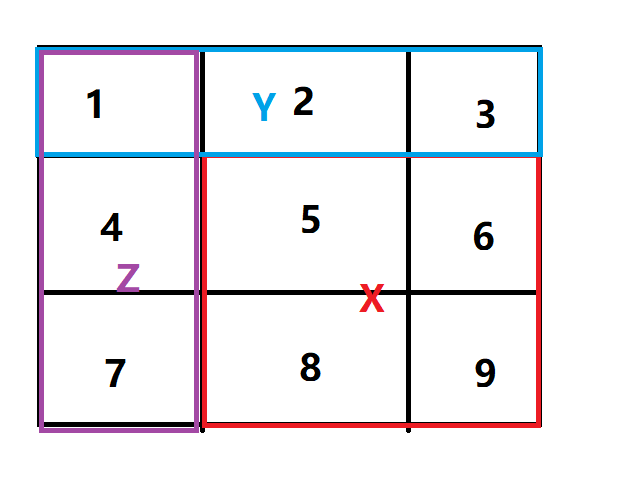
接着再求出来新的二维数组中,每一个从1到X的块状区域的和均被求出,所以对于任意区域X(如图以具体的例子展示出来),只需要求出其最大值即可。
确定一个点需要两层循环,即循环O(mn),在二维数组中需要求两个点,所以复杂度为O(m2n2)。
求值分3种(或者说4种),第1种情况即从1到X区域有最大值,这种情况在上面求和的过程中已经求出最大,所以再进行考虑。
除了不再考虑的情况,第1种最常见的情况是:
对于任意区域X要求和,只需要获得新的数组X区域右下角的值(第9个数据的值),减去Z区域的右下角的值(第7个数据),减去Y区域右下角的值(第3个数据),加上Z交Y右下角的值即可(第1个数据)。
第2种情况是块状区域包含第一行的时候有最大值,只需要求出获得X区域右下角的值减去Z区域右下角的值最大就行了
第3种情况是块状区域包含第一列的时候有最大值,只需要求出获得X区域右下角的值减去Y区域右下角的值最大就行了
根据上述的条件,实现了以下的算法如下:
package lianxu1; import java.io.IOException;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List; public class ShowSub { public static void main(String[] args) throws IOException {
Integer c[][]= {
{1,2,-3,-1,2,2},
{-3,4,5,1,-1,3},
{-2,-3,4,1,4,3}
};
//求和
List<List<Integer>> main=new ArrayList<List<Integer>>();
for(int i=0;i<c.length;i++)
{
List<Integer> heng=new ArrayList<Integer>();
for(int j=0;j<c[0].length;j++)
{
if(j!=0)
heng.add(c[i][j]+heng.get(j-1));
else heng.add(c[i][j]);
}
if(i!=0)
main.add(addList(heng,main.get(i-1)));
else main.add(heng);
}
//求最大值 int max=main.get(0).get(0);
for(int z=0;z<main.size();z++)
{
int temp=Collections.max(main.get(z));
if(max<temp)
{
max=temp;
}
}
//确定一位置
for(int i1=0;i1<main.size();i1++)
{
for(int j1=0;j1<main.get(0).size();j1++)
{
//确定二位置
for(int i2=i1+1;i2<main.size();i2++)
{
for(int j2=j1+1;j2<main.get(0).size();j2++)
{
int g_max=0;
if(i1!=0&&j1!=0)
{
g_max=(main.get(i2).get(j2)+main.get(i1-1).get(j1-1)-main.get(i2).get(j1-1)-main.get(i1-1).get(j2)); }
else if(i1!=0)
{
g_max=(main.get(i2).get(j2)-main.get(i1-1).get(j2));
}
else if(j1!=0)
{
g_max=(main.get(i2).get(j2)-main.get(i2).get(j1-1));
}
if(max<g_max)
{
max=g_max;
}
}
}
}
}
System.out.println("该二维数组整理区域和为:"+main);
System.out.println("该二维数组最大块区域和为:"+max);
}
public static List<Integer> addList(List<Integer> a,List<Integer> b)
{
List<Integer> sum=new ArrayList<Integer>();
for(int i=0;i<a.size();i++)
{
sum.add(a.get(i)+b.get(i));
}
// for(int i1=0;i1<a.size();i1++)
// {
// sum.set(i1,sum.get(i1)+b.get(i1));
// }
return sum;
} }
根据这个二维数组:

结果如下所示:
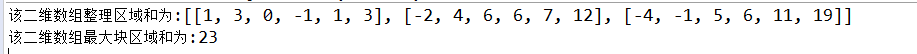
Java实验——输出二维数组连续二维子数组的最大和的更多相关文章
- 连续子数组的最大乘积及连续子数组的最大和(Java)
1. 子数组的最大和 输入一个整形数组,数组里有正数也有负数.数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和.求所有子数组的和的最大值.例如数组:arr[]={1, 2, 3, -2, ...
- 【Java学习笔记之八】java二维数组及其多维数组的内存应用拓展延伸
多维数组声明 数据类型[][] 数组名称; 数据类型[] 数组名称[]; 数据类型数组名称[][]; 以上三种语法在声明二维数组时的功能是等价的.同理,声明三维数组时需要三对中括号,中括号的位置可以在 ...
- “全栈2019”Java第三十一章:二维数组和多维数组详解
难度 初级 学习时间 10分钟 适合人群 零基础 开发语言 Java 开发环境 JDK v11 IntelliJ IDEA v2018.3 文章原文链接 "全栈2019"Java第 ...
- 【Java学习笔记之九】java二维数组及其多维数组的内存应用拓展延伸
多维数组声明 数据类型[][] 数组名称; 数据类型[] 数组名称[]; 数据类型数组名称[][]; 以上三种语法在声明二维数组时的功能是等价的.同理,声明三维数组时需要三对中括号,中括号的位置可以在 ...
- 062 01 Android 零基础入门 01 Java基础语法 07 Java二维数组 01 二维数组应用
062 01 Android 零基础入门 01 Java基础语法 07 Java二维数组 01 二维数组应用 本文知识点:二维数组应用 二维数组的声明和创建 ? 出现空指针异常 数组的名字指向数组的第 ...
- c# 一维数组,二维数组,多维数组。
数组就是给一个变量定义多个字符,可以是string也可以是int.或者说是一组变量. 可以更加方便的操作大量数据. 数组的定义1.数组里面的内容必须是同一类型2.数据必须有长度限制 一维数组 *一.数 ...
- C# 数组、一维数组、二维数组、多维数组、锯齿数组
C# 数组.一维数组.二维数组.多维数组.锯齿数组 一.数组: 如果需要使用同一类型的对象,就可以使用数组,数组是一种数据结构,它可以包含同一类型的多个元素.它的长度是固定的,如长度未知的情况下,请 ...
- c#简单实现二维数组和二维数组列表List<>的转置
刚看到网上一篇文章里用sql实现了行列转置.sql server 2005/2008只用一个pivot函数就可以实现sql server 2000很多行的复杂实现.提到转置,立刻想起还在求学阶段曾经做 ...
- java:集合输出之Iterator和ListIterator二
java:集合输出之Iterator和ListIterator二 ListIterator是Iterator的子接口,Iterator的最大特点是,能向前,或向后迭代.如果现在要想双向输出的话,则只能 ...
随机推荐
- Traceroute侦测主机到目的主机之间所经路由情况的重要工具
ICMP的应用--Traceroute Traceroute是用来侦测主机到目的主机之间所经路由情况的重要工具,也是最便利的工具.前面说到,尽管ping工具也可以进行侦测,但是,因为ip头的限制,pi ...
- DECLARE - 定义一个游标
SYNOPSIS DECLARE name [ BINARY ] [ INSENSITIVE ] [ [ NO ] SCROLL ] CURSOR [ { WITH | WITHOUT } HOLD ...
- uva10735 Euler Circuit
题外话:很多混合图问题可以转化为有向图问题(将无向边拆为两条有向边) 本题不行,因为只能经过一次 这种问题能想到网络流.. 复习欧拉回路:入度==出度 和uva1380有点相似,要先给无向边定向.原图 ...
- NetBeans 默认编码修改方法
如果要NetBeans用UTF-8对文件进行解码,需要修改配置文件,具体方法如下: 1. 找到你的Netbeans安装目录下的etc文件夹,如D:\Program Files\NetBeans 8.2 ...
- Linux OOM-killer 内存不足时kill高内存进程的策略
OOM_killer是Linux自我保护的方式,当内存不足时不至于出现太严重问题,有点壮士断腕的意味 在kernel 2.6,内存不足将唤醒oom_killer,挑出/proc/<pid> ...
- modify django app models.py adn settings.py
from django.db import models from django.contrib import admin # from personal import models class Us ...
- Sphinx排序模式
目前SPHINX支持6种排序模式.分别是: 1. SPH_SORT_RELEVANCE2. SPH_SORT_ATTR_DESC3. SPH_SORT_ATTR_ASC4. SPH_SORT_TIME ...
- 删除mysql中user为空用户,mysql空密码
进入mysql数据库 mysql -uroot -p 查看用户信息 select user,host ,Password from mysql.user; 如下图: 删除user为空用户 delete ...
- Linux网络技术管理
1. OSI七层模型和TCP/IP四层模型 1.1 osi 七层模型 Open System interconnection,开放系统互连参考模型是国际标准化组织(ISO)制定的一个用于计算机或通信系 ...
- Linux基础学习-命令行与图形界面切换
命令行模式和图形界面模式切换 打开文件 vim /etc/inittab # systemd uses 'targets' instead of runlevels. By default, ther ...
