SP1805 Largest Rectangle in a Histogram

题目链接：###

洛谷SP1805

题意：###

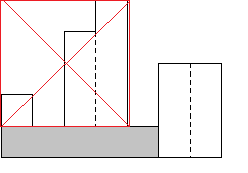
 如图所示，在一条水平线上有n个宽为1的矩形，求包含于这些矩形的最大子矩形面积（图中的阴影部分的面积即所求答案）

输入格式：

   有多组测试数据，每组数据占一行。输入零时读入结束。

   每行开头为一个数字n（1<=n<=100000）,接下来在同一行给出n个数字h1h2...hn（0<=hi<=1000000000）表示每个矩形的高度。

输出格式：

   对于每组数据，输出最大子矩阵面积，一组数据输出一行。

题目分析：###

一道单调栈的典型例题……

如果矩形高度单增，可以用每个矩形的高度*从这个矩形到最右边的距离得到一个值，然后取最大的就是ans

如果矩形高度不单调，显然因为右边有比这个矩形高度更矮的矩形所以这个矩形的高度并没有什么卵用

这个时候前面那些矩形除了宽度已经没什么用了，记一下宽度果断丢掉（丢的时候记宽度，并乘高度以更新答案），然后这样矩形序列就又单增啦

用单调栈实现，边读边做，每次把比当前矩形高的都弹出来，然后把当前矩形入栈

最后还要仿照之前的做法把剩下的弹出来更新答案，栈空结束算法，输出答案

---

代码：###

#include<bits/stdc++.h>
#define MAXN (100000+5)
using namespace std;
inline int read(){
	int f=1,cnt=0;char c;
	c=getchar();
	while(!isdigit(c)){if(c=='-')f=-f;c=getchar();}
	while(isdigit(c)){cnt=cnt*10+c-'0';c=getchar();}
	return cnt*f;
}
int sta[MAXN],w[MAXN],x;
int n,top=0;
long long ans=0;
int main(){
	while(1){
		top=0;ans=0;
		n=read();if(n==0)return 0;
		sta[0]=0;
		for(register int i=1;i<=n;i++)w[i]=sta[i]=0;
		for(register int i=1;i<=n;i++){
			x=read();
			if(x>=sta[top]){
				sta[++top]=x;
				w[top]=1;
			}
			else{
				int tot=0;
				while(sta[top]>x){
					tot+=w[top];
					ans=max(ans,(long long)tot*sta[top]);
					top--;
				}
				sta[++top]=x;w[top]=tot+1;
			}
		}
		int tot=0;
		while(top){
			tot+=w[top];
			ans=max(ans,(long long)tot*sta[top]);
			top--;
		}
		printf("%lld\n",ans);
//		for(register int i=1;i<=n;i++)printf("%d ",sta[i]);
	}
	return 0;
}