svm中的数学和算法
支持向量机(Support Vector Machine)是Cortes和Vapnik于1995年首先提出的,它在解决小样本、非线性及高维模式识别中表现出很多特有的优势,并可以推广应用到函数拟合等其它机器学习问题中。
一、数学部分
1.1二维空间
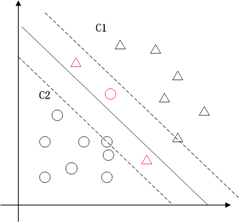
支持向量机的典型应用是分类,用于解决这种问题:有一些事物是能够被分类的,可是详细怎么分类的我们又说不清楚,比方说下图中三角的就是C1类,圆圈的就是C2类,这都是已知的,好,又来了一个方块,这个方块是属于C1呢还是属于C2呢,说不清楚。SVM算法就是试着帮您把这件事情说清楚的。
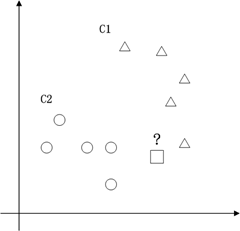 在二维空间里(这时候样本有两个參照属性),SVM就是在C1和C2中间划一条线g(x)=0,线儿上边的属于C1类,线儿下边的属于C2类,这时候方块再来,咱就有章程了。
在二维空间里(这时候样本有两个參照属性),SVM就是在C1和C2中间划一条线g(x)=0,线儿上边的属于C1类,线儿下边的属于C2类,这时候方块再来,咱就有章程了。
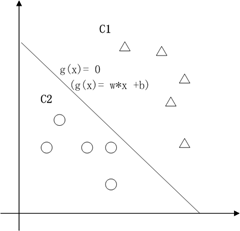
关于g(x) = 0得再啰嗦几句,g(x)里边的x不是横坐标,而是一个向量,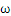 也不是解析几何里边的斜率,也是向量。
也不是解析几何里边的斜率,也是向量。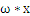 是一个向量积。比方在解析几何意义上的直线y = -x-b,换成向量表示法就是
是一个向量积。比方在解析几何意义上的直线y = -x-b,换成向量表示法就是 ,这里w就是那个
,这里w就是那个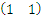 ,x就是那个
,x就是那个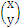 。
。
对C1类中的点:g(x) > 0;对于 C2类中的点:g(x) < 0 ;
假设我们用y来表示类型,+1代表C1类,-1代表C2类。
那么对于全部训练样本而言,都有: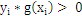 ,那么g(x) = 0 就行正确切割全部训练样本的那条线,仅仅要把g(x) = 0这条线给找出来就能凑合用了。
,那么g(x) = 0 就行正确切割全部训练样本的那条线,仅仅要把g(x) = 0这条线给找出来就能凑合用了。
这也就仅仅能凑合用,由于满足这个条件的g(x) = 0 太多了,追求完美的我们要的是最优的那条线。怎么才是最优的呢?直觉告诉我们g(x) = 0这条线不偏向C1那边,也不偏向C2那边,就应该是最优的了吧。对,学名叫分类间隔,下图红线的长度就是分类间隔。
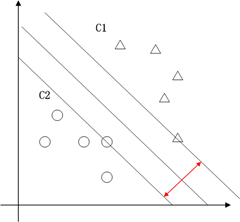
在二维空间中,求分类间隔,能够转化为求点到线的距离,点到线的距离能够表示为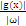 (向量表示)。为简单计,把整个二维空间归一化(等比放大或缩小),使得对于全部的样本,都有|g(x)|>=1,也就是让C1和C2类中离g(x)=0近期的训练样本的|g(x)|=1,这时分类间隔就是
(向量表示)。为简单计,把整个二维空间归一化(等比放大或缩小),使得对于全部的样本,都有|g(x)|>=1,也就是让C1和C2类中离g(x)=0近期的训练样本的|g(x)|=1,这时分类间隔就是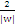 ,这个间隔越大越好,那么|
,这个间隔越大越好,那么|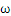 |越小越好。
|越小越好。
1.2多维空间
如今我们已经在2维空间中抽象出一个数学问题,求满足例如以下条件的g(x)=0:
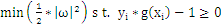 ,即在满足
,即在满足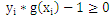 条件下能使
条件下能使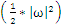 取最小值的那个w。在二维空间中,w能够近似的理解为斜率,在样本确定,斜率确定的情况下,
取最小值的那个w。在二维空间中,w能够近似的理解为斜率,在样本确定,斜率确定的情况下,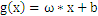 中的那个b也是能够确定的,整个
中的那个b也是能够确定的,整个 = 0也就确定了。
= 0也就确定了。
如今我们讨论的仅仅是二维空间,可是我们惊喜的发现,在二维空间中的结论能够非常easy的推广到多维空间。比方说:
我们仍然能够把多维空间中的切割面(超平面)表示为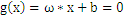 。
。
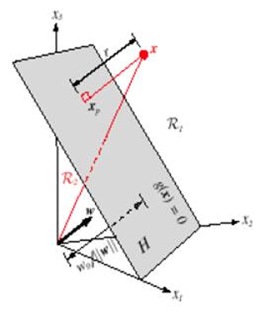
多维空间中点到面的距离仍然能够表示为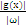 。例如以下图,平面表示为
。例如以下图,平面表示为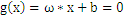 ,x是
,x是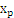 在面上的投影,r是x到面的距离,简单推导例如以下:
在面上的投影,r是x到面的距离,简单推导例如以下:
w向量垂直于平面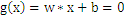 ,有:
,有: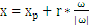 ,把上式带入
,把上式带入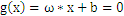 中得到
中得到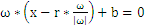 ,化简得到
,化简得到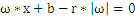 ,所以
,所以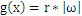 ,向量x到平面
,向量x到平面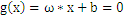 的距离
的距离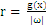 ,这和二维空间中结论也是一致的。
,这和二维空间中结论也是一致的。
如今我们把SVM从2维空间推广到多维空间,即求满足例如以下条件的g(x)=0:
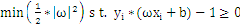 。
。
1.3拉格朗日因子
这是一个典型的带约束条件的求极值问题,目标函数是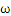 的二次函数,约束函数是
的二次函数,约束函数是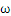 的线性函数:二次规划问题。求解二次规划问题的一般性方法就是加入拉格朗日乘子,构造拉格朗日函数(理论上这儿应该另一些额外的数学条件,拉格朗日法才是可用,就略过了)。
的线性函数:二次规划问题。求解二次规划问题的一般性方法就是加入拉格朗日乘子,构造拉格朗日函数(理论上这儿应该另一些额外的数学条件,拉格朗日法才是可用,就略过了)。
详细求解过程例如以下:
1、构造拉格朗日函数
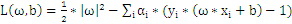
当中 和b是未知量。
和b是未知量。
2、对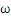 和b求偏导数,令偏导数为0。
和b求偏导数,令偏导数为0。
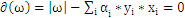 , 即
, 即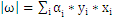
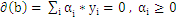
3、把上式带回拉格朗日函数,得到拉格朗日对偶问题,把问题转化为求解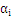
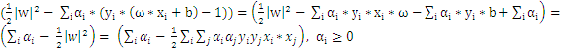
4、最后把问题转化为求解满足下列等式的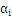
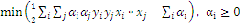
1.4线性化
好,如今我们再来梳理一下svm的分类逻辑,在空间中找一个切割面(线)把样本点分开,切割面(线)的最优条件就是分类间隔最大化,分类间隔是基于点到平面(直线)的距离来计算的。问题是全部的切割面都是平面,全部的切割线都是直线吗?显然不是。
比方特征是房子的面积x,这里的x是实数,结果y是房子的价格。如果我们从样本点的分布中看到x和y符合3次曲线,那么我们希望使用x的三次多项式来逼近这些样本点。
在二维空间中这是非线性的,这样我们前面的推理都没法用了------点到曲线的距离?不知道怎么算。可是假设把x映射到3维空间 ,那么对于
,那么对于 来说,
来说, 就是线性的,也就是说,对于低维空间中非线性的线(面),在映射到高维空间中时,就能变成线性的。于是我们还须要把问题做一个小小的修正,我们面临的问题是求解:
就是线性的,也就是说,对于低维空间中非线性的线(面),在映射到高维空间中时,就能变成线性的。于是我们还须要把问题做一个小小的修正,我们面临的问题是求解:
 ,这里面引入了一个Kernel,核函数,用于样本空间的线性化。
,这里面引入了一个Kernel,核函数,用于样本空间的线性化。
1.5松弛变量
上面就是一个比較完整的推导过程,可是经验表明把上述条件丢给计算机进行求解,基本上是无解的,由于条件太苛刻了。实际上,最常常出现的情况例如以下图红色部分,在分类过程中会出现噪声,假设对噪声零容忍那么非常有可能导致分类无解。
为了解决问题又引入了松弛变量。把原始问题修正为:
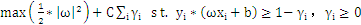
依照拉格朗日法引入拉格朗日因子:
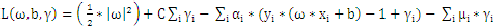
对上式分别求 的导数得到:
的导数得到:
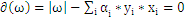 , 即
, 即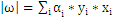
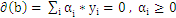
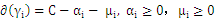
带回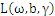 得到拉格朗日的对偶问题:
得到拉格朗日的对偶问题:
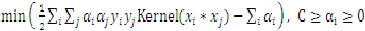
另外当目标函数取极值时,约束条件一定是位于约束边界(KKT条件),也就是说:
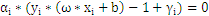
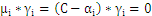
分析上面式子能够得出下面结论:
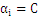 时:
时: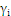 能够不为零,就是说该点到切割面的距离小于
能够不为零,就是说该点到切割面的距离小于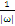 ,是误分点。
,是误分点。
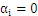 时:
时: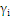 为零,
为零,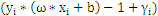 大于零:表示该点到切割面的距离大于
大于零:表示该点到切割面的距离大于 是正确分类点。
是正确分类点。
 时:
时: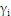 为零,
为零, ,该点就是支持向量。
,该点就是支持向量。
再用数学语言提炼一下:
令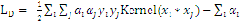 ,其对
,其对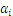 的偏导数为:
的偏导数为:
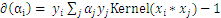 。
。
KKT条件能够表示为:
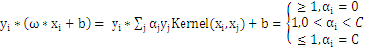
用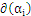 表示该KKT条件就是:
表示该KKT条件就是:
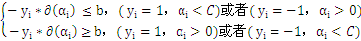
若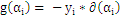 ,则
,则
全部的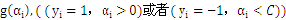 大于全部的
大于全部的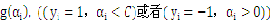 。这里b作为中间数被忽略了,由于b是能够由
。这里b作为中间数被忽略了,由于b是能够由 推导得到的。
推导得到的。
二、算法部分
对于样本数量比較多的时候(几千个),SVM所须要的内存是计算机所不能承受的。眼下,对于这个问题的解决方法主要有两种:块算法和分解算法。这里,libSVM採用的是分解算法中的SMO(串行最小化)方法,其每次训练都仅仅选择两个样本。基本流程例如以下:
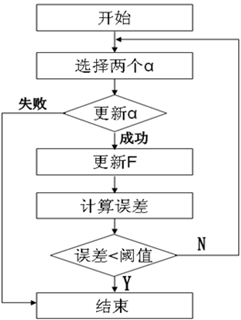
这里有两个重要的算法,一个是 的选择,还有一个是
的选择,还有一个是 的更新。
的更新。
2.1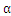 的选择算法
的选择算法
选择两个和KKT条件违背的最严重的两个 ,包括两层循环:
,包括两层循环:
外层循环:优先选择遍历非边界样本,由于非边界样本更有可能须要调整,而边界样本经常不能得到进一步调整而留在边界上。在遍历过程中找出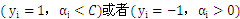 的全部样本中
的全部样本中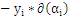 值最大的那个(这个样本是最有可能不满足
值最大的那个(这个样本是最有可能不满足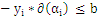 条件的样本。
条件的样本。
内层循环:对于外层循环中选定的那个样本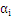 ,找到这种样本
,找到这种样本 ,使得:
,使得:
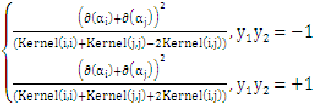
 最大,上式是更新
最大,上式是更新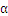 中的一个算式,表示的是在选定
中的一个算式,表示的是在选定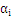 ,
,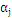 最为更新算子的情况下,
最为更新算子的情况下,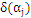 最大。
最大。
假设选择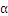 的过程中发现KKT条件已经满足了,那么算法结束。
的过程中发现KKT条件已经满足了,那么算法结束。
2.2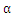 的更新算法
的更新算法
因为SMO每次都仅仅选择2个样本,那么等式约束能够转化为直线约束:
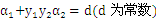
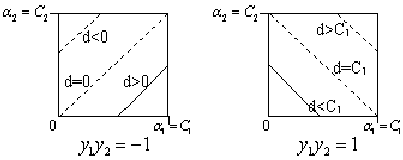
转化为图形表示为:
那么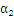 的取值范围是:
的取值范围是:
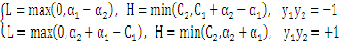
把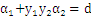 带入
带入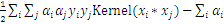 中,得到一个一元二次方程,求极值得到:
中,得到一个一元二次方程,求极值得到:
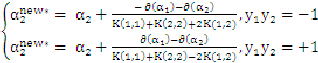
终于:
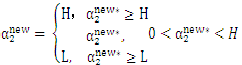
2.3其它
上面说到SVM用到的内存巨大,还有一个缺陷就是计算速度,由于数据大了,计算量也就大,非常显然计算速度就会下降。因此,一个好的方式就是在计算过程中逐步去掉不參与计算的数据。由于,实践证明,在训练过程中,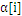 一旦达到边界(
一旦达到边界(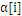 =0或者
=0或者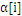 =C),
=C), 的值就不会变,随着训练的进行,參与运算的样本会越来越少,SVM终于结果的支持向量(0<
的值就不会变,随着训练的进行,參与运算的样本会越来越少,SVM终于结果的支持向量(0<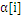
LibSVM採用的策略是在计算过程中,检測active_size中的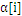 值,假设
值,假设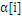 到了边界,那么就应该把对应的样本去掉(变成inactived),并放到栈的尾部,从而逐步缩小active_size的大小。
到了边界,那么就应该把对应的样本去掉(变成inactived),并放到栈的尾部,从而逐步缩小active_size的大小。
b的计算 ,基本计算公式为:
理论上,b的值是不定的。当程序达到最优后,仅仅要用随意一个标准支持向量机(0<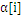 <C)的样本带入上式,得到的b值都是能够的。眼下,求b的方法也有非常多种。在libSVM中,分别对y=+1和y=-1的两类全部支持向量求b,然后取平均值。
<C)的样本带入上式,得到的b值都是能够的。眼下,求b的方法也有非常多种。在libSVM中,分别对y=+1和y=-1的两类全部支持向量求b,然后取平均值。
svm中的数学和算法的更多相关文章
- 借One-Class-SVM回顾SMO在SVM中的数学推导--记录毕业论文5
上篇记录了一些决策树算法,这篇是借OC-SVM填回SMO在SVM中的数学推导这个坑. 参考文献: http://research.microsoft.com/pubs/69644/tr-98-14.p ...
- SVM中图像常用的HOG特征描述及实现
转摘网址:http://www.cnblogs.com/tiandsp/archive/2013/05/24/3097503.html Hog参考网址:http://www.cnblogs.com/t ...
- 再生核希尔伯特空间(RKHS)在监督学习(SVM)中的应用
[转载请注明出处]http://www.cnblogs.com/mashiqi 2014/4/10 在网上找到一个讲reproducing kernel的tutorial看了一看,下面介绍一下. 首先 ...
- word2vec中的数学原理一 目录和前言
最近在看词向量了,因为这个概念对于语言模型,nlp都比较重要,要好好的学习一下.把网上的一些资料整合一下,搞个系列. 主要参考: word2vec 中的数学原理详解 ...
- SVM中为何间隔边界的值为正负1
在WB二面中,问到让讲一下SVM算法. 我回答的时候,直接答道线性分隔面将样本分为正负两类,取平行于线性切割面的两个面作为间隔边界,分别为:wx+b=1和wx+ b = -1. 面试官就问,为什么是正 ...
- 图像处理中的数学原理具体解释21——PCA实例与图像编码
欢迎关注我的博客专栏"图像处理中的数学原理具体解释" 全文文件夹请见 图像处理中的数学原理具体解释(总纲) http://blog.csdn.net/baimafujinji/ar ...
- sklearn中调用集成学习算法
1.集成学习是指对于同一个基础数据集使用不同的机器学习算法进行训练,最后结合不同的算法给出的意见进行决策,这个方法兼顾了许多算法的"意见",比较全面,因此在机器学习领域也使用地非常 ...
- Spark/Scala实现推荐系统中的相似度算法(欧几里得距离、皮尔逊相关系数、余弦相似度:附实现代码)
在推荐系统中,协同过滤算法是应用较多的,具体又主要划分为基于用户和基于物品的协同过滤算法,核心点就是基于"一个人"或"一件物品",根据这个人或物品所具有的属性, ...
- Java中常用的查找算法——顺序查找和二分查找
Java中常用的查找算法——顺序查找和二分查找 神话丿小王子的博客 一.顺序查找: a) 原理:顺序查找就是按顺序从头到尾依次往下查找,找到数据,则提前结束查找,找不到便一直查找下去,直到数据最后一位 ...
随机推荐
- 转(havel 算法)
http://www.cnblogs.com/wally/p/3281361.html poj 1659(havel算法) 题目链接:http://poj.org/problem?id=1659 思路 ...
- 点击链接直接跳转到 App Store 指定应用下载页面
//跳转到应用页面 NSString *str = [NSString stringWithFormat:@"http://itunes.apple.com/us/app/id%d" ...
- N种方法妙讲LIS算法
LIS算法经典汇总 假设存在一个序列d[1..9] = 2 1 5 3 6 4 8 9 7,可以看出来它的LIS长度为5.下面一步一步试着找出它.我们定义一个序列B,然后令 i = 1 to 9 逐个 ...
- 在opensips中记录通话记录
1.为acc表增加额外的字段记录主叫被叫进入mysql,选取opensips的数据库ALTER TABLE acc ADD from_uri VARCHAR(64) DEFAULT '' NOT NU ...
- 基于redis AE异步网络架构
最近的研究已redis源代码,redis高效率是令人钦佩. 在我们的linux那个机器,cpu型号, Intel(R) Pentium(R) CPU G630 @ 2.70GHz Intel(R) ...
- Javascript进阶篇——(函数)笔记整理
这节是根据慕课网和JavaScript DOM编程艺术一书加起来做的笔记 什么是函数如果需要多次使用同一段代码,可以把它们封装成一个函数.函数(function)就是一组允许在你的代码里随时调用的语句 ...
- jquery方法详解
jquery方法详解 http://www.365mini.com/doc
- WCF方式调用asmx设置cookie
以前旧的方式去调用web service, 可以通过CookieContainer去设置cookie,改用WCF方式去调用,则必须配置allowCookies属性为true <system.se ...
- 获取设备的UUID
很多时候需要获取设备的UUID,比如在蓝牙交互时,需要获取服务和特征的UUID,那么如何获取设备的UUID呢?请见如下代码: // // ViewController.m // 获取UUID // / ...
- IOS--工作总结--post上传文件(以流的方式上传)
1.添加协议 <NSURLConnectionDelegate> 2.创建 @property (nonatomic,retain) NSURLConnection* aSynConnec ...
