LightOJ - 1297 Largest Box LightOJ（一元三次方程求极大值）

题目链接：https://vjudge.net/contest/28079#problem/K

题目大意：给你一个长为L，宽为W的纸片，四个角剪掉边长为x的正方形，如下图所示，然后折成一个无盖的纸盒，求纸盒最大体积。

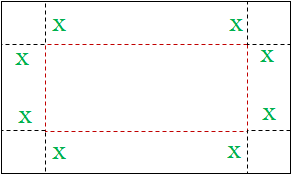
解题思路：我们可以知道体积V(x)=(L-2*x)*(W-2*x)*x求导得到f(x)=12x^2-4*(L+W)*x^2+L*W，V(x)的图像如下所示

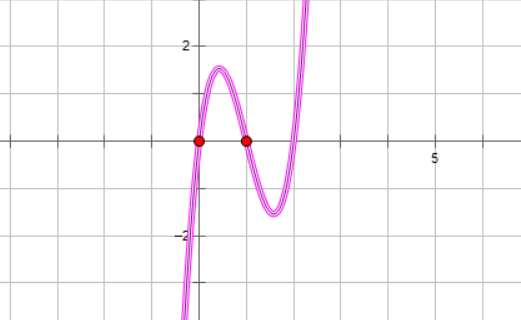
所以我们知道极大值点是f(x)两个（或一个）零点中x值较小的那个点,可以通过求根公式求得。

代码：

 #include<iostream>
 #include<stdio.h>
 #include<cmath>
 using namespace std;

 double L,W;

 double fun(double x){
     return x*(L-*x)*(W-*x);
 }

 int main(){
     int T;
     scanf("%d",&T);
     int cas=;
     while(T--){
         scanf("%lf%lf",&L,&W);
         double pos=(*(L+W)-sqrt(*(L+W)*(L+W)-**L*W))/24.0;
         printf("Case %d: %lf\n",++cas,fun(pos));
     }
 }