深度学习基础系列（三）| sigmoid、tanh和relu激活函数的直观解释

　　常见的激活函数有sigmoid、tanh和relu三种非线性函数，其数学表达式分别为：

• sigmoid: y = 1/(1 + e^-x)
• tanh: y = (e^x - e^-x)/(e^x + e^-x)
• relu: y = max(0, x)

　　其代码实现如下：

import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def tanh(x):
    return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))

def relu(x):
    return np.maximum(0, x)

x = np.arange(-5, 5, 0.1)
p1 = plt.subplot(311)
y = tanh(x)
p1.plot(x, y)
p1.set_title('tanh')
p1.axhline(ls='--', color='r')
p1.axvline(ls='--', color='r')

p2 = plt.subplot(312)
y = sigmoid(x)
p2.plot(x, y)
p2.set_title('sigmoid')
p2.axhline(0.5, ls='--', color='r')
p2.axvline(ls='--', color='r')

p3 = plt.subplot(313)
y = relu(x)
p3.plot(x, y)
p3.set_title('relu')
p3.axvline(ls='--', color='r')

plt.subplots_adjust(hspace=1)
plt.show()

　　其图形解释如下：

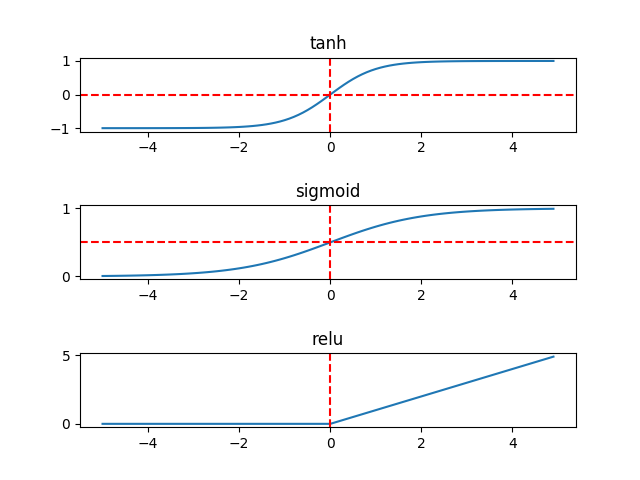
　　相较而言，在隐藏层，tanh函数要优于sigmoid函数，可以认为是sigmoid的平移版本，优势在于其取值范围介于-1 ~ 1之间，数据的平均值为0，而不像sigmoid为0.5，有类似数据中心化的效果。

　　但在输出层，sigmoid也许会优于tanh函数，原因在于你希望输出结果的概率落在0 ~ 1 之间，比如二元分类，sigmoid可作为输出层的激活函数。

　　但实际应用中，特别是深层网络在训练时，tanh和sigmoid会在端值趋于饱和，造成训练速度减慢，故深层网络的激活函数默认大多采用relu函数，浅层网络可以采用sigmoid和tanh函数。

　　另外有必要了解激活函数的求导公式，在反向传播中才知道是如何进行梯度下降。三个函数的求导结果及推理过程如下：

　　1. sigmoid求导函数：

　　其中，sigmoid函数定义为 y = 1/(1 + e^-x)  = (1 + e^-x)^-1

　　与此相关的基础求导公式：(xⁿ)' = n * x^n-1   和  (e^x)^' = e^x

　　应用链式法则，其求导过程为：dy/dx = -1 * (1 + e^-x)^-2 * e^-x * (-1)

　　　　　　　　　　　　　　　　　　  =  e^-x * (1 + e^-x)^-2

　　　　　　　　　　　　　　　　　　  = (1 + e^-x - 1) / (1 + e^-x)²

　　　　　　　　　　　　　　　　　　  = (1 + e^-x)^-1  -  (1 + e^-x)^-2 

　　　　　　　　　　　　　　　　　　  = y - y² 

　　　　　　　　　　　　　　　　　　  = y(1 -y)

2. tanh求导函数：

　　其中，tanh函数定义为 y = (e^x - e^-x)/(e^x + e^-x)

　　与此相关的基础求导公式：(u/v)^' = (u^' v - uv^') / v²

　　同样应用链式法则，其求导过程为：dy/dx = ( (e^x - e^-x)^' * (e^x + e^-x) - (e^x - e^-x) * (e^x + e^-x)^' ) / (e^x + e^-x)²

　　　　　　　　　　　　　　　　　　　　  =  ( (e^x - (-1) * e^-x) * (e^x + e^-x) - (e^x - e^-x) * (e^x + (-1) * e^-x) ) / (e^x + e^-x)² 　　

　　　　　　　　　　　　　　　　　　　　  =  ( (e^x + e^-x)²  -  (e^x - e^-x)² ) / (e^x + e^-x)²

　　　　　　　　　　　　　　　　　　　　  =  1 -  ( (e^x - e^-x)/(e^x + e^-x) )²

　　　　　　　　　　　　　　　　　　　　  = 1 - y²

　　3. relu求导函数：

　　其中，relu函数定义为 y = max(0, x)

　　可以简单推理出 当x <0 时，dy/dx = 0; 当 x >= 0时，dy/dx = 1