【NLP】揭秘马尔可夫模型神秘面纱系列文章(三)
向前算法解决隐马尔可夫模型似然度问题
作者:白宁超
2016年7月11日22:54:57
摘要:最早接触马尔可夫模型的定义源于吴军先生《数学之美》一书,起初觉得深奥难懂且无什么用场。直到学习自然语言处理时,才真正使用到隐马尔可夫模型,并体会到此模型的妙用之处。马尔可夫模型在处理序列分类时具体强大的功能,诸如解决:词类标注、语音识别、句子切分、字素音位转换、局部句法剖析、语块分析、命名实体识别、信息抽取等。另外广泛应用于自然科学、工程技术、生物科技、公用事业、信道编码等多个领域。本文写作思路如下:第一篇对马尔可夫个人简介和马尔科夫链的介绍;第二篇介绍马尔可夫链(显马尔可夫模型)和隐马尔可夫模型以及隐马尔可夫模型的三大问题(似然度、编码、参数学习);第三至五篇逐一介绍三大问题相关算法:(向前算法、维特比算法、向前向后算法);最后非常得益于冯志伟先生自然语言处理教程一书,冯老研究自然语言几十余载,在此领域别有建树。(本文原创,转载注明出处:向前算法解决隐马尔可夫模型似然度问题 )
目录
【自然语言处理:马尔可夫模型(一)】:初识马尔可夫和马尔可夫链
【自然语言处理:马尔可夫模型(二)】:马尔可夫模型与隐马尔可夫模型
【自然语言处理:马尔可夫模型(三)】:向前算法解决隐马尔可夫模型似然度问题
【自然语言处理:马尔可夫模型(四)】:维特比算法解决隐马尔可夫模型解码问题(中文句法标注)
【自然语言处理:马尔可夫模型(五)】:向前向后算法解决隐马尔可夫模型机器学习问题
马尔可夫个人简介
安德烈·马尔可夫,俄罗斯人,物理-数学博士,圣彼得堡科学院院士,彼得堡数学学派的代表人物,以数论和概率论方面的工作著称,他的主要著作有《概率演算》等。1878年,荣获金质奖章,1905年被授予功勋教授称号。马尔可夫是彼得堡数学学派的代表人物。以数论和概率论方面的工作著称。他的主要著作有《概率演算》等。在数论方面,他研究了连分数和二次不定式理论 ,解决了许多难题 。在概率论中,他发展了矩阵法,扩大了大数律和中心极限定理的应用范围。马尔可夫最重要的工作是在1906~1912年间,提出并研究了一种能用数学分析方法研究自然过程的一般图式——马尔可夫链。同时开创了对一种无后效性的随机过程——马尔可夫过程的研究。马尔可夫经多次观察试验发现,一个系统的状态转换过程中第n次转换获得的状态常取决于前一次(第(n-1)次)试验的结果。马尔可夫进行深入研究后指出:对于一个系统,由一个状态转至另一个状态的转换过程中,存在着转移概率,并且这种转移概率可以依据其紧接的前一种状态推算出来,与该系统的原始状态和此次转移前的马尔可夫过程无关。马尔可夫链理论与方法在现代已经被广泛应用于自然科学、工程技术和公用事业中。
1 向前算法原理描述
向前算法解决:问题1(似然度问题):给一个HMM λ=(A,B) 和一个观察序列O,确定观察序列的似然度问题 P=(O|λ) 。
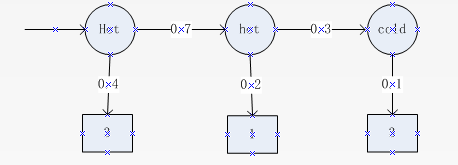
对于马尔可夫链,表面观察和实际隐藏是相同的,只需要标记吃冰淇淋数目“3 1 3”的状态,把加权(弧上)的对应概率相乘即可。而隐马尔可夫模型就不是那么简单了,因为状态是隐藏的,我们并不知道隐藏的状态序列是什么?
简化下问题:假如我们知道天气热冷状况,并且知道小明吃冰淇淋的数量,我们去观察序列似然度。如:对于给定的隐藏状态序列“hot hot cold”我们来计算观察序列“3 1 3”的输出似然度。
如何进行计算?首先,隐马尔可夫模型中,每个隐藏状态只产生一个单独的观察即一一映射,隐藏状态序列与观察序列长度相同,即:给定这种一对一的映射以及马尔可夫假设,对于一个特定隐藏状态序列 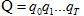 以及一个观察序列
以及一个观察序列 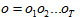 观察序列的似然度为:
观察序列的似然度为:

故从隐藏状态“hot hot cold”到所吃冰淇淋观察序列“3 1 3”的向前概率为:
P(3 1 3|hot hot cold)=P(3|hot)*P(1|hot)*P(3|cold)=0.4*0.2*0.1=0.008
实际上,隐藏状态序列“hot hot cold”是我们的假设,并不知道隐藏状态序列,我们要考虑所有可能的天气序列,如此一来,我们将计算所有可能的联合概率,计算将会变得特别复杂。
我们来计算天气序列Q生产一个特定的冰淇淋事件序列O的联合概率:
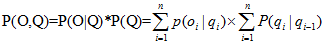
如果隐藏序列只有一个是“hot hot cold”,那么我们的冰淇淋观察“3 1 3”和一个可能的隐藏状态“hot hot cold”的联合概率为:
P(313|hothotcold)=P(hot|start)*P(hot|hot)*P(hot|cold)*P(3|hot)*P(1|hot)*P(3|cold)=0.8*0.7*0.30.4*0.2*0.1=0.001344
P(3 1 3)= P(313| cold cold cold)+ P(313| cold cold hot) + P(313| hot hot cold ) + P(313| cold hot cold) + P(313|hot cold cold) + P(313| hot hot hot) + P(313| hot cold hot) + P(313| cold hot hot)
对于具有N个隐藏状态和T个观察序列,将会有 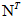 个可能隐藏序列,在实际中T往往很大,比如文本处理中可能有数万几十万个词汇,计算量将是指数上升。在隐含马尔可夫模型中有种向前的算法有效代替这种指数增长的复杂算法,大大降低了复杂度。实验证明向前算法的复杂度是
个可能隐藏序列,在实际中T往往很大,比如文本处理中可能有数万几十万个词汇,计算量将是指数上升。在隐含马尔可夫模型中有种向前的算法有效代替这种指数增长的复杂算法,大大降低了复杂度。实验证明向前算法的复杂度是  。
。
2 向前算法的实例解析
向前算法是一种动态规划算法,当得到观察序列的概率时候,它使用一个表来存储中间值。向前算法也使用对于生成观察序列的所有可能的隐藏状态的路径上的概率求和的方法计算观察概率。在向前算法中横向表示观察序列,纵向表示状态序列。
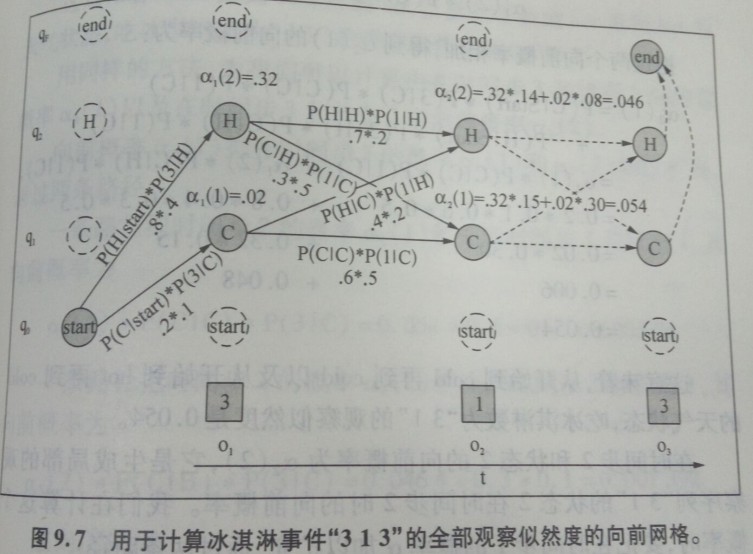
下图是对于给定的隐藏状态序列“hot hot cold”计算观察序列“3 13 ”的似然度的向前网格的例子。其中:
横向:时间上的观察序列,纵向:空间上的状态序列 方框:观察状态 圆框:隐藏状态 续框:不合法转移 实线上值:加权概率
每个单元 表示对于给定的自动机λ,在前面t个观察之后,在状态j的概率:
表示对于给定的自动机λ,在前面t个观察之后,在状态j的概率: 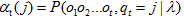 ,其中
,其中  表示第t个状态是状态j的概率。如:
表示第t个状态是状态j的概率。如: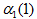 表示状态1即数3时,q1的概率。
表示状态1即数3时,q1的概率。
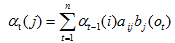
上面公式的3个因素:

向前网格如下:
在时间1和状态1的向前概率:
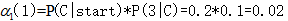
(从状态cold开始吃3根冰淇淋的似然度0.02)
在时间1和状态2的向前概率:
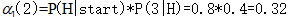
(从状态hot始吃3根冰淇淋的似然度0.32)
在时间2和状态1的向前概率:
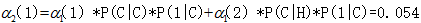
(从开始到cold再到cold以及从开始到hot再到cold的天气状态,吃冰淇淋3 1 的观察似然度0.54)
在时间2和状态2的向前概率:
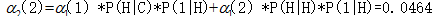
(从开始到cold再到hot以及从开始到hot再到hot的天气状态,吃冰淇淋3 1 的观察似然度0.0464)
用同样方法,我们可以计算时间步3和状态步1的向前概率以及时间步3和状态步2的概率等等,以此类推,直到结束。显而易见,使用向前算法来计算观察似然度可以表示局部观察似然度。这种局部观察似然度比使用联合概率表示的全局观察似然度更有用。
3 向前算法定义
向前算法的递归定义:

4 参考文献
【1】统计自然语言处理基础 Christopher.Manning等 著 宛春法等 译
【2】自然语言处理简明教程 冯志伟 著
【3】数学之美 吴军 著
【4】Viterbi算法分析文章 王亚强
声明:关于此文各个篇章,本人采取梳理扼要,顺畅通明的写作手法。一则参照相关资料二则根据自己理解进行梳理。避免冗杂不清,每篇文章读者可理清核心知识,再找相关文献系统阅读。另外,要学会举一反三,不要死盯着定义或者某个例子不放。诸如:此文章例子冰淇淋数量(观察值)与天气冷热(隐藏值)例子,读者不免问道此有何用?我们将冰淇淋数量换成中文文本或者语音(观察序列),将天气冷热换成英文文本或者语音文字(隐藏序列)。把这个问题解决了不就是解决了文本翻译、语音识别、自然语言理解等等。解决了自然语言的识别和理解,再应用到现在机器人或者其他设备中,不就达到实用和联系现实生活的目的了?本文原创,转载注明出处:向前算法解决隐马尔可夫模型似然度问题
【NLP】揭秘马尔可夫模型神秘面纱系列文章(三)的更多相关文章
- 【NLP】揭秘马尔可夫模型神秘面纱系列文章(一)
初识马尔可夫和马尔可夫链 作者:白宁超 2016年7月10日20:34:20 摘要:最早接触马尔可夫模型的定义源于吴军先生<数学之美>一书,起初觉得深奥难懂且无什么用场.直到学习自然语言处 ...
- 【NLP】揭秘马尔可夫模型神秘面纱系列文章(二)
马尔可夫模型与隐马尔可夫模型 作者:白宁超 2016年7月11日15:31:11 摘要:最早接触马尔可夫模型的定义源于吴军先生<数学之美>一书,起初觉得深奥难懂且无什么用场.直到学习自然语 ...
- 【NLP】揭秘马尔可夫模型神秘面纱系列文章(四)
维特比算法解决隐马尔可夫模型解码问题(中文句法标注) 作者:白宁超 2016年7月12日14:08:28 摘要:最早接触马尔可夫模型的定义源于吴军先生<数学之美>一书,起初觉得深奥难懂且无 ...
- 【NLP】揭秘马尔可夫模型神秘面纱系列文章(五)
向前向后算法解决隐马尔可夫模型机器学习问题 作者:白宁超 2016年7月12日14:28:10 摘要:最早接触马尔可夫模型的定义源于吴军先生<数学之美>一书,起初觉得深奥难懂且无什么用场. ...
- HMM:隐马尔可夫模型HMM
http://blog.csdn.net/pipisorry/article/details/50722178 隐马尔可夫模型 隐马尔可夫模型(Hidden Markov Model,HMM)是统计模 ...
- 隐马尔可夫模型(Hidden Markov Model,HMM)
介绍 崔晓源 翻译 我们通常都习惯寻找一个事物在一段时间里的变化规律.在很多领域我们都希望找到这个规律,比如计算机中的指令顺序,句子中的词顺序和语音中的词顺序等等.一个最适用的例子就是天气的预测. 首 ...
- 隐马尔科夫模型HMM学习最佳范例
谷歌路过这个专门介绍HMM及其相关算法的主页:http://rrurl.cn/vAgKhh 里面图文并茂动感十足,写得通俗易懂,可以说是介绍HMM很好的范例了.一个名为52nlp的博主(google ...
- 用hmmlearn学习隐马尔科夫模型HMM
在之前的HMM系列中,我们对隐马尔科夫模型HMM的原理以及三个问题的求解方法做了总结.本文我们就从实践的角度用Python的hmmlearn库来学习HMM的使用.关于hmmlearn的更多资料在官方文 ...
- 隐马尔可夫模型HMM与维特比Veterbi算法(一)
隐马尔可夫模型HMM与维特比Veterbi算法(一) 主要内容: 1.一个简单的例子 2.生成模式(Generating Patterns) 3.隐藏模式(Hidden Patterns) 4.隐马尔 ...
随机推荐
- ASP.NET MVC with Entity Framework and CSS一书翻译系列文章之第二章:利用模型类创建视图、控制器和数据库
在这一章中,我们将直接进入项目,并且为产品和分类添加一些基本的模型类.我们将在Entity Framework的代码优先模式下,利用这些模型类创建一个数据库.我们还将学习如何在代码中创建数据库上下文类 ...
- CSS float 浮动属性
本篇主要介绍float属性:定义元素朝哪个方向浮动. 目录: 1. 页面布局方式:介绍文档流.浮动层以及float属性. 2. float:left :介绍float为 left 时的布局方式. 3. ...
- Android总结之链式调用(方法链)
前言: 最近在学习总结Android属性动画的时候,发现Android的属性动画设计采用了链式调用的方式,然后又回顾了一下了以前接触的开源框架Glide也是采用链式调用的方式,还有最近火的一塌糊涂的R ...
- Javascript实用方法二
承接上一篇, Object keys object的keys方法能够获取一个给定对象的所有键(key/属性名)并以数组的形式返回.这个方法可以用于键的筛选.匹配等. var basket = { st ...
- [原] KVM 虚拟化原理探究 —— 目录
KVM 虚拟化原理探究 -- 目录 标签(空格分隔): KVM KVM 虚拟化原理探究(1)- overview KVM 虚拟化原理探究(2)- QEMU启动过程 KVM 虚拟化原理探究(3)- CP ...
- HTML+CSS 项目总结
在过去的大概一个月的学习,基本掌握了HTML+CSS的用法和特性. 这个星期老师给我们布置了一个PC端的实战项目,并且要求在3-4天内完成,我不惜废寝忘食,在紧迫的时间内大致地完成了,但是有些效果不能 ...
- JavaScript基础
JavaScript基础 JavaScript是一门编程语言,浏览器内置了JavaScript语言的解释器,所以在浏览器上按照JavaScript语言的规则编写相应代码之,浏览器可以解释并做出相应的处 ...
- 一点公益商城开发系统模式Ring Buffer+
一个队列如果只生产不消费肯定不行的,那么如何及时消费Ring Buffer的数据呢?简单的方案就是当Ring Buffer"写满"的时候一次性将数据"消费"掉. ...
- sublime text 3 + python配置,完整搭建及常用插件安装
四年的时间,一直使用EmEditor编辑器进行Python开发,之前是做面向过程,只需要将一个单独的py文件维护好即可,用着也挺顺手,但是最近在做面向对象的开发,不同的py文件中相互关联较多,感觉单纯 ...
- Aop动态生成代理类时支持带参数构造函数
一.背景 在某些情况下,我们需要植入AOP代码的类并没有默认构造函数.那么此时动态生成的代理类也需要相同签名的构造函数,并且内部调用原始类的构造函数.自己折腾了1晚上没搞定,现在搞定了发出来供大家一起 ...
