PCA(Principal Component Analysis）主成分分析法的数学原理推导
1、主成分分析法PCA的特点与作用如下：
(1)是一种非监督学习的机器学习算法
(2)主要用于数据的降维
(3)通过降维，可以发现人类更加方便理解的特征
(4)其他的应用：去燥；可视化等
2、主成分分析法的数学原理主要是利用梯度上升法来最优化目标函数，即利用梯度上升法来求取效用函数的最大值，其具体的数学原理推导过程如下所示：

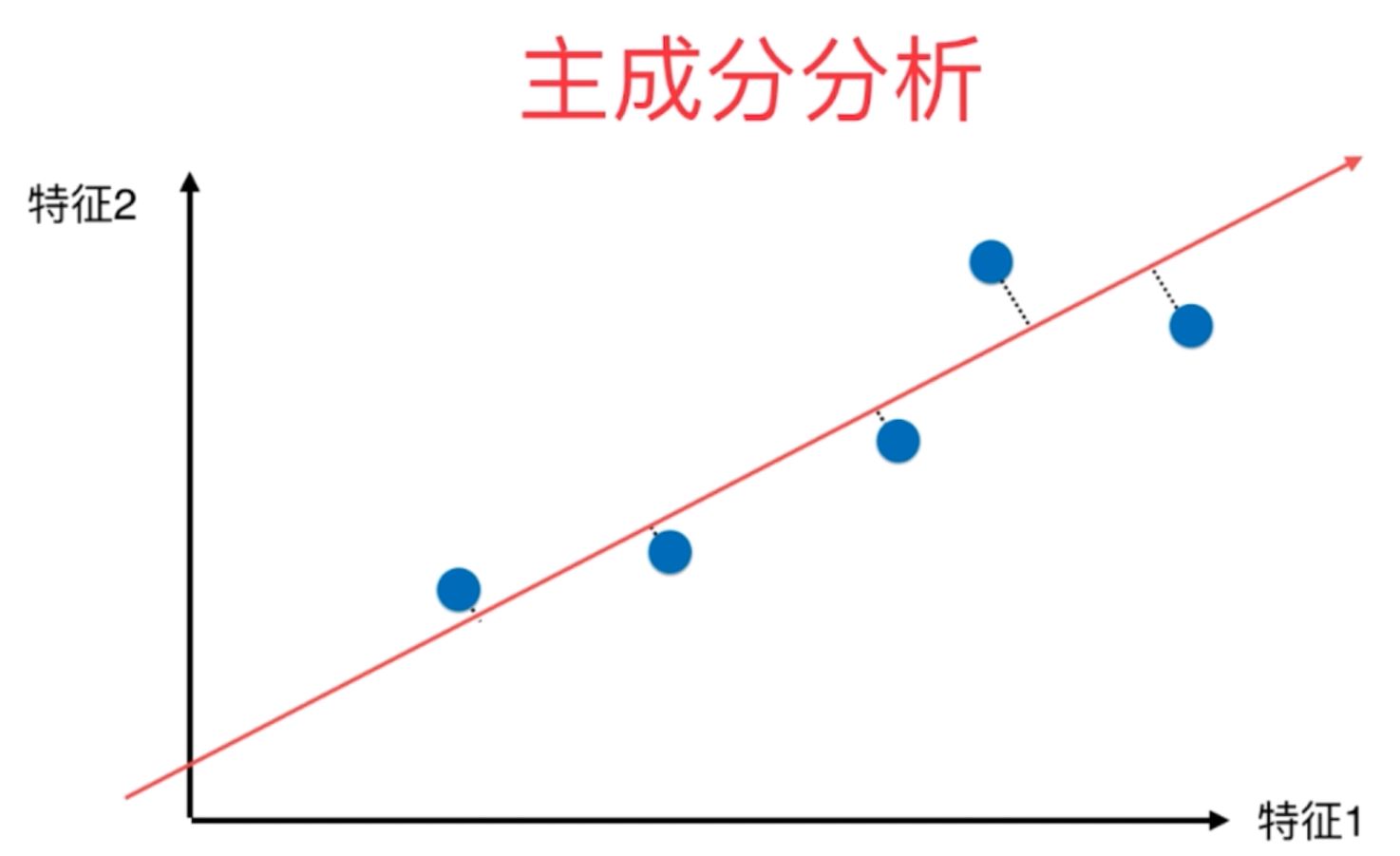
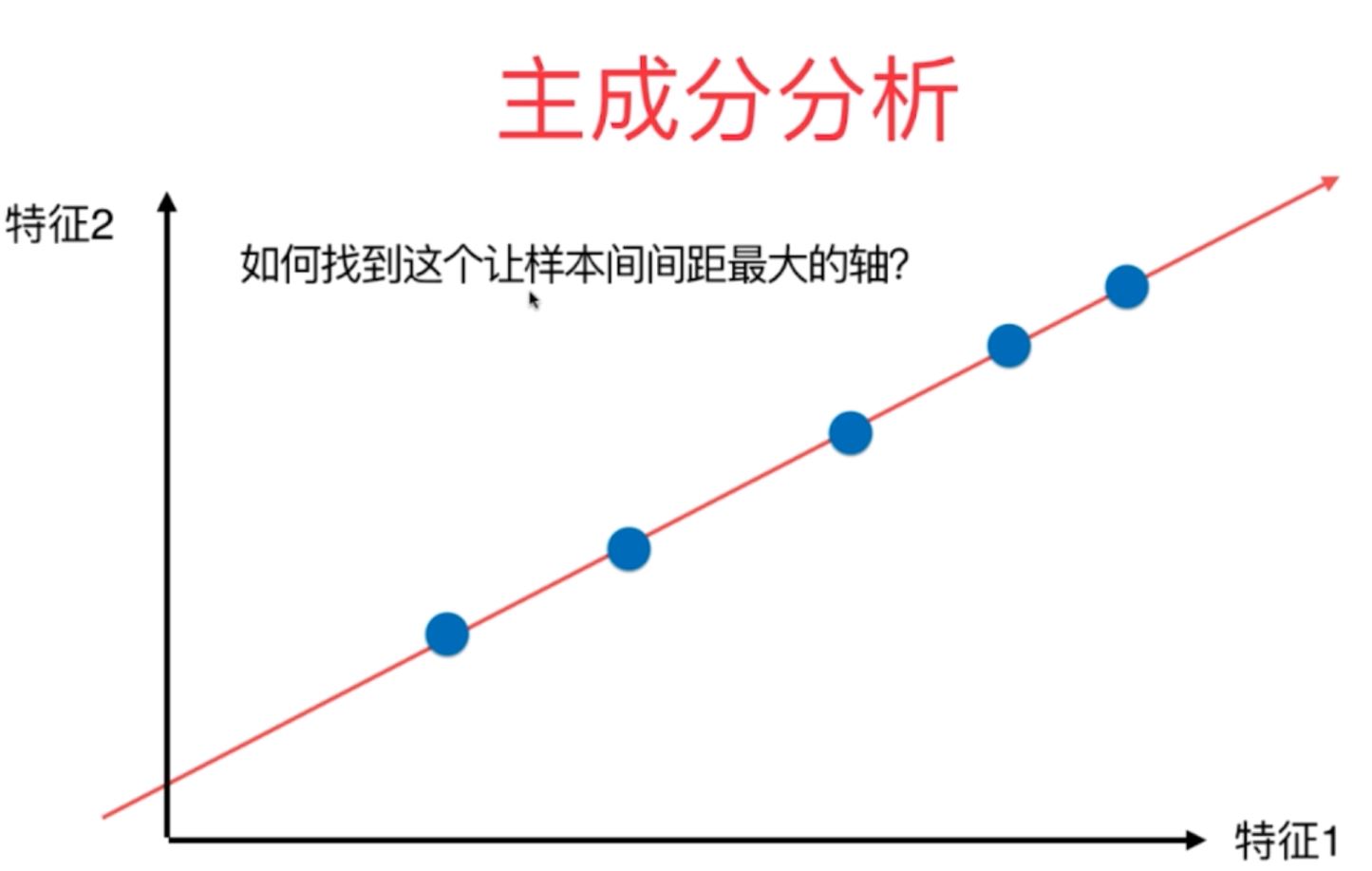
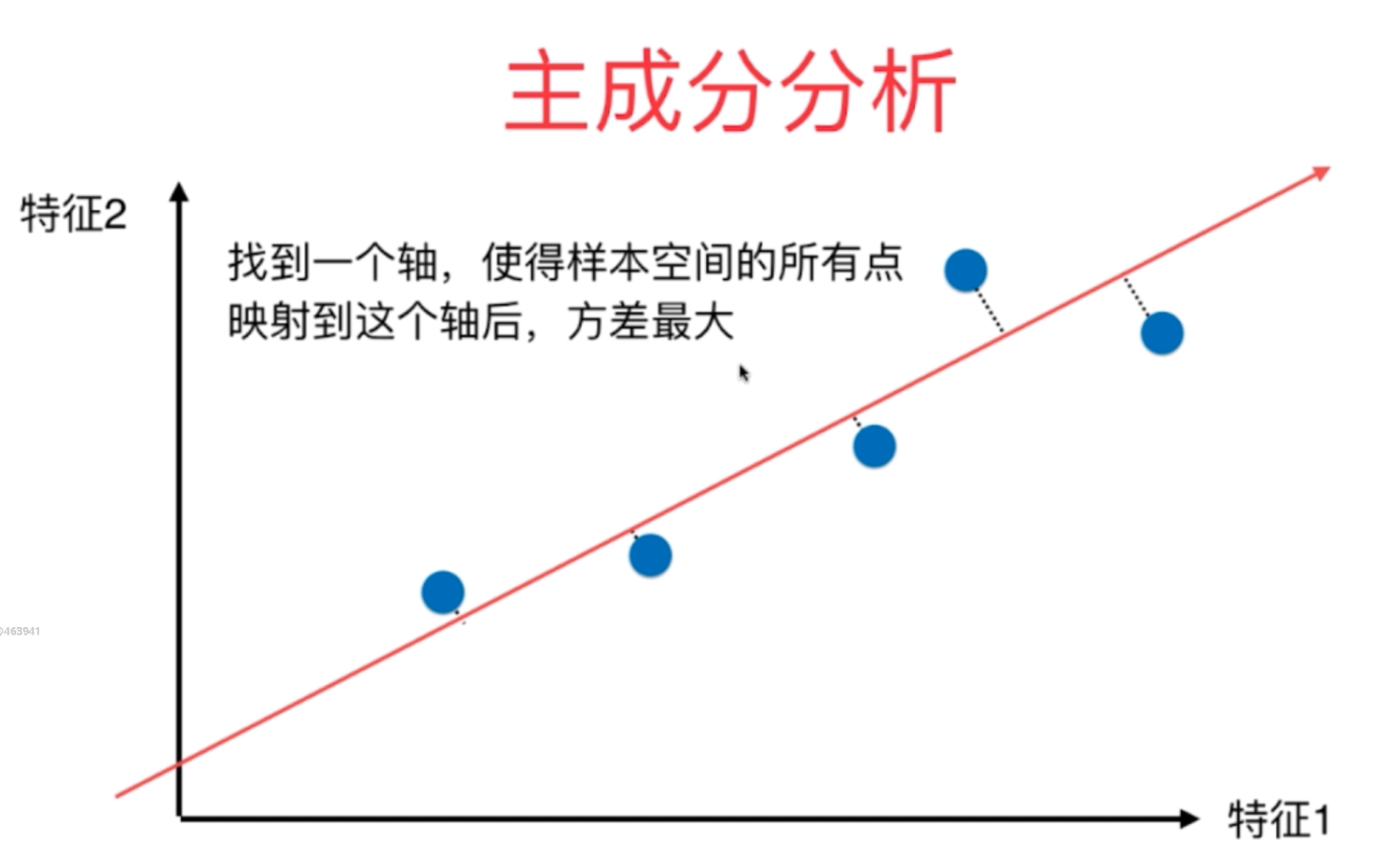
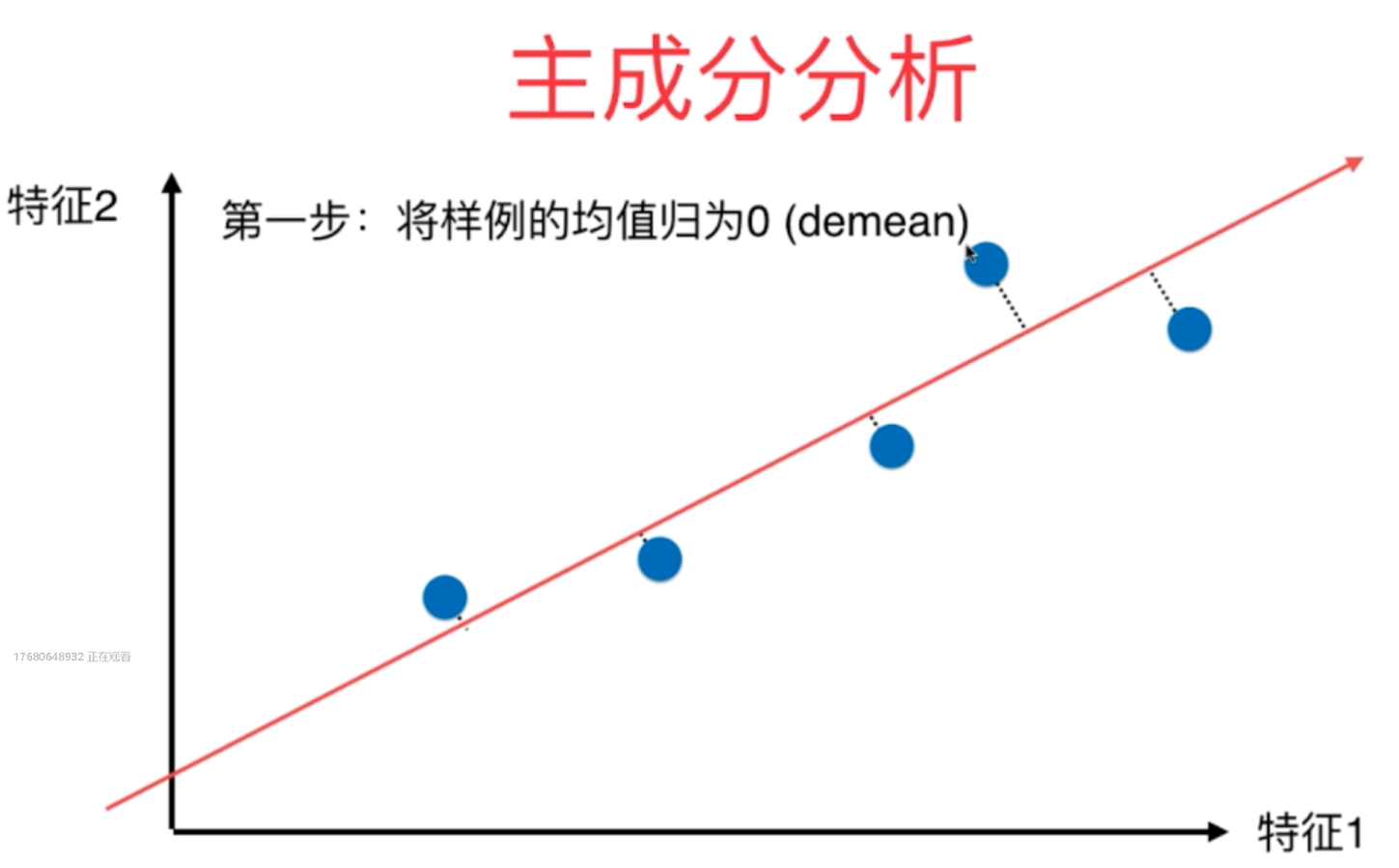
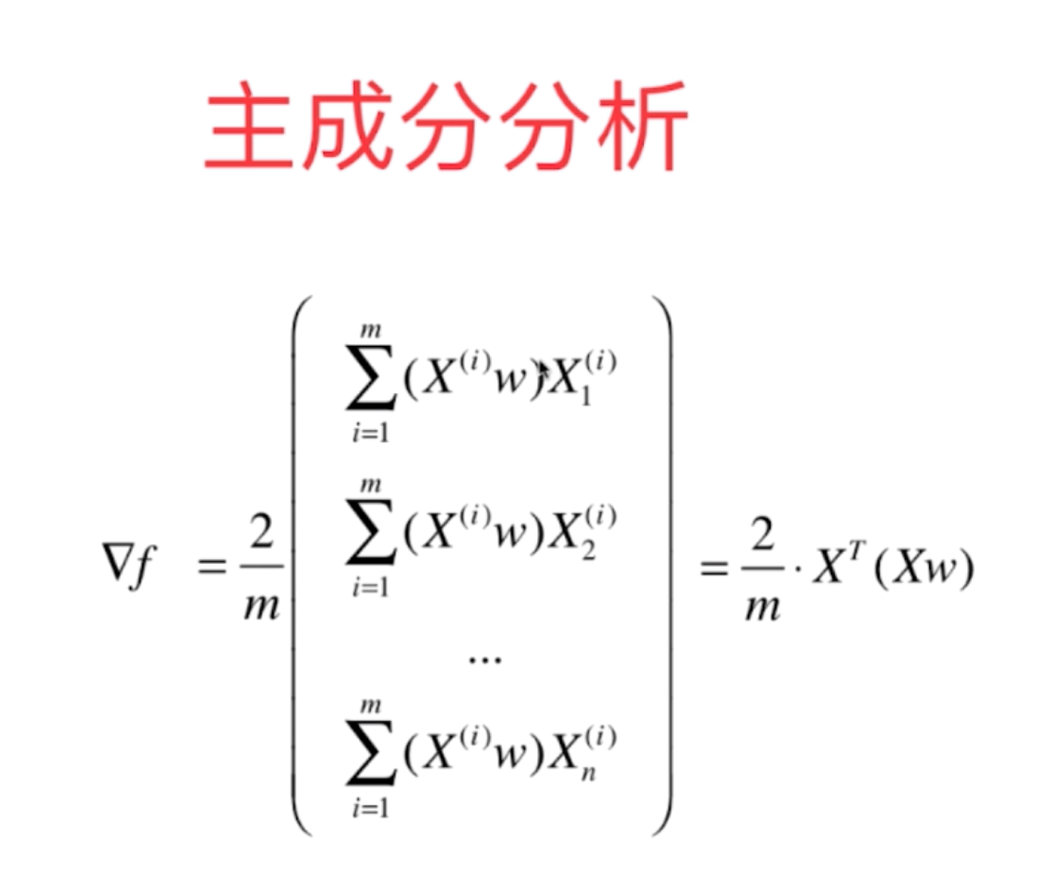
对于以上的函数，因为梯度的向量化表示我们已经求得，因此，我们便可以通过梯度上升法求取函数的最大值！

PCA主成分分析算法的数学原理推导的更多相关文章

  1. 机器学习 - 算法 - Xgboost 数学原理推导

    工作原理 基于集成算法的多个树累加, 可以理解为是弱分类器的提升模型 公式表达 基本公式 目标函数 目标函数这里加入了损失函数计算 这里的公式是用的均方误差方式来计算 最优函数解 要对所有的样本的损失 ...

  2. SVM数学原理推导

    //2019.08.17 #支撑向量机SVM(Support Vector Machine)1.支撑向量机SVM是一种非常重要和广泛的机器学习算法,它的算法出发点是尽可能找到最优的决策边界,使得模型的 ...

  3. opencv——PCA（主要成分分析）数学原理推导

    引言: 最近一直在学习主成分分析(PCA),所以想把最近学的一点知识整理一下,如果有不对的还请大家帮忙指正,共同学习. 首先我们知道当数据维度太大时,我们通常需要进行降维处理,降维处理的方式有很多种, ...

  4. SVM数学原理推导&鸢尾花实例

    //看了多少遍SVM的数学原理讲解,就是不懂,对偶形式推导也是不懂,看来我真的是不太适合学数学啊,这是面试前最后一次认真的看,并且使用了sklearn包中的SVM来进行实现了一个鸢尾花分类的实例,进行 ...

  5. Dijkstar算法的数学原理

    Dijkstar算法是荷兰数学家迪克斯屈拉(or迪杰斯特拉?)在1959年发现的一个算法.是现有的几个求带权图中两个顶点之间最短通路的算法之一.算是一个相当经典的算法了. 迪克斯屈拉算法应用于无向连通 ...

  6. PCA(主成分分析)算法

    设有\(m\)个指标,\(n\)个样本的原始数据 将原始数据按列组成矩阵 \(X _ { n \times m }\) 将\(X\) 的每一列进行中心化 求\(X\)的协方差矩阵\(\Sigma _ ...

  7. [杂记]对RSA算法的数学原理的一点思考

  8. DH算法图解+数学证明

    前几天和同事讨论IKE密钥交换流程时,提到了Diffie-Hellman交换.DH算法最主要的作用便是在不安全的网络上成功公共密钥(并未传输真实密钥).但由于对于DH算法的数学原理则不清楚,因此私下对 ...

  9. 深入学习主成分分析（PCA）算法原理（Python实现）

    一:引入问题 首先看一个表格,下表是某些学生的语文,数学,物理,化学成绩统计: 首先,假设这些科目成绩不相关,也就是说某一科目考多少分与其他科目没有关系,那么如何判断三个学生的优秀程度呢?首先我们一眼 ...

随机推荐

  1. HDU1024 Max Sum Plus Plus （优化线性dp）

    Now I think you have got an AC in Ignatius.L's "Max Sum" problem. To be a brave ACMer, we ...

  2. Python与线性代数——Numpy中的matrix()和array()的区别

    Numpy中matrix必须是2维的,但是 numpy中array可以是多维的(1D,2D,3D····ND).matrix是array的一个小的分支,包含于array.所以matrix 拥有arra ...

  3. 十八、sun JPA理解及使用

    1.JPA理解及实现:    JPA(Java Persistence API)作为Java EE 5.0平台标准的ORM规范,将得到所有Java EE服务器的支持,是SUN在充分吸收现有ORM框架的 ...

  4. iOS 开发之 23种设计模式

    整理了 iOS 开发中用到的设计模式: iOS 开发之 设计模式[一]原型模式 (Prototype pattern) iOS 开发之 设计模式[二]工厂方法模式 iOS 开发之 设计模式[三]抽象工 ...

  5. stm32CubeMx lwip + freeRTOS

    MCU: STM32F429IGT6 工具:STM32CubeMx  版本号 5.0.0 Keil uVersion5 目的:使用LWIP 实现简单的网络连通 一  简介 LWIP(Light Wei ...

  6. Java 笔试题

    有一些还是存在问题,欢迎大家一起探讨. 在Java类中,使用以下( )声明语句来定义公有的int型常量MAX. A. public int MAX = 100; B. final int MAX = ...

  7. Unity3D~纹理格式

    因为之前自己从来没有好好看过这部分,一直都是用的DXT压缩图片,结果发现原来ios是不支持DXT的, 还不知道我项目那么卡是不是这部分引起的, 但愿是~这样应该就可以解决游戏在ios上只有6.8帧的问 ...

  8. Lucene学习笔记一

    Lucene课件 1.全文检索 1.1常见的全文检索 在window系统中,可以指定磁盘中的某一个位置来搜索你想要得到的东西.这个功能是windows比较常用的功能.在这个界面中能搜索的内容有*.*, ...

  9. [转]BeanUtil使用

    BeanUtils的使用 转载自:https://blog.csdn.net/xxf159797/article/details/53645722 1.commons-beanutils的介绍 com ...

  10. 吴裕雄 Bootstrap 前端框架开发——Bootstrap 显示代码：同一行代码片段: span, div

    <!DOCTYPE html> <html> <head> <meta charset="utf-8"> <title> ...