一步一步理解AdaBoosting(Adaptive Boosting)算法

最近学习《西瓜书》的集成学习之Boosting算法，看了一个很好的例子（https://zhuanlan.zhihu.com/p/27126737），为了方便以后理解，现在更详细描述一下步骤。
AdaBoosting(Adaptive Boosting)算法本质思想如下:
以最大准确率拟合第一个学习器；
第二个需要修正第一个的错误：筛选出错误并把它们放大；
第三个再修正之前的错误；
重复以上步骤，直到学习器数目达事先指定的值，再将这些学习器进行加权结合。

给定数据集如下：

注：
1）y的取值只有1和-1，没有其他任何值。

准备工作：
现在我们要选一个threshold值使得这个数据集最后的预测结果误差最小。
比如选threshold =0.5
如果有选择器规则，所有（x>0.5）都被判定为-1，（x<0.5）都被判定为1 。这样明显可以看出x = 1/2/6/7/8都是被预测错误，错误率达到了0.5 。
按照这样的方法，来计算出每个threshold对应的错误是多少，如下图：

再如选threshold =0.5
如果有另一个选择器规则，所有（x<0.5）都被判定为-1，（x>0.5）都被判定为1 。这样明显可以看出x = 0/3/4/5/9都是被预测错误，错误率达到了0.5 。
按照这样的方法，来计算出每个threshold对应的错误是多少，如下图：

了解这些之后，进入第一轮学习器建立过程。

===========================第m=1个学习器学习过程：=================================================================================
第m=1个学习器学习过程：
w是指每个数据的权重，最开始我们没有任何信息的时候默认权重一样，即1/n（n是样本数据个数）。

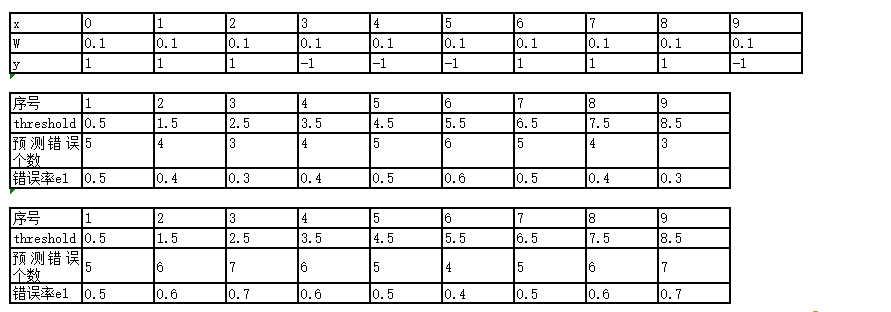
错误率e1:是由相应的权重之和得到的。
找到错误率最小的，显然当Threshold = 2.5时， 此时x= 6/7/8 出错，错误率e1 = 0.1+0.1+0.1（即权重w之和）。
也即学习器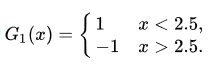
根据e1计算出学习器系数alpha1 = 0.4236。公式为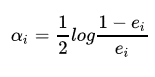
很简单推导可以得出这个式子中，当（ei<1/2），（alphai>0）是有意义的。
根据以下式子开始推导下一轮的数据权重：

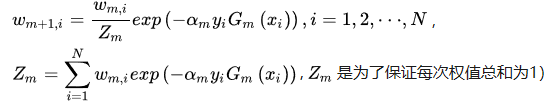
那么我们先算Zm（第一轮学习器的权重跟新总和）：在本轮中有三个数据权重需要增大，剩下七个数据权重减小。
Z1 = 0.13exp(alpha1)+ 0.17exp(0-alpha1) = 3exp( 0.4236 ) +7exp(0 - 0.4236)
W10=W11=W12=W13=W14=W15=W19 = 0.1* 3exp(alpha1)/Z1 = 0.13exp(0.4236)/Z1 = 0.07143
W16=W17=W18 = 0.13exp(0 - alpha1)/Z1 = 0.13*exp(0 - 0.4236)/Z1 = 0.16667
更新后的详细权重如下：

此时更新之后的假设算法和学习器关系为：

根据得到的算法使用最初的数据集发现还是并不能很好地预测出分类，所以还要继续学习过程

===========================第m=2个学习器学习过程：=================================================================================

显然在threshold = 8.5时，错误率最小，可以得到x = 3/4/5的时候出现了错误，错误率e2 = 0.07143+0.07143+0.07143 = 0.21429，alpha2 = 0.6496。
此时学习器为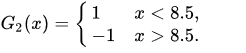
更新权值分布方式如下：
Z2 = 0.0714exp(alpha2 )+0.0714exp(alpha2 )+0.0714exp(alpha2 )+0.0714exp(0 - alpha2 )+
0.0714exp(0 - alpha2 )+0.0714exp(0 - alpha2 )+0.16667exp(alpha2 ) + 0.16667exp(alpha2 )+ 0.16667exp(alpha2 )+0.0714exp(alpha2 )
W20=W21=W22=W29 = 0.0714exp(alpha2 )/Z2 = 0.0455
W23=W24=W25= 0.0714exp(0 - alpha2 )/Z2 = 0.16667
W26=W27=W28 = 0.16667*exp(alpha2 )/Z2 = 0.1060
更新之后的权重如下：

此时更新之后的假设算法和学习器关系为：

注：在（x>8.5）的分段，我认为应该是（0.6496（-1）+0.4236（-1）= --1.0723）但是这里不影响最终的sign[f(x)]结果

根据得到的算法使用最初的数据集发现还是并不能很好地预测出分类，所以还要继续学习过程

===========================第m=3个学习器学习过程：=================================================================================

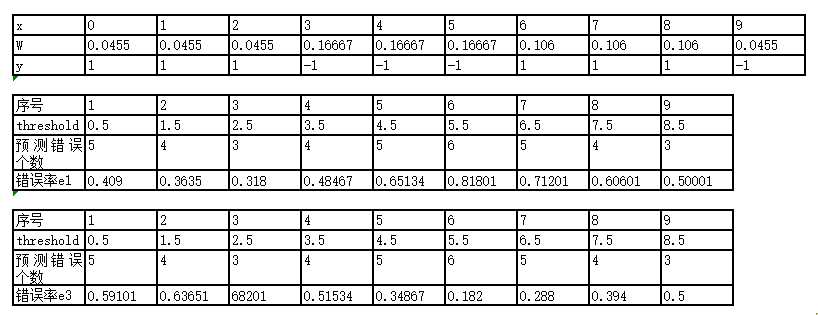
显然在threshold = 5.5时，x =1/2/3/9预测错误 ，错误率最小e3 = 0.182，alpha3 = 0.7514。
此时的学习器为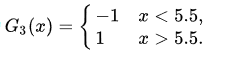
然后来继续更新权值：
Z3=0.0455exp(0 - alpha3 )+0.0455exp(0 - alpha3 )+0.0455exp(0 - alpha3 )+0.16667exp(alpha3 )+0.16667exp(alpha3 )+0.16667exp(alpha3 )+0.1060exp(alpha3 )+0.1060exp(alpha3 )+0.1060exp(alpha3 )+0.0455exp(0 - alpha3 )
W30 = W31=W32= W39 = 0.0455exp(0 - alpha3 )/Z3 = 0.125
W33=W34=W35=0.16667exp(alpha3 )/Z3 = 0.102
W36=W37=W38 = 0.1060*exp(alpha3 )/Z3 = 0.065
更新之后的权重如下：

此时更新之后的假设算法和学习器关系为：

根据得到的算法使用最初的数据集发现可以很好地预测出分类，所以结束学习过程

===========================以上结束=================================================================================
最后扩展内容：
1.Gradient-Boosting
2.在这里我们每个学习器使用的是很简单的sign函数，事实上，更多使用决策树来训练每个基学习器。
3.python实现还没完成