R语言 方差稳定化变换与线性变换 《回归分析与线性统计模型》page96
> rm(list = ls())
> A=read.csv("data96.csv")
> A
Y N
1 11 0.0950
2 7 0.1920
3 7 0.0750
4 19 0.2078
5 9 0.1382
6 4 0.0540
7 3 0.1292
8 1 0.0503
9 3 0.0629
> attach(A) #将数据A的列名直接赋为变量
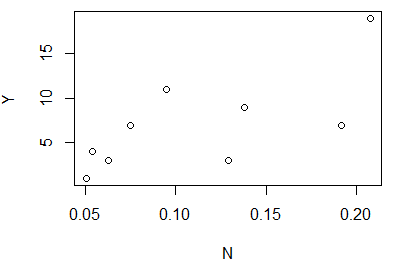
plot(N,Y) #绘制散点图
lm.air=lm(Y~N) #线性回归
summary(lm.air)
e.norm1=(e-mean(e))/sqrt((sum(e^2))/(n-2)) #计算标准化残差 //scale()函数将一组数据进行中心化、标准化 但是我觉得不能用于求标准化残差
plot(Y,e.norm1,ylab = "标准化残差") #绘制标准化残差关于响应变量Y的散点图
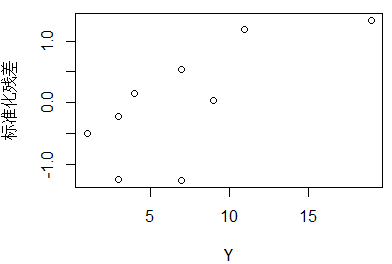
从这个图看出残差随着N的增大而增大,因此似乎违背了方差齐性的假定。因为损害事故数可能是一个泊松分布,其方差与均值成比例。
由于可能是泊松分布,泊松分布的方差与均值有一次比例关系,所以为了保证方差齐性假定,我们做平方根变换。
Z=sqrt(Y)
plot(N,Z) #绘制散点图
lm.air1=lm(Z~N) #线性回归
summary(lm.air1) e1=lm.air1$resid
e.norm1=(e1-mean(e1))/sqrt((sum(e1**2))/(n-2)) #标准化残差 plot(Z,e.norm1,ylab = "标准化残差") #绘制标准化残差关于响应变量sqrt(Y)的散点图
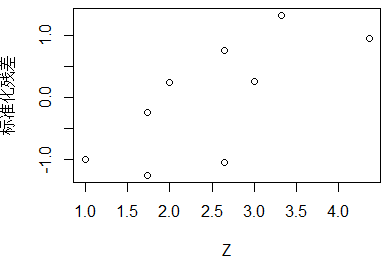
R语言 方差稳定化变换与线性变换 《回归分析与线性统计模型》page96的更多相关文章
- R语言︱非结构化数据处理神器——rlist包
本文作者:任坤,厦门大学王亚南经济研究院金融硕士生,研究兴趣为计算统计和金融量化交易,pipeR,learnR,rlist等项目的作者. 近年来,非关系型数据逐渐获得了更广泛的关注和使用.下面分别列举 ...
- R WLS矫正方差非齐《回归分析与线性统计模型》page115
rm(list = ls()) A = read.csv("data115.csv") fm = lm(y~x1+x2,data = A) coef(fm) A.cooks = c ...
- R语言 线性回归分析实例 《回归分析与线性统计模型》page72
y,X1,X2,X3 分别表示第 t 年各项税收收入(亿元),某国生产总值GDP(亿元),财政支出(亿元)和商品零售价格指数(%). (1) 建立线性模型: ① 自己编写函数: > librar ...
- R box-cox变换 《回归分析与线性统计模型》page100
> rm(list = ls()) > library(openxlsx) > electric= read.xlsx("data101.xlsx",sheet ...
- R 《回归分析与线性统计模型》page119,4.2
rm(list = ls()) library(openxlsx) library(MASS) data = read.xlsx("xiti_4.xlsx",sheet = 2) ...
- R 《回归分析与线性统计模型》page93.6
rm(list = ls()) #数据处理 library(openxlsx) library(car) library(lmtest) data = read.xlsx("xiti4.xl ...
- R 《回归分析与线性统计模型》page121,4.4
rm(list = ls()) A = read.xlsx("xiti_4.xlsx",sheet = 4) names(A) = c("ord"," ...
- R 《回归分析与线性统计模型》page120,4.3
#P120习题4.3 rm(list = ls()) A = read.xlsx("xiti_4.xlsx",sheet = 3) names(A) = c("ord&q ...
- R 对数变换 《回归分析与线性统计模型》page103
BG:在box-cox变换中,当λ = 0时即为对数变换. 当所分析变量的标准差相对于均值而言比较大时,这种变换特别有用.对数据作对数变换常常起到降低数据波动性和减少不对称性的作用..这一变换也能有效 ...
随机推荐
- ECS 系统 Entity-Component-System
已经推出了很久了, 貌似也有一些人开始使用, 我是在看守望先锋的程序设计相关文章的时候看到 ECS 的, 从它的设计逻辑上看, 核心就是 Composition over inheritance (o ...
- Thymeleaf基本知识(推荐)
原文: http://blog.csdn.net/pdw2009/article/details/44700897 Thymeleaf是个XML/XHTML/HTML5模板引擎,可以用于Web与非We ...
- webpack配置文件里loader的执行顺序:从下到上,从右到左; css-loader开启css模块化modules: true,
注释: options:{ importLoaders: 2 } 解决样式文件里使用@import 'xxx.xxx' 的问题 module: { rules: [{ test: /\.scss$/, ...
- Flask - 闪现flash
1. 像snap一样阅后即焚,在服务器端临时存储数据的地方,如显示错误信息.(也可以用session实现) 2. Flash的底层是session做的,所以要secret_key.可以看源码 3. f ...
- 把PHP大牛记下来,方便以后关注
本帖最后由 fish_study 于 2014-12-31 00:18 编辑 五四陈科学院博主54chen(陈臻),哥学社创始人,前人人网分布式存储nuclear研发人员,现关注erlang.hado ...
- 第2章 PLC1200 与HMI (TP900) 组合仿真连接 编写1200程序,编写HMI 仿真过程拍摄视频
博途V13 与 WINCC PROFESSIONAL V13 创建一个PLC工程 和屏幕的 练习. 在做S1200与 HMI的仿真之前 需要设置控制面板 设置PG/PC口 巡视窗口用于看设备的一些属性 ...
- VOC2012数据集提取自己需要的类的图片和对应的xml标签
根据需要修改路径和自己需要的类即可. import os import os.path import shutil fileDir_ann = r'/home/somnus/tttt/VOC2012/ ...
- 树莓派frp添加为服务管理
1.下载frp https://github.com/fatedier/frp/releases 我是1代的B+,下载arm版的,新的可以用arm64的 frp_0.29.0_linux_arm.ta ...
- linux环境下查看tomcat日志
1.先切换到:cd usr/local/tomcat5/logs 2.tail -f catalina.out 3.这样运行时就可以实时查看运行日志 Ctrl+c 是退出tail命令. alt+E+R ...
- 修剪草坪 HYSBZ - 2442
在一年前赢得了小镇的最佳草坪比赛后,FJ变得很懒,再也没有修剪过草坪.现在,新一轮的最佳草坪比赛又开始了,FJ希望能够再次夺冠. 然而,FJ的草坪非常脏乱,因此,FJ只能够让他的奶牛来完成这项工作.F ...
