HDU 1159.Common Subsequence【动态规划DP】

Problem Description

A subsequence of a given sequence is the given sequence with some elements (possible none) left out. Given a sequence X = <x1, x2, …, xm> another sequence Z = <z1, z2, …, zk> is a subsequence of X if there exists a strictly increasing sequence <i1, i2, …, ik> of indices of X such that for all j = 1,2,…,k, xij = zj. For example, Z = <a, b, f, c> is a subsequence of X = <a, b, c, f, b, c> with index sequence <1, 2, 4, 6>. Given two sequences X and Y the problem is to find the length of the maximum-length common subsequence of X and Y.

The program input is from a text file. Each data set in the file contains two strings representing the given sequences. The sequences are separated by any number of white spaces. The input data are correct. For each set of data the program prints on the standard output the length of the maximum-length common subsequence from the beginning of a separate line.

Sample Input

abcfbc abfcab

programming

contest abcd mnp

Sample Output

4 2 0

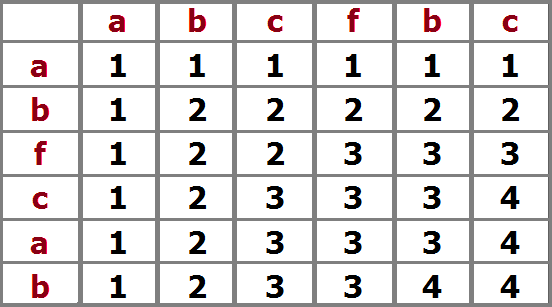
先找第一串第一个字符与第二串的长度， 再找第一串前两个字符与第二串的最长公共子序列长度， 以此类推。 以abcfb 与 abfcab为例，附空间辅助变化示意图，求这两串的最长公共子序列 图中设置的是二维数组，格内的数为行列号，比如，第一个00表示第0行第0列， 由图可以很清晰的看出表达式：F[i][j]=F[i-1][j-1]+1；（a[i]==b[j]）F[i][j]=max(F[i-1][j],F[i][j-1])(a[i]!=b[j]); 当a[i]==b[j]时，长度为 二维数组[i-1][j-1]+1， 不相等时为上格子与前一格子最大值。



代码如下

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int maxn=1000;
int dp[maxn][maxn];
int main()
{
    string x,z;
    int max1,lx,lz;
    while(cin>>x>>z)
    {
        memset(dp,0,sizeof(dp));
        max1=0;
        lx=x.size(),lz=z.size();
        for(int i=1;i<=lx;i++)
        {
            for(int t=1;t<=lz;t++)
            {
                dp[i][t]=max(dp[i][t-1],dp[i-1][t]);
                if(x[i-1]==z[t-1]) dp[i][t]=dp[i-1][t-1]+1;
                if(dp[i][t]>max1) max1=dp[i][t];
            }
        }
        cout<<max1<<endl;
    }
    return 0;
}