2017-ACM南宁网络赛

In this problem, we will define a graph called star graph, and the question is to find the minimum distance between two given nodes in the star graph.

Given an integer nnn, an n−dimensionaln-dimensionaln−dimensional star graph, also referred to as SnS_{n}Sn, is an undirected graph consisting of n!n!n! nodes (or vertices) and ((n−1) ∗ n!)/2((n-1)\ *\ n!)/2((n−1) ∗ n!)/2 edges. Each node is uniquely assigned a label x1 x2 ... xnx_{1}\ x_{2}\ ...\ x_{n}x1 x2 ... xn which is any permutation of the n digits 1,2,3,...,n{1, 2, 3, ..., n}1,2,3,...,n. For instance, an S4S_{4}S4 has the following 24 nodes 1234,1243,1324,1342,1423,1432,2134,2143,2314,2341,2413,2431,3124,3142,3214,3241,3412,3421,4123,4132,4213,4231,4312,4321{1234, 1243, 1324, 1342, 1423, 1432, 2134, 2143, 2314, 2341, 2413, 2431, 3124, 3142, 3214, 3241, 3412, 3421, 4123, 4132, 4213, 4231, 4312, 4321}1234,1243,1324,1342,1423,1432,2134,2143,2314,2341,2413,2431,3124,3142,3214,3241,3412,3421,4123,4132,4213,4231,4312,4321. For each node with label x1 x2x3 x4 ... xnx_{1}\ x_{2} x_{3}\ x_{4}\ ...\ x_{n}x1 x2x3 x4 ... xn, it has n−1n-1n−1 edges connecting to nodes x2 x1 x3 x4 ... xnx_{2}\ x_{1}\ x_{3}\ x_{4}\ ...\ x_{n}x2 x1 x3 x4 ... xn, x3 x2 x1 x4 ... xnx_{3}\ x_{2}\ x_{1}\ x_{4}\ ...\ x_{n}x3 x2 x1 x4 ... xn, x4 x2 x3 x1 ... xnx_{4}\ x_{2}\ x_{3}\ x_{1}\ ...\ x_{n}x4 x2 x3 x1 ... xn, ..., and xn x2 x3 x4 ... x1x_{n}\ x_{2}\ x_{3}\ x_{4}\ ...\ x_{1}xn x2 x3 x4 ... x1. That is, the n−1n-1n−1 adjacent nodes are obtained by swapping the first symbol and the d−thd-thd−th symbol of x1 x2 x3 x4 ... xnx_{1}\ x_{2}\ x_{3}\ x_{4}\ ...\ x_{n}x1 x2 x3 x4 ... xn, for d=2,...,nd = 2, ..., nd=2,...,n. For instance, in S4S_{4}S4, node 123412341234 has 333 edges connecting to nodes 213421342134, 321432143214, and 423142314231. The following figure shows how S4S_{4}S4 looks (note that the symbols aaa, bbb, ccc, and ddd are not nodes; we only use them to show the connectivity between nodes; this is for the clarity of the figure).

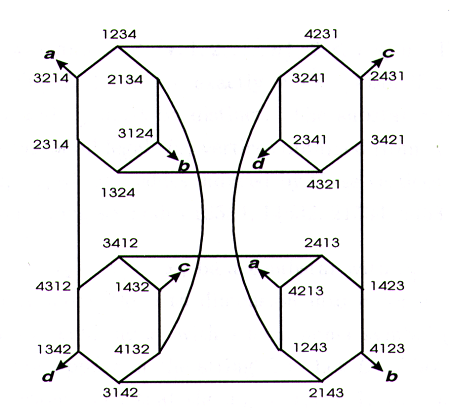
In this problem, you are given the following inputs:

nnn: the dimension of the star graph. We assume that nnn ranges from 444 to 999.
Two nodes x1x_{1}x1 x2x_{2}x2 x3x_{3}x3 ... xnx_{n}xn and y1y_{1}y1 y2y_{2}y2 y3 ... yny_{3}\ ...\ y_{n}y3 ... yn in SnS_{n}Sn.

You have to calculate the distance between these two nodes (which is an integer).

Input Format

nnn (dimension of the star graph)

A list of 555 pairs of nodes.

Output Format

A list of 555 values, each representing the distance of a pair of nodes.

样例输入

样例输出

1

2

2

1

3

vis标记一次就够了

#include<cstdio>

#include<queue>

#include<map>

#include<string>

#include<iostream>

#include<cstring>

#include<algorithm>

using namespace std;

string s,t,v;

int n;

struct node

{

    string s;

    int step;

    node(string str,int n)

    {

        s=str,step=n;

    }

    node()

    {

        s="";

        step=;

    }

};

int bfs()

{

    queue<node>Q;

    map<string,bool>vis;

    Q.push(node(s,));

    vis[s]=;

    while(!Q.empty())

    {

        node u=Q.front();

        Q.pop();

        vis[u.s]=;

        if(u.s==t)  return u.step;

        for(int i=; i<n; ++i)

        {

            v=u.s;

            swap(v[],v[i]);

            if(!vis[v])

            {

                node tc=node(v,u.step+);

                vis[v]=;

                Q.push(tc);

            }

        }

    }

}

int main()

{

    scanf("%d",&n);

    for(int i=; i<=; ++i)

    {

        cin>>s>>t;

        if(s==t)

        {

            puts("");

            continue;

        }

        printf("%d\n",bfs());

    }

}

#include<cstdio>

#include<queue>

#include<map>

#include<string>

#include<iostream>

#include<cstring>

#include<algorithm>

using namespace std;

string s,t,u,v;

int n;

int bfs()

{

    map<string,int>mp;

    queue<string>Q;  //不能用queue<char*>;

    map<string,bool>vis;

    Q.push(s);

    mp[s]=;

    vis[s]=;

    while(!Q.empty())

    {

        u=Q.front();

        Q.pop();

        if(u==t)  return mp[t];

        for(int i=; i<n; ++i)

        {

            v=u;

            swap(v[],v[i]);

            mp[v]=mp[u]+;

            if(!vis[v])

            {

                mp[v]=mp[u]+;

                vis[v]=;

                Q.push(v);

            }

        }

    }

}

int main()

{

    scanf("%d",&n);

    for(int i=; i<=; ++i)

    {

        cin>>s>>t;

        if(s==t)

        {

            puts("");

            continue;

        }

        printf("%d\n",bfs());

    }

}