LU分解法求逆矩阵 C语言实现

最近在网上找了下，没有找到我想要的C语言版本，找到的也是错误的。故自己写了一个，并进行了相关测试，贴出来分享。

具体的LU分解算法就不细说了，随便找本书就知道了，关键是分解的处理流程，细节特别容易出错，一切都在代码里面。

#include <stdio.h>
#include <memory.h>
#include <stdlib.h>

#define N 4
#define DEBUG 1			//debug label，0即不打印相关结果，非0打印相关输出结果

void matrix_inverse_LU(float a[][N])
{
	float l[N][N], u[N][N];
	float l_inverse[N][N], u_inverse[N][N];
	float a_inverse[N][N];
	int i, j, k;
	float s, t;

	memset(l, 0, sizeof(l));
	memset(u, 0, sizeof(u));
	memset(l_inverse, 0, sizeof(l_inverse));
	memset(u_inverse, 0, sizeof(u_inverse));
	memset(a_inverse, 0, sizeof(u_inverse));

	for (i = 0; i < N;i++)		//计算l矩阵对角线
	{
		l[i][i] = 1;
	}

	for (i = 0;i < N;i++)
	{
		for (j = i;j < N;j++)
		{
			s = 0;
			for (k = 0;k < i;k++)
			{
				s += l[i][k] * u[k][j];
			}
			u[i][j] = a[i][j] - s;		//按行计算u值
		}

		for (j = i + 1;j < N;j++)
		{
			s = 0;
			for (k = 0; k < i; k++)
			{
				s += l[j][k] * u[k][i];
			}
			l[j][i] = (a[j][i] - s) / u[i][i];		//按列计算l值
		}
	}

	for (i = 0;i < N;i++)		//按行序，行内从高到低，计算l的逆矩阵
	{
		l_inverse[i][i] = 1;
	}
	for (i= 1;i < N;i++)
	{
		for (j = 0;j < i;j++)
		{
			s = 0;
			for (k = 0;k < i;k++)
			{
				s += l[i][k] * l_inverse[k][j];
			}
			l_inverse[i][j] = -s;
		}
	}

#if DEBUG
	printf("test l_inverse:\n");
	for (i = 0; i < N; i++)
	{
		for (j = 0; j < N; j++)
		{
			s = 0;
			for (k = 0; k < N; k++)
			{
				s += l[i][k] * l_inverse[k][j];
			}

			printf("%f ", s);
		}
		putchar('\n');
	}
#endif

	for (i = 0;i < N;i++)					//按列序，列内按照从下到上，计算u的逆矩阵
	{
		u_inverse[i][i] = 1 / u[i][i];
	}
	for (i = 1;i < N;i++)
	{
		for (j = i - 1;j >=0;j--)
		{
			s = 0;
			for (k = j + 1;k <= i;k++)
			{
				s += u[j][k] * u_inverse[k][i];
			}
			u_inverse[j][i] = -s / u[j][j];
		}
	}

#if DEBUG
	printf("test u_inverse:\n");
	for (i = 0;i < N;i++)
	{
		for (j = 0;j < N;j++)
		{
			s = 0;
			for (k = 0;k < N;k++)
			{
				s += u[i][k] * u_inverse[k][j];
			}

			printf("%f ",s);
		}
		putchar('\n');
	}
#endif

	for (i = 0;i < N;i++)			//计算矩阵a的逆矩阵
	{
		for (j = 0;j < N;j++)
		{
			for (k = 0;k < N;k++)
			{
				a_inverse[i][j] += u_inverse[i][k] * l_inverse[k][j];
			}
		}
	}

#if DEBUG
	printf("test a:\n");
	for (i = 0; i < N; i++)
	{
		for (j = 0; j < N; j++)
		{
			s = 0;
			for (k = 0; k < N; k++)
			{
				s += a[i][k] * a_inverse[k][j];
			}

			printf("%f ", s);
		}
		putchar('\n');
	}
#endif
}

void main()
{
	int i, j, k;
	float a[N][N];

	for (i = 0;i < N;i++)
	{
		for (j = 0;j < N;j++)
		{
			a[i][j] = rand() % 10;
		}
	}

	matrix_inverse_LU(a);
}

　　提醒一下，打印出来的验证结果，可能跟单位矩阵E有稍许不同，如下图所示：

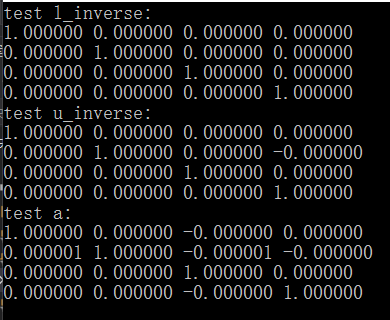
主要是因为相关浮点数计算误差所致，系统原因，不是算法问题。

解决这个问题的方法，就是用更精确的double类型或者改用各适合进行科学计算的工具/语言。