【洛谷P1983 车站分级】

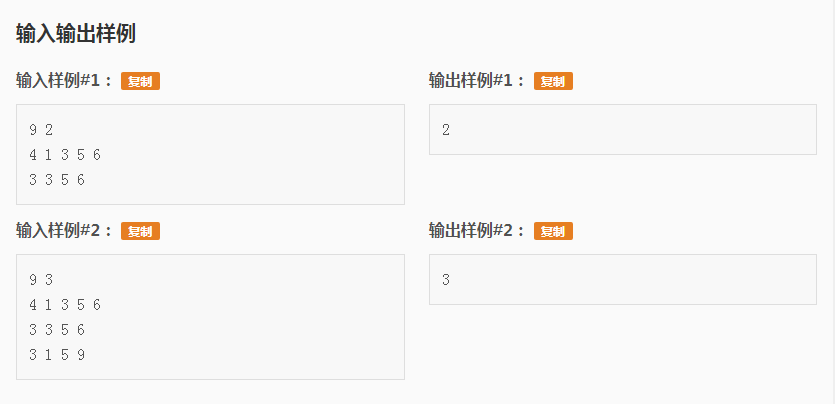
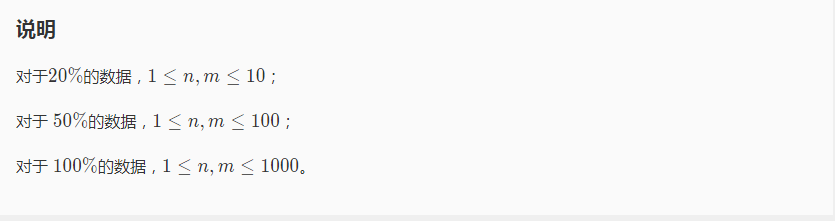
这题好像是个蓝题。（不过也确实差不多QwQ）用到了拓扑排序的知识

我们看这些这车站，沿途停过的车站一定比未停的车站的级别高

所以，未停靠的车站向已经停靠的车站连一条边，入度为0的车站级别就看做1

然后我们把入度为0的边依次取出来，那么它的出边所指车站就一定比这个车站级别高

那么也就是说，一个车站的级别一定比所有指向它的车站中，级别最高的那个车站级别还要高1级

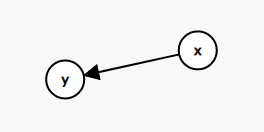（x的级别小于y）

再跑一个拓扑就行了qwq

Code：

#include<bits/stdc++.h>
using namespace std;
const int maxm=;
const int maxn=;
int head[maxm],to[maxm],nxt[maxm];
int in[maxn],cnt,dep[maxn];
int a[maxn],flag[maxn],vis[maxn][maxn],ans;
inline void add(int u,int v)
{
    cnt++;
    to[cnt]=v;
    nxt[cnt]=head[u];
    head[u]=cnt;
}
int n,m;
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=;i<=m;i++)
    {
        memset(a,,sizeof(a));
        memset(flag,,sizeof(flag));
        int k;
        scanf("%d",&k);
        for(int j=;j<=k;j++)
        {
            scanf("%d",&a[j]);
            flag[a[j]]=;
        }
        for(int j=a[]+;j<=a[k];j++)
        {
            if(!flag[j])
            {
                for(int p=;p<=k;p++)
                {
                    if(!vis[j][a[p]])
                    {
                        in[a[p]]++;
                        add(j,a[p]);
                        vis[j][a[p]]=;
                    }
                }
            }
        }
    }
    queue<int> q;
    for(int i=;i<=n;i++)
    {
        if(!in[i])
        {
            q.push(i);
            dep[i]=;
        }
    }
    while(!q.empty())
    {
        int top=q.front();
        q.pop();
        for(int e=head[top];e;e=nxt[e])
        {
            int v=to[e];
            dep[v]=max(dep[v],dep[top]+);
            ans=max(ans,dep[v]);
            in[to[e]]--;
            if(!in[to[e]])
            {
                q.push(to[e]);
            }
        }
    }
    cout<<ans;
    return ;
}