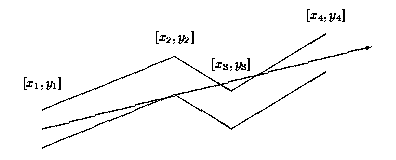
[ACM_几何] Pipe

http://acm.hust.edu.cn/vjudge/contest/view.action?cid=28417#problem/B

 

  本题大意: 给定一个管道上边界的拐点，管道宽为1，求一束光最远能照到的地方的X坐标，如果能照到终点，则输出...

  解题思路: 若想照的最远，则光线必过某两个拐点，因此用二分法对所有拐点对进行枚举，找出最远大值即可。

#include<iostream>
#include<cmath>
#include<string.h>
#include<string>
#include<cstdio>
#include<algorithm>
#include<iomanip>

using namespace std;
#define eps 1e-8
#define PI acos(-1.0)

//点和向量
struct Point{
    double x,y;
    Point(double x=,double y=):x(x),y(y){}
    void out(){cout<<"("<<x<<','<<y<<") ";}
};
typedef Point Vector;
Vector operator+(Vector a,Vector b){return Vector(a.x+b.x,a.y+b.y);}
Vector operator-(Vector a,Vector b){return Vector(a.x-b.x,a.y-b.y);}
Vector operator*(Vector a,double p){return Vector(a.x*p,a.y*p);}
Vector operator/(Vector a,double p){return Vector(a.x/p,a.y/p);}
bool operator<(const Vector& a,const Vector& b){return a.x<b.x||(a.x==b.x && a.y<b.y);}
int dcmp(double x){
    if(fabs(x)<eps)return ;
    else return x< ? -:;
}
bool operator==(const Point& a,const Point& b){
    return dcmp(a.x-b.x)== && dcmp(a.y-b.y)==;
}
double Dot(Vector A,Vector B){return A.x*B.x+A.y*B.y;}//向量点积
double Length(Vector A){return sqrt(Dot(A,A));}//向量模长
double Angle(Vector A,Vector B){return acos(Dot(A,B)/Length(A)/Length(B));}//向量夹角
double Cross(Vector A,Vector B){return A.x*B.y-A.y*B.x;}
double Area2(Point A,Point B,Point C){return Cross(B-A,C-A);}//三角形面积的2倍
//绕起点逆时针旋转rad度
Vector Rotate(Vector A,double rad){
    return Vector(A.x*cos(rad)-A.y*sin(rad),A.x*sin(rad)+A.y*cos(rad));
}
double torad(double jiao){return jiao/*PI;}//角度转弧度
double tojiao(double ang){return ang/PI*;}//弧度转角度
//单位法向量
Vector Normal(Vector A){
    double L=Length(A);
    return Vector(-A.y/L,A.x/L);
}
//点和直线
struct Line{
    Point P;//直线上任意一点
    Vector v;//方向向量，他的左边对应的就是半平面
    double ang;//极角，即从x正半轴旋转到向量v所需的角（弧度）
    Line(){}
    Line(Point p,Vector v):P(p),v(v){ang=atan2(v.y,v.x);}
    bool operator<(const Line& L)const {
        return ang<L.ang;
    }
};
//计算直线P+tv和Q+tw的交点（计算前必须确保有唯一交点）即：Cross(v,w)非0
Point GetLineIntersection(Point P,Vector v,Point Q,Vector w){
    Vector u=P-Q;
    double t=Cross(w,u)/Cross(v,w);
    return P+v*t;
}
double getx(Point p1,Point p2,Point p3,Point p4)//找到直线和线段相交的横坐标(求两直线交点）
 {
     double k1=(p2.y-p1.y)/(p2.x-p1.x);
     double k2=(p4.y-p3.y)/(p4.x-p3.x);
     double b1=p2.y-k1*p2.x;
     double b2=p3.y-k2*p3.x;
     return (b2-b1)/(k1-k2);
 }
//点到直线距离(dis between point P and line AB)
double DistanceToLine(Point P,Point A,Point B){
    Vector v1=B-A , v2=P-A;
    return fabs(Cross(v1,v2))/Length(v1);
}
//dis between point P and segment AB
double DistancetoSegment(Point P,Point A,Point B){
    if(A==B)return Length(P-A);
    Vector v1=B-A,v2=P-A,v3=P-B;
    if(dcmp(Dot(v1,v2))<)return  Length(v2);
    else if(dcmp(Dot(v1,v3))>)return Length(v3);
    else return fabs(Cross(v1,v2))/Length(v1);
}
//point P on line AB 投影点
Point GetLineProjection(Point P,Point A,Point B){
    Vector v=B-A;
    return A+v*(Dot(v,P-A)/Dot(v,v));
}
//线段规范相交（只有一个且不在端点）每条线段两端都在另一条两侧，（叉积符号不同）
bool SegmentProperIntersection(Point a1,Point a2,Point b1,Point b2){
    a2=(a2-a1)*+a1;//射线A1A2相交线短B1B2
    double c1=Cross(a2-a1,b1-a1),c2=Cross(a2-a1,b2-a1),
           c3=Cross(b2-b1,a1-b1),c4=Cross(b2-b1,a2-b1);
    return dcmp(c1)*dcmp(c2)< && dcmp(c3)*dcmp(c4)<;
}
//判断点P是否在线段AB上
bool OnSegment(Point p,Point a1,Point a2){
    return dcmp(Cross(a1-p,a2-p))== && dcmp(Dot(a1-p,a2-p))<;
}
//多边形的面积（可以是非凸多边形）
double PolygonArea(Point* p,int n){
    double area=;
    for(int i=;i<n-;i++)
        area+=Cross(p[i]-p[],p[i+]-p[]);
    return area/;
}

//点p在有向直线左边，上面不算
bool OnLeft(Line L,Point p){
    return Cross(L.v,p-L.P)>;
}

double ok(double x,double y,double d,double z){
    double f=fabs(d*(/tan(acos(z/y))+/tan(acos(z/x))))-z;
    if(fabs(f)<1e-)return  ;
    else return f;
}
//计算凸包输入点数组p，个数n，输出点数组ch，返回凸包定点数
//输入不能有重复，完成后输入点顺序被破坏
//如果不希望凸包的边上有输入点，把两个<=改成<
//精度要求高时，建议用dcmp比较
//基于水平的Andrew算法-->1、点排序2、删除重复的然后把前两个放进凸包
//3、从第三个往后当新点在凸包前进左边时继续，否则一次删除最近加入的点，直到新点在左边
int ConVexHull(Point* p,int n,Point*ch){
    sort(p,p+n);
    int m=;
    for(int i=;i<n;i++){//下凸包
        while(m> && Cross(ch[m-]-ch[m-],p[i]-ch[m-])<=)m--;
        ch[m++]=p[i];
    }
    int k=m;
    for(int i=n-;i>=;i--){//上凸包
        while(m>k && Cross(ch[m-]-ch[m-],p[i]-ch[m-])<=)m--;
        ch[m++]=p[i];
    }
    if(n>)m--;
    return m;
}

//******************************************************************************
#define N 21
#define left -10e8
Point up[N],down[N];
int n;

double getans()//最值一定过两个顶点一上一下，所以枚举所有点对
 {
     int i,j,k;
     double ans=left,right;//二分法
     double tx,ty;
     Point ql,qr;
     for(i=;i<n;i++)
     for(j=;j<n;j++)
     {
         if(i==j)continue;
         ql=up[i];
         qr=down[j];
         right=left;//left是左边界，非常小的一个值，right就是枚举的过两点的直线最远能达的x的大小
         for(k=;k<n;k++)//验证枚举直线是否满足所有点
         {
             tx=up[k].x;
             ty=(tx-ql.x)*(qr.y-ql.y)/(qr.x-ql.x)+ql.y;//求出对应x点在枚举的直线上的y值
             if(ty>down[k].y&&ty<up[k].y||fabs(ty-down[k].y)<eps||fabs(ty-up[k].y)<eps)//该y值应在上下之间或与上或下重合
             right=tx;//更新有边界值
             else//如果该点时不满足
             {
                 if(k)//细节！！！
                 {
                     if(ty<down[k].y)
                     right=getx(ql,qr,down[k-],down[k]);
                     else
                     right=getx(ql,qr,up[k-],up[k]);
                 }
                 break;
             }
         }
         if(right>ans)
             ans=right;
     }
     return ans;
 }

int main(){
    cout.precision();
    for(;cin>>n&&n;){
        for(int i=;i<n;i++){
            cin>>up[i].x>>up[i].y;
            down[i].x=up[i].x;
            down[i].y=up[i].y-;
        }
        double ans=getans();
        if(ans>up[n-].x||fabs(ans-up[n-].x)<eps)
        cout<<"Through all the pipe.\n";
        else cout<<fixed<<ans<<'\n';
    }return ;
}