[NOIP2015] 斗地主（搜索）

题目描述

牛牛最近迷上了一种叫斗地主的扑克游戏。斗地主是一种使用黑桃、红心、梅花、方片的A到K加上大小王的共54张牌来进行的扑克牌游戏。在斗地主中，牌的大小关系根据牌的数码表示如下：3<4<5<6<7<8<9<10<J<Q<K<A<2<小王<大王，而花色并不对牌的大小产生影响。每一局游戏中，一副手牌由n张牌组成。游戏者每次可以根据规定的牌型进行出牌，首先打光自己的手牌一方取得游戏的胜利。

现在，牛牛只想知道，对于自己的若干组手牌，分别最少需要多少次出牌可以将它们打光。请你帮他解决这个问题。

需要注意的是，本题中游戏者每次可以出手的牌型与一般的斗地主相似而略有不同。

具体规则如下：

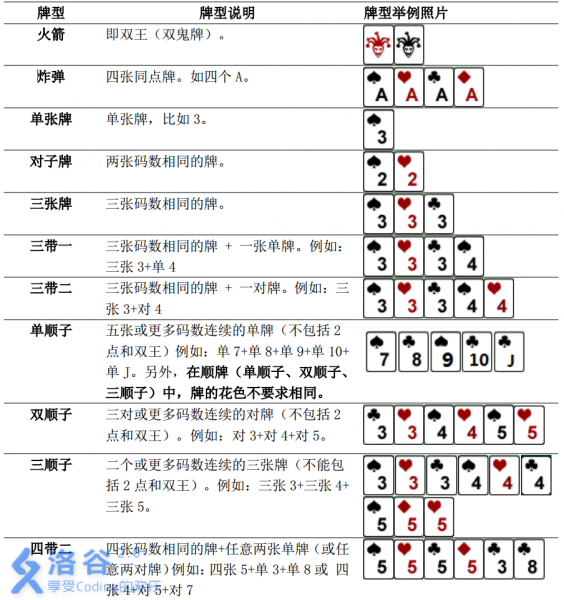
输入输出格式

输入格式：

第一行包含用空格隔开的2个正整数Tn，表示手牌的组数以及每组手牌的张数。

接下来T组数据，每组数据n行，每行一个非负整数对aibi表示一张牌，其中ai示牌的数码，bi表示牌的花色，中间用空格隔开。特别的，我们用1来表示数码A，11表示数码J，12表示数码Q，13表示数码K；黑桃、红心、梅花、方片分别用1-4来表示；小王的表示方法为01，大王的表示方法为02。

输出格式：

共T行，每行一个整数，表示打光第i手牌的最少次数。

输入输出样例

输入样例#1：

1 8
7 4
8 4
9 1
10 4
11 1
5 1
1 4
1 1

输出样例#1：

3

输入样例#2：

1 17
12 3
4 3
2 3
5 4
10 2
3 3
12 2
0 1
1 3
10 1
6 2
12 1
11 3
5 2
12 4
2 2
7 2

输出样例#2：

6

说明

样例1说明

共有1组手牌，包含8张牌：方片7，方片8，黑桃9，方片10，黑桃J，黑桃5，方片A以及黑桃A。可以通过打单顺子（方片7，方片8，黑桃9，方片10，黑桃J），单张牌（黑桃5）以及对子牌（黑桃A以及方片A）在3次内打光。

对于不同的测试点， 我们约定手牌组数T与张数n的规模如下：

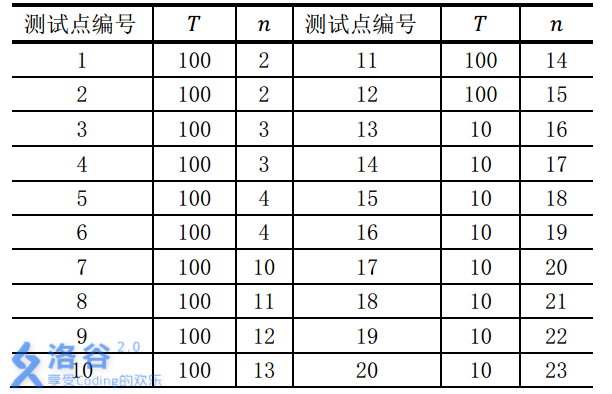
数据保证：所有的手牌都是随机生成的。

• 看道题目我只能说出题人真会玩，斗地主都出来了。
• 这个斗地主的规则与一般的不太一样（虽然是从百度百科上粘的）。
• 看到随机数据我就松了一口气，因为这样的话不会有出题人给的神坑！！！
• 仔细分析，其实这道题没有什么完美的算法，基本确定思路：爆搜（深度优先搜索）。
• 本题花色没什么卵用，只是用来区分大小王。
• 再分析：出牌顺序不会影响出牌次数。
• 按照常规的思路，肯定要先打顺子。
• 所以就先搜顺子；注意：连着的几张牌不一定当做一个顺子一起打出，比如说6 7 8 8 9 9 10 10 J Q这组牌，如果先打出678910JQ，再打3个单牌，就不如打两个顺子678910 8910JQ更优。
• 然后出带牌，也要按照一定的顺序，比如：四带两对，四带两单，三带。
• 然后把所有不能连着出的牌统计一下，加到当前的答案中，并更新答案。
• 注意本题搜索技巧：每次进入下一步是统计一下当前牌号的种类数（因为同一号的牌一定能一下打出），并更新答案；因为A能连成顺子而2不能，所以在将牌编号时可以将3-K编号为1-11，A编号为12，2编号为13，小王为14，大王为15，这样搜的时候就会比较方便；如果有双王先打出双王，因为这样对牌局没有影响（双王不能被同时带出，但单个王可以被带出）；注意利用前缀和的思想，这样可以使搜索更方便（尤其是搜顺子的时候）。
• 然后就是考验代码能力的时候了，本人蒟蒻，调了半天才调出来，代码很丑。
• 复杂度玄学，不过对于随机数据来说不成问题，期望通过本题，最慢的点300+ms。

 var
     t,n,i,j,x,y,anss,tt,now,ans        :longint;
     sum                             :Array[..] of longint;
     f1,f2,f3,s1,s2,s3                :array[..] of longint;
     ff                                :boolean;

 function min(x,y:longint):longint;
 begin
     if x<y then exit(x) else exit(y);
 end;

 function find():longint;
 var
     i,summ                             :longint;
 begin
     summ:=;
     for i:= to  do if (sum[i]>) then inc(summ);
     exit(summ);
 end;

 procedure dfs(x:longint);
 var
     i,j,k                             :longint;
     l,r,max,t,q,o                    :longint;
 begin
     q:=find();
     if q+x-<anss then anss:=q+x-;//tongji
     {---------------------------------------------------}
     fillchar(f1,sizeof(f1),);
     fillchar(s1,sizeof(s1),);
     for i:= to  do if (sum[i]>=) then f1[i]:=;
     for i:= to  do s1[i]:=s1[i-]+f1[i];
     max:=;
     for i:= to  do
     for j:=i+ to  do
         if j<=l then continue;
         if (s1[j]-s1[i-]=j-i+) then
         begin
             if (j-i+>max) then
             begin
                 max:=j-i+;
                 l:=i;
                 r:=j;
             end;
         end;
     if max>= then
     begin
         for i:=l to r do
         for j:=r downto l do
         begin
             if j-i+< then continue;
             for k:=i to j do dec(sum[k],);
             dfs(x+);
             for k:=i to j do inc(sum[k],);
         end;
     end;//san shun zi
     {----------------------------------------------------------}
     fillchar(f2,sizeof(f2),);
     fillchar(s2,sizeof(s2),);
     for i:= to  do if (sum[i]>=) then f2[i]:=;
     for i:= to  do s2[i]:=s2[i-]+f2[i];
     max:=;
     for i:= to  do
     for j:=i+ to  do
         if (s2[j]-s2[i-]=j-i+) then
         begin
             if (j-i+>max) then
             begin
                 max:=j-i+;
                 l:=i;
                 r:=j;
             end;
         end;
     if max>= then
     begin
         for i:=l to r do
         for j:=r downto l do
         begin
             if j-i+< then continue;
             for k:=i to j do dec(sum[k],);
             dfs(x+);
             for k:=i to j do inc(sum[k],);
         end;
     end;//shuang shun zi
     {--------------------------------------------------------}
     fillchar(f3,sizeof(f3),);
     fillchar(s3,sizeof(s3),);
     for i:= to  do if (sum[i]<>) then f3[i]:=;
     for i:= to  do s3[i]:=s3[i-]+f3[i];
     max:=;
     for i:= to  do
     for j:=i+ to  do
         if (s3[j]-s3[i-]=j-i+) then
         begin
             if (j-i+>max) then
             begin
                 max:=j-i+;
                 l:=i;
                 r:=j;
             end;
         end;
     if max>= then
     begin
         for i:=l to r do
         for j:=r downto l do
         begin
             if j-i+< then continue;
             for k:=i to j do dec(sum[k]);
             dfs(x+);
             for k:=i to j do inc(sum[k]);
         end;
     end;//dan shun zi
     {--------------------------------------------------------}
     for i:= to  do
     begin
         if (sum[i]=) then
         begin
             dec(sum[i],);
             for j:= to  do
             begin
                 if sum[j]< then continue;
                 for k:=j+ to  do
                 begin
                     if sum[k]< then continue;
                     dec(sum[j],);
                     dec(sum[k],);
                     dfs(x+);
                     inc(sum[j],);
                     inc(sum[k],);
                 end;
             end;
             inc(sum[i],);
         end;
     end; //4 dai 2
     {-------------------------------------------------------}
     for i:= to  do
     begin
         if (sum[i]=) then
         begin
             dec(sum[i],);
             for j:= to  do
             begin
                 if sum[j]<> then continue;
                 for k:=j+ to  do
                 begin
                     if sum[k]<> then continue;
                     dec(sum[j]);
                     dec(sum[k]);
                     dfs(x+);
                     inc(sum[j]);
                     inc(sum[k]);
                 end;
             end;
             inc(sum[i],);
         end;
     end; //4 dai 1
     {---------------------------------------------------------}
     for i:= to  do
     begin
         if (sum[i]=) then
         begin
             dec(sum[i],);
             for j:= to  do
             begin
                 if (sum[j]>) or (sum[j]<) then continue;
                 t:=sum[j];
                 sum[j]:=;
                 dfs(x+);
                 sum[j]:=t;
             end;
             inc(sum[i],);
         end;
     end;//san dai 1/2
 end;

 begin
     read(t,n);
     while (t>) do
     begin
         dec(t);
         fillchar(sum,sizeof(sum),);
         for i:= to n do
         begin
             read(x,y);
             if (x>=) then inc(sum[x-]) else
             if (x=) then inc(sum[]) else
             if (x=) then inc(sum[]) else
             if (x=) and (y=) then inc(sum[]) else
             if (x=) and (y=) then inc(sum[]);
         end;
         ans:=;
         if (sum[]>) and (sum[]>) then
         begin
             tt:=min(sum[],sum[]);
             dec(sum[],tt);
             dec(sum[],tt);
             inc(ans,tt);
         end;//double jokers
         anss:=maxlongint;
         dfs(ans+);
         writeln(anss);
         continue;
     end;
 end.