持续集成-jenkins介绍与环境搭建

什么是持续集成？

　　转自：https://blog.csdn.net/tanshizhen119/article/details/80328523

　　持续集成，俗称CI, 大师Martin Fowler对持续集成是这样定义的:持续集成是一种软件开发实践，即团队开发成员经常集成他们的工作，通常每个成员每天至少集成一次，也就意味着每天可能会发生多次集成。每次集成都通过自动化的构建（包括编译，发布，自动化测试)来验证，从而尽快地发现集成错误。许多团队发现这个过程可以大大减少集成的问题，让团队能够更快的开发内聚的软件。

按照我的理解持续集成就是，一个通过一些手段或者是工具，在整个系统开发过程中，对于某一个时段（尽可能的短）完成部分功能向整个系统集成，通过编译，单元测试，自动化脚本等方式来验证整个功能是否存在问题，从而及时的发现问题并解决问题。在持续集成过程中，还有一个最重要的概念是自动化，编译，代码扫描，测试（单元，性能等测试），包括部署到测试环境等，这些步骤尽可能的自动化。

jenkins就是一个很好的持续集成工具，它有一千多个插件，各式各样的插件多得不行，支持的语言工具也很多。而且ci在整个devops工具链中处于中心位置，负责连接各种工具。

Jenkins环境搭建

jenkins部署的方式很多，可以用tomcat, 或者运行单独的war包，按照我的习惯，我比较喜欢用docker来部署。

docker镜像地址

拉取docker镜像：docker pull jenkins

运行jenkins docker镜像：

mkdir /data/jenkins_datadocker run -d --name myjenkins -p 8080:8080 -p 50000:50000 -v /data/jenkins_data:/var/jenkins_home jenkins

就这么简单，docker就启动好了 访问：http://IP:8080

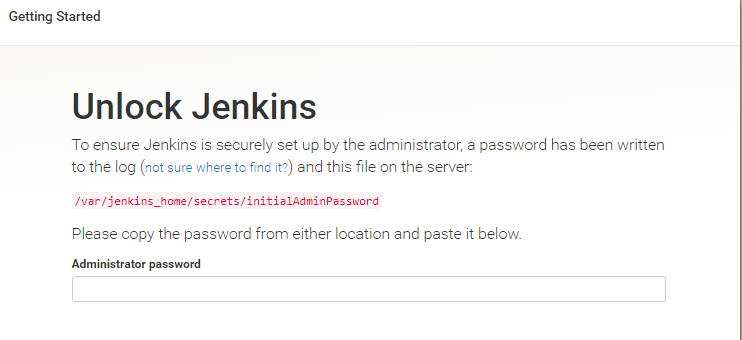
第一次登陆要输入初始密码，初始密码在 /var/jenkins_home/secrets/initialAdminPassword(这个是docker地址)

这个地址是docker里的地址，我们可以进docker里面去找：

docker exec -it myjenkins bash

cat /var/jenkins_home/secrets/initialAdminPassword

ctrl +p ,q 退出docker

另外一种方法：

由于我们启动时是否做了目录挂载：-v /data/jenkins_data:/var/jenkins_home

所以不用进docker里，直接执行 cat /data/jenkins_data/secrets/initialAdminPassword

将输入初始管理密码后，就可以进jenkins了，然后一路按照默认下载插件，然后创建一个管理员就好。

这样就已经安装好了。

jenkins功能

jenkins是一个相当出色的平台简约却不简单，整个平台提供一个最最核心的功能，但是它的插件竟然有一千多种。git, maven, ant，gerrit, gitlab, svn各种各样。只可惜免费但是不开源。

jenkins功能是相当的丰富的，但是从最最简单的来讲，它最核心的就是类似于一个作业平台。用户可以再上面创建job, 然后手动或者自动执行。它有着丰富的插件，可以让你方面的调用或者是关联各个系统或工具，来满足各式各样的要求。

我觉得jenkins2.0是引入了pipeline

什么是pipeline

什么是Pipeline，简单来说，就是一套运行于Jenkins上的工作流框架，将原本独立运行于单个或者多个节点的任务连接起来，实现单个任务难以完成的复杂发布流程。Pipeline的实现方式是一套Groovy DSL，任何发布流程都可以表述为一段Groovy脚本，并且Jenkins支持从代码库直接读取脚本，从而实现了Pipeline as Code的理念。

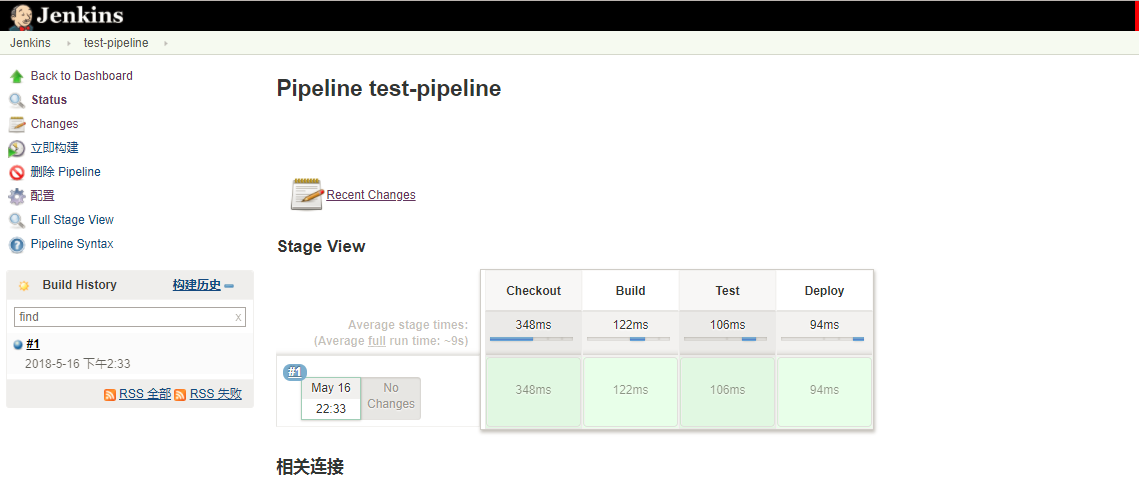
如下图就是pipeline执行的结果。这里先抛砖引玉，然后再详细介绍一下jenkins pipeline