●BZOJ 4559 [JLoi2016]成绩比较(容斥)

题链：

http://www.lydsy.com/JudgeOnline/problem.php?id=4559

题解：

容斥，拉格朗日插值法。
结合网上的另一种方法，以及插值法，可以把本题做到 O(N²)+O(N²+logN),
(本题的 O(N³)以及拉格朗日插值法在本题的用法，本篇目不再赘述。)
定义 f[k]表示至少碾压 k个人的方案数(只考虑分数相对大小关系，不考虑实际分数大小)。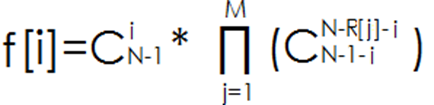

式子的含义是从N-1个人里面选K个人来碾压，然后对于每门科目，
再从没被碾压的人里选一些出来使得B神在本科目的排名为 R。
然后怎样由f[K]得到恰好有K个人被碾压的方案数ANS呢？
套路部分：
容斥系数如下：
f[K]    :1
f[K+1]    :-C(K+1,K) 
f[K+2]    :+C(K+2,K)
......
f[k+j]    :(-1)^(j)*C(k+j,k)
这些东西加起来就得到 ANS了。
容斥系数怎么推出来的呢？ 看看这个题目的解法，一样的套路，一样的味道。
求出了 ANS以后，
如果设 Y[i]表示第i门课程且B神排在第R[i]名时的分数分布方案。
则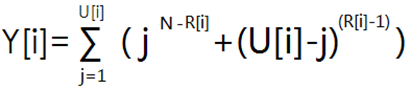
最后的答案就是 ANS*Y[1]*Y[2]*Y[3]*...*Y[M]
而这个 Y[i]可以用拉格朗日插值法求出。

代码：

#include<cstdio>
#include<cstring>
#include<iostream>
#define MAXN 105
#define _ %mod
#define filein(x) freopen(#x".in","r",stdin);
#define fileout(x) freopen(#x".out","w",stdout);
using namespace std;
const int mod=1000000007;
int dp[MAXN],U[MAXN],R[MAXN],C[MAXN][MAXN],Y[MAXN],inv[MAXN];
int N,M,K,ANS;
int pow(int a,int b){
	int now=1;
	while(b){
		if(b&1) now=(1ll*now*a)_;
		a=(1ll*a*a)_; b>>=1;
	}
	return now;
}
int Lagrange(int u,int r){
	static int lpi[MAXN],rpi[MAXN],p[MAXN],ans,tmp;
	lpi[0]=1; rpi[N+2]=1; ans=0;
	for(int i=1;i<=N+1;i++){
		p[i]=(1ll*p[i-1]+1ll*pow(i,N-r)*pow(u-i,r-1)_)_;
		if(i==u) return p[i];
	}
	for(int i=1;i<=N+1;i++) lpi[i]=1ll*lpi[i-1]*(u-i)_;
	for(int i=N+1;i>=1;i--) rpi[i]=1ll*rpi[i+1]*(u-i)_;
	for(int i=1;tmp=1,i<=N+1;i++){
		tmp=1ll*tmp*lpi[i-1]_*rpi[i+1]_*inv[i-1]_*inv[N+1-i]_*p[i]_;
		tmp=(1ll*tmp*((N+1-i)&1?-1:1)+mod)_;
		ans=(1ll*ans+tmp)_;
	}
	return ans;
}
int main()
{
	scanf("%d%d%d",&N,&M,&K);
	inv[0]=1; inv[1]=1;
	for(int i=2;i<=N+1;i++) inv[i]=((-1ll*(mod/i)*inv[mod%i])_+mod)_;
	for(int i=1;i<=N+1;i++) inv[i]=1ll*inv[i]*inv[i-1]_;
	for(int i=1;i<=M;i++) scanf("%d",&U[i]);
	for(int i=1;i<=M;i++) scanf("%d",&R[i]);
	for(int i=0;i<=N;i++){
		C[i][0]=1;
		for(int j=1;j<=i;j++)
			C[i][j]=(1ll*C[i-1][j-1]+C[i-1][j])_;
	}
	for(int i=1;i<=M;i++) Y[i]=Lagrange(U[i],R[i]);
 	for(int i=N-1;i>=K;i--)
    {
        dp[i]=C[N-1][i];
        for(int j=1;j<=M;j++)    dp[i]=1ll*dp[i]*C[N-i-1][N-R[j]-i]_;
        ANS=(1ll*ANS+(((i^K)&1)?-1:1)*1ll*dp[i]*C[i][K]_+mod)_;
    }
	for(int i=1;i<=M;i++) ANS=1ll*ANS*Y[i]_;
	printf("%d",(ANS+mod)_);
	return 0;
}