POJ 1915 Knight Moves

POJ 1915 Knight Moves

　　　　　　　　　　　　　　　　　　　　　　Knight Moves

 

Time Limit: 1000MS		Memory Limit: 30000K
Total Submissions: 29912		Accepted: 14058

Description

Background
Mr Somurolov, fabulous chess-gamer indeed, asserts that no one else
but him can move knights from one position to another so fast. Can you
beat him?

The Problem

Your task is to write a program to calculate the minimum number of
moves needed for a knight to reach one point from another, so that you
have the chance to be faster than Somurolov.

For people not familiar with chess, the possible knight moves are shown in Figure 1.

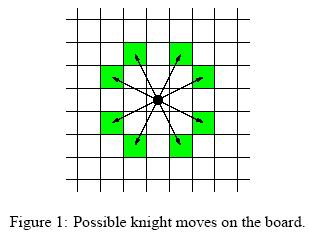
Input

The input begins with the number n of scenarios on a single line by itself.

Next follow n scenarios. Each scenario consists of three lines
containing integer numbers. The first line specifies the length l of a
side of the chess board (4 <= l <= 300). The entire board has size
l * l. The second and third line contain pair of integers {0, ...,
l-1}*{0, ..., l-1} specifying the starting and ending position of the
knight on the board. The integers are separated by a single blank. You
can assume that the positions are valid positions on the chess board of
that scenario.

Output

For
each scenario of the input you have to calculate the minimal amount of
knight moves which are necessary to move from the starting point to the
ending point. If starting point and ending point are equal,distance is
zero. The distance must be written on a single line.

Sample Input

3
8
0 0
7 0
100
0 0
30 50
10
1 1
1 1

Sample Output

5
28
0

Source

TUD Programming Contest 2001, Darmstadt, Germany

---

这题算是比较简单的BFS了，但数据较大，普通的BFS会超时，但用双向BFS就没有这个问题。

双向BFS

双向BFS的原理是起点和终点同时扩展节点，当遇到相同的节点时，记录答案退出。双向BFS减少了节点的扩展，效率比普通的BFS高出几倍，且内存开销小，是NOIP必备的技能。

code

#include <cstring>
#include <cstdio>
#include <queue>
using namespace std;

int read()
{
    int x=0,f=1;char c=getchar();
    while (c<'0' || c>'9'){if (c=='-')f=-1;c=getchar();}
    while (c>='0'&&c<='9'){x=(x<<1)+(x<<3)+c-48;c=getchar();}
    return x*f;
}

const int MAXN=310;
const int dx[]={0,1,1,-1,-1,2,2,-2,-2};
const int dy[]={0,2,-2,2,-2,1,-1,1,-1};
int n,ans;
bool flag;

struct dot
{
    int x,y,step;
    void in()
    {
        x=read();y=read();
        step=0;
    }

    bool operator == (struct dot tmp)
    {
        if (x==tmp.x && y==tmp.y)return true;
        return false;
    }
}Start,End;
int step[MAXN][MAXN];
bool vis[2][MAXN][MAXN];
queue<dot> Q[2];

bool ok(int x,int y)
{
    if (x<0 || x>=n)return false;
    if (y<0 || y>=n)return false;
    return true;
}

void get_next(int z)
{
    struct dot top,tmp;
    top=Q[z].front();Q[z].pop();
    for (int i=1;i<=8;i++)
    {
        tmp.step=top.step+1;
        tmp.x=top.x+dx[i];
        tmp.y=top.y+dy[i];
        if (!ok(tmp.x,tmp.y))continue;
        if (vis[1-z][tmp.x][tmp.y])
        {
            ans=tmp.step+step[tmp.x][tmp.y];
            flag=true;
            return ;
        }
        if (!vis[z][tmp.x][tmp.y])
        {
            vis[z][tmp.x][tmp.y]=true;
            Q[z].push(tmp);
            step[tmp.x][tmp.y]=tmp.step;
        }
    }
}

void bfs()
{
    while (!Q[0].empty())Q[0].pop();
    while (!Q[1].empty())Q[1].pop();
    Q[0].push(Start);Q[1].push(End);
    while (!Q[0].empty()||!Q[1].empty())
    {
        if (Q[0].front()==End)
        {
            ans=Q[0].front().step;
            return ;
        }
        if (!Q[0].empty()&&Q[0].size()<Q[1].size())get_next(0);
        else get_next(1);
        if (flag)return ;
    }
}

int main()
{
    int cas;cas=read();
    while (cas--)
    {
        flag=0;
        memset(step,0,sizeof(step));
        memset(vis,0,sizeof(vis));
        n=read();
        Start.in();End.in();
        vis[0][Start.x][Start.y]=1;
        vis[1][End.x][End.y]=1;
        bfs();
        printf("%d\n",ans);
    }
    return 0;
}

双向BFS的优化

双向BFS效率是惊人的如果运用的好，效率将会更高

让我们来分析一下，当出现一边节点特别多时，扩展节点多的一边会使节点数成指数倍增长，最终导致效率退化到单向BFS，所以我的程序便用了一个if语句，使两个BFS中的节点尽量平衡。

PS：其实这题并不需要这样判断，数据规模和节点的扩展都使得两边会差不多平衡。但这也不失是一种好的优化技巧。

点个赞吧