[SCOI 2010]字符串

Description

lxhgww最近接到了一个生成字符串的任务，任务需要他把n个1和m个0组成字符串，但是任务还要求在组成的字符串中，在任意的前k个字符中，1的个数不能少于0的个数。现在lxhgww想要知道满足要求的字符串共有多少个，聪明的程序员们，你们能帮助他吗？

Input

输入数据是一行，包括2个数字n和m

Output

输出数据是一行，包括1个数字，表示满足要求的字符串数目，这个数可能会很大，只需输出这个数除以20100403的余数

Sample Input

2 2

Sample Output

2

HINT

【数据范围】
对于30%的数据，保证1<=m<=n<=1000
对于100%的数据，保证1<=m<=n<=1000000

题解（转载）

->原文地址<-

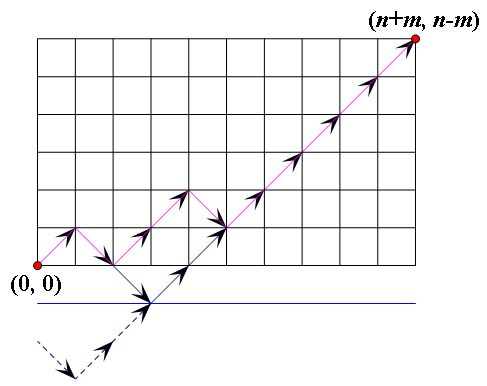
首先，我们设选$1$为$(1,1)$，选$0$为$(1,-1)$

目标就是$(n+m,n-m)$

总方案数为$C_{n+m}^n$，因为有$n+m$个位置，放$n$个$1$

然后要减去不合法的即线路通过$y=-1$的。将线路与$y=-1$交点的左边沿着$y=-1$做对称操作，则最后等价于从$(0,-2)$走到$(n+m,n-m)$的方案数

所以向上走$n-m+2$

则有$x-y=n-m+2$

　　$x+y=n+m$

　　$x=n+1,y=m-1$

所以不合法方案为$C_{n+m}^{n+1}$

$ans=C_{n+m}^n-C_{n+m}^{n+1}$

求这些用模逆元，$O(n)$求解

 //It is made by Awson on 2017.10.9
 #include <set>
 #include <map>
 #include <cmath>
 #include <ctime>
 #include <cmath>
 #include <stack>
 #include <queue>
 #include <vector>
 #include <string>
 #include <cstdio>
 #include <cstdlib>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 #define LL long long
 #define Min(a, b) ((a) < (b) ? (a) : (b))
 #define Max(a, b) ((a) > (b) ? (a) : (b))
 #define sqr(x) ((x)*(x))
 using namespace std;
 const int N = ;
 const int MOD = ;

 int n, m;
 int cnt[N+];
 int A[N+], B[N+];

 void prepare() {
   A[] = B[] = A[] = B[] =;
   for (int i = ; i <= N; i++)
     B[i] = -(LL)(MOD/i)*B[MOD%i]%MOD;
   for (int i = ; i <= N; i++)
     A[i] = (LL)A[i-]*i%MOD,
     B[i] = (LL)B[i-]*B[i]%MOD;
 }
 void work() {
   scanf("%d%d", &n, &m);
   prepare();
   printf("%lld\n", ((LL)A[m+n]*B[m]%MOD*B[n]%MOD-(LL)A[m+n]*B[m-]%MOD*B[n+]%MOD+*MOD)%MOD);
 }
 int main() {
   work();
   return ;
 }