蓝桥杯 算法训练 ALGO-116 最大的算式

算法训练 最大的算式  

时间限制：1.0s   内存限制：256.0MB

问题描述

　　题目很简单，给出N个数字，不改变它们的相对位置，在中间加入K个乘号和N-K-1个加号，（括号随便加）使最终结果尽量大。因为乘号和加号一共就是N-1个了，所以恰好每两个相邻数字之间都有一个符号。例如：
　　N=5，K=2，5个数字分别为1、2、3、4、5，可以加成：
　　1*2*(3+4+5)=24
　　1*(2+3)*(4+5)=45
　　(1*2+3)*(4+5)=45
　　……

输入格式

　　输入文件共有二行，第一行为两个有空格隔开的整数，表示N和K，其中（2<=N<=15, 0<=K<=N-1）。第二行为 N个用空格隔开的数字（每个数字在0到9之间）。

输出格式

　　输出文件仅一行包含一个整数，表示要求的最大的结果

样例输入

5 2
1 2 3 4 5

样例输出

120

样例说明

　　(1+2+3)*4*5=120

 

题目解析：

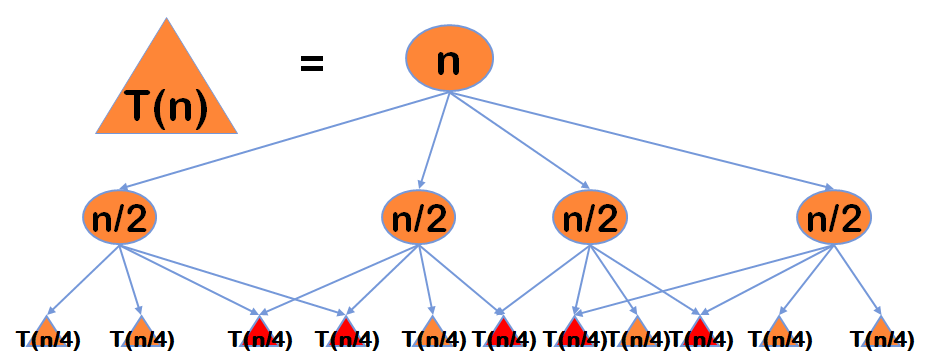
　　本题涉及到一种算法——动态规划。

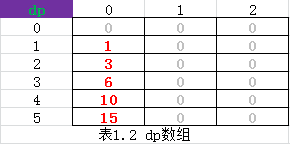
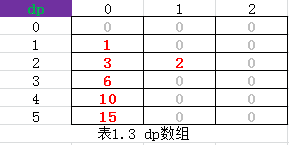
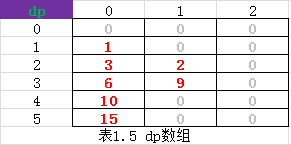
　　（1）动态规划思想

　　在分治求解过程中，有些子问题被重复计算了许多次。如果能够保存已解决的子问题的答案，而在需要时再找出，就可以避免大量重复问题的计算，从而得到多项式时间算法。

　　（2）设计动态规划的步骤　

　　　　　　① 找出最优解的性质，并刻画其结构特征；

　　　　　　② 递归地定义最优值（写出动态规划方程）；

　　　　　　③ 以自底向上的方式计算出最优值（填入表格）；

　　　　　　④ 根据计算最优值时得到的信息，构造一个最优解。

　　　　说明：　　a.步骤 ① ~ ③ 是动态规划算法的基本步骤；

　　　　　　　　　b.在只需要求出最优值的情况，步骤 ④ 可以省略；若需要求出一个最优解，则必须要有第 ④ 步。

　　（3）动态规划的特征

　　　　① 最优子结构

　　　　　　　　当问题的最优解包含了其子问题的最优解，称该问题具有最优子结构性质。

　　　　② 重叠子问题

　　　　　　　　在用递归算法自顶向下解问题时，每次产生的子问题并不总是新问题，有些子问题被反复计算多次。动态规划算法正是利用了这种子问题的重要性质，对每一个子问题只求    　　　　解一次，而后将其解保存在一个表格中，在以后尽可能多地利用这些子问题。

 

　　以题目给出的样例输入为例，分析动态规划算法：

　　（1）利用 sum 数组将前 i 个数之和保存。

　　　　

　　（2）利用 dp 数组来保存前 i 个数有 0 个乘号时的最大值（全加时的值，与 sum 数组相同），即 dp[i][0]；

　　　　

　　（3）在动态规划算法中，从第二（ i 从 2 开始）个数后开始加乘号，前 i 个数循环累加 i - 1 （j 从 1 开始，到 i -1 结束，且不能大于 k）个乘号，乘号位置循环从第一个数后的位置到第 i 个数前的位置（p 从 2 开始， 到 i 结束）；

　　　step 1：  i = 2　　　　j = 1　　　　p = 2　　　　　说明：前两个数，有一个乘号，位置在第二个数前面

　　　　　　　　dp[2][1] = 0　　　　　　　　　　　　  　 说明：前两个数一个乘号时，值为 0 （表1.2中 dp[2][1]）

　　　　　　　　dp[1][0] x ( sum[2] - sum[1] ) = 2　 说明：前一个数没有乘号乘上前两个数之和减去前一个数之和，即前一个数乘第二个数（1*2 = 2）

　　　　　　　　dp[2][1] = max( 0 , 2 )　　　　　　　　 说明：填入 dp 表中

　　　　　　　　

　　　step 2：  i = 3　　　　j = 1　　　　p = 2　　　　　说明：前三个数，有一个乘号，位置在第二个数前面

　　　　　　　　dp[3][1] = 0　　　　　　　　　　　　  　 说明：前三个数一个乘号时，值为 0 （表1.2中 dp[3][1]）

　　　　　　　　dp[1][0] x ( sum[3] - sum[1] ) = 2　 说明：前一个数没有乘号乘上前三个数之和减去前一个数之和，即前一个数乘前两个数之和（1*（2+3） = 5）

　　　　　　　　dp[3][1] = max( 0 , 5 )　　　　　　　　 说明：填入 dp 表中

　　　　　　　　　

 

　　　step 3：  i = 3　　　　j = 1　　　　p = 3　　　　　说明：前三个数，有一个乘号，位置在第三个数前面

　　　　　　　　dp[3][1] = 5　　　　　　　　　　　　  　 说明：前三个数一个乘号时，值为 0 （表1.2中 dp[3][1]）

　　　　　　　　dp[2][0] x ( sum[3] - sum[2] ) = 9　 说明：前两个数没有乘号乘上前三个数之和减去前两个数之和，即前一个数乘第三个数之和（（1+2）* 3） = 9）

　　　　　　　　dp[3][1] = max( 5 , 9 )　　　　　　　　 说明：填入 dp 表中

　　　　　　　　

　　　. . . . . .

　　　只到所有的循环执行结束，一共 19 步。dp 表最终结果为：

　　　　　　　　

　　　当 5 个数有 2 个乘号时，最大值应为 dp[5][2] = 120。在循环执行过程中，我们不用担心 dp[p-1][j-1] * (sum[i] - sum[p-1]) 究竟是那几个数得到的结果，而使用它的值就可以啦，这就是动态规划最重要的特性之一！

 

示例代码：

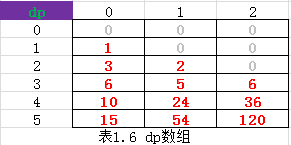
 import java.io.BufferedReader;
 import java.io.IOException;
 import java.io.InputStreamReader;

 public class Main {
     public static void main(String[] args) throws IOException {
         BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
         String[] str = br.readLine().split(" ");
         int n = Integer.parseInt(str[0]);
         int k = Integer.parseInt(str[1]);

         long[][] dp = new long[n+1][k+1];    //dp[i][j]表示前i个数中有j个乘号时，所得最大值
         int[] sum = new int[n+1];        //前i个数之和

         str = br.readLine().split(" ");
         for(int i = 1; i <= n; i++) {
             sum[i] =  sum[i-1] + Integer.parseInt(str[i-1]);
         }

         //没有乘号的情况，即连加的情况
         for(int i = 1; i <= n; i++) {
             dp[i][0] = sum[i];
         }
         //动态规划
         for(int i = 2; i <= n; i++) {                    //前i个数
             for(int j = 1; j <= i-1 && j <= k; j++) {    //乘号的个数
                 for(int p = 2; p <= i; p++) {            //乘号的位置
                     dp[i][j] = max(dp[i][j], dp[p-1][j-1] * (sum[i] - sum[p-1]));//求前i个数有j个乘号时的最大值
                 }
             }
         }

         System.out.println(dp[n][k]);
     }

     /**
      * 求最大数
      * @param a    参数1
      * @param b    参数2
      * @return    a b中的最大数
      */
     private static long max(long a, long b) {
         return a>b?a:b;
     }
 }