EM算法及其推广

概述

EM算法是一种迭代算法，用于含有隐变量(hidden variable)的概率模型参数的极大似然估计，或极大后验概率估计。

EM算法的每次迭代由两步组成：E步，求期望(expectation)；M步，求极大( maximization )，所以这一算法称为期望极大算法(expectation maximization algorithm)，简称EM算法。

 EM算法的引入

一般地，用Y表示观测随机变量的数据，Z表示隐随机变量的数据。Y和Z连在一起称为完全数据( complete-data )，观测数据Y又称为不完全数据(incomplete-data)。

假设给定观测数据Y，其概率分布是P(Y | theta)，其中theta是需要估计的模型参数，那么不完全数据Y的似然函数是P(Y | theta)，对数似然函数L(theta)=logP(Y | theta)；假设Y和Z的联合概率分布是P(Y, Z），那么完全数据的对数似然函数是log P(Y, Z | theta)。

1、EM算法定义

2、Q函数定义

完全数据的对数似然函数log P(Y, Z | theta)关于在给定观测数据Y和当前参数theta⁽ⁱ⁾下对未观测数据Z的条件概率分布P(Z | Y,theta⁽ⁱ⁾)的期望称为Q函数，即

3、EM算法说明

步骤(1)  参数的初值可以任意选择。但需注意EM算法对初值是敏感的。
步骤(2)  E步求Q(theta, theta⁽ⁱ⁾)。Q函数式中Z是未观测数据，Y是观测数据。注意，Q(theta, theta⁽ⁱ⁾)的第1个变量theta表示要极大化的参数，第2个变量theta⁽ⁱ⁾表示参数的当前估计值。每次迭代实际在求Q函数及其极大。
步骤(3)  M步求Q(theta, theta⁽ⁱ⁾)的极大化，得到theta⁽ⁱ⁺¹⁾，完成一次迭代theta⁽ⁱ⁾更新至theta⁽ⁱ⁺¹⁾。后面将证明每次迭代使似然函数增大或达到局部极值。
步骤(4)  给出停止迭代的条件，一般是对较小的正数，若满足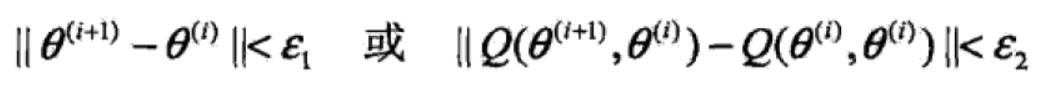则停止迭代.

4、EM算法导出

通过近似求解观测数据的对数似然函数的极大化问题来导出EM算法，由此可以清楚地看出EM算法的作用。面对一个含有隐变量的概率模型，目标是极大化观测数据(不完全数据)Y关于参数theta的对数似然函数，即极大化：

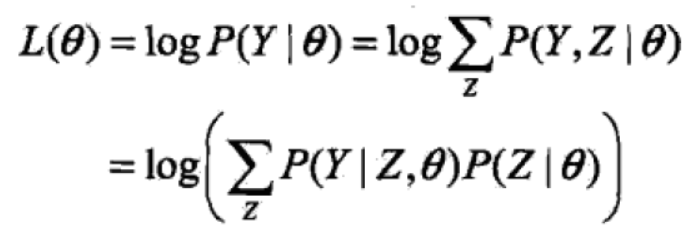
这一极大化的主要困难是式中有未观测数据并有包含和(或积分)的对数。

（1）每次迭代需要满足：新估计值 theta能使L(theta)增加，并逐步达到极大值。i次迭代前后的差值为：

（2）利用jensen不等式可以得出下界：

令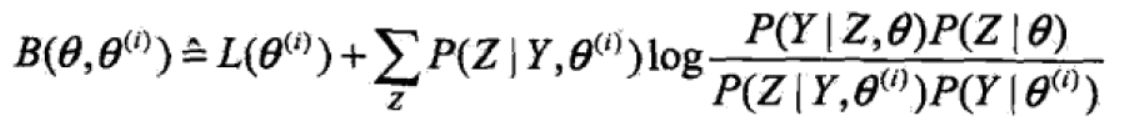

则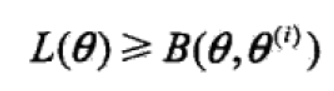且有

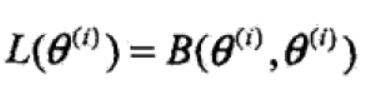
（3）选择theta⁽ⁱ⁺¹⁾使B极大：

EM算法是通过不断求解下界的极大化逼近求解对数似然函数极大化的算法，简单图示如下：

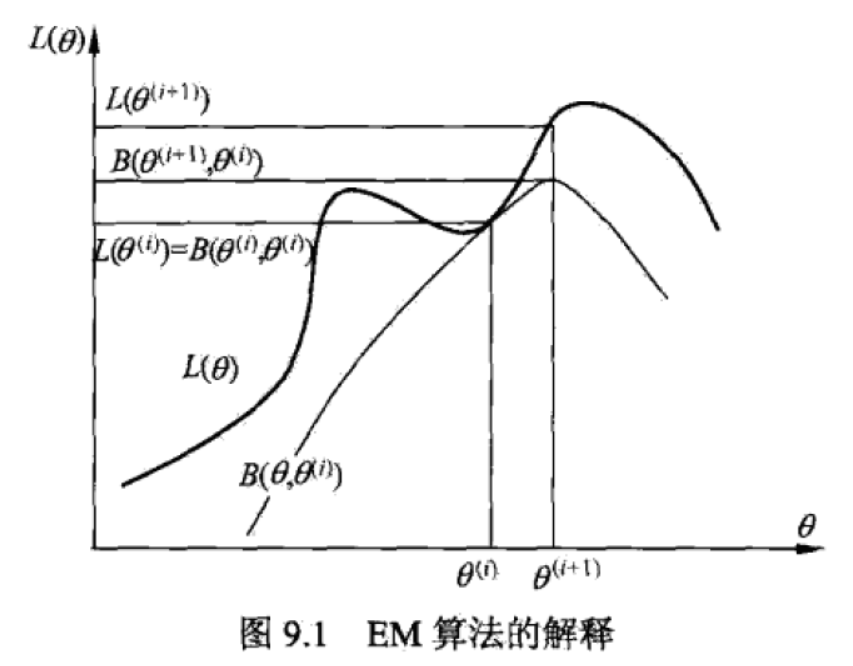
（有其他的推导方式，见博客http://www.cnblogs.com/bigmoyan/p/4550375.html还有https://www.cnblogs.com/pinard/p/6912636.html）

5、EM算法在非监督学习中的应用

训练数据只有输入没有对应的输出(X,？)，从这样的数据学习模型称为非监督学习问题。EM算法可以用于生成模型的非监督学习，生成模型由联合概率分布P(X, Y)表示，可以认为非监督学习训练数据是联合概率分布产生的数据。X为观测数据，Y为未观测数据。

EM算法的收敛性

定理9.1 设P(Y | theta)为观测数据的似然函数，theta⁽ⁱ⁾ (i=1, 2,...)为EM算法得到的参数估计序列，P(Y | theta⁽ⁱ⁾ )(i=1, 2,...))为对应的似然函数序列，则P(Y | theta⁽ⁱ⁾ )是单调递增的，即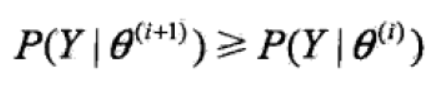

定理9.2 设P(Y | theta)为观测数据的似然函数，theta⁽ⁱ⁾ (i=1, 2,...)为EM算法得到的参数估计序列，L(theta⁽ⁱ⁾)=P(Y | theta⁽ⁱ⁾ )(i=1, 2,...))为对应的似然函数序列，
(1)如果P(Y | theta)有上界，则L(theta(i))收敛到某一值L*;
(2)在函数Q与L满足一定条件下，由EM算法得到的参数估计序列theta(i)的收敛值theta*是L(theta)的稳定点。

EM算法的收敛性包含关于对数似然函数序列L的收敛性和关于参数估计序列theta的收敛性两层意思，前者并不蕴涵后者。

此外，定理只能保证参数估计序列收敛到对数似然函数序列的稳定点，不能保证收敛到极大值点。所以在应用中，初值的选择变得非常重要，常用的办法是选取几个不同的初值进行迭代，然后对得到的各个估计值加以比较，从中选择最好的。

 

EM算法在高斯混合模型学习中的应用

1、高斯混合模型

2、推导

假设观测数据由高斯混合模型生成，，

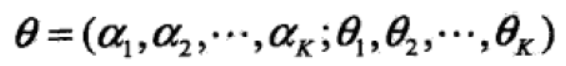
（1）明确隐变量。写出完全数据的对数似然函数

可以设想观测数据y_j是这样产生的：首先依概率a_k选择第k个高斯分布分模型；然后依第k个分模型的概率分布生成观侧数据y_j。

这时观测数据y_j是已知的；反映观测数据y_j来自第k个分模型的数据是未知的，k=1,2,... ,K，隐变量定义如下：

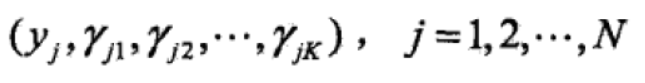
完全数据的似然函数为：

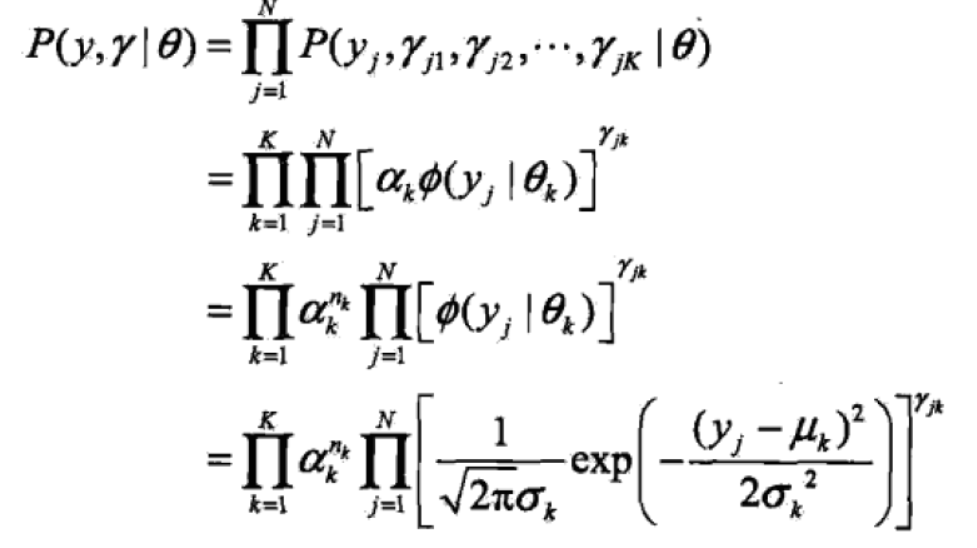其中，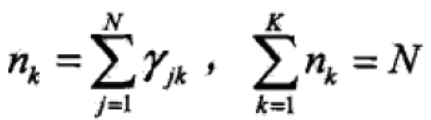

对数似然函数为：

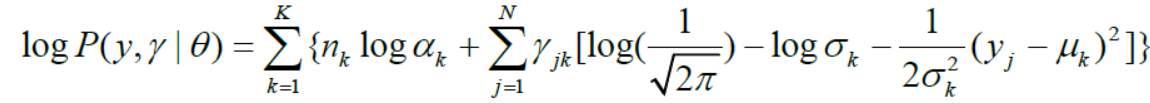
（2）EM算法的E步:确定Q函数

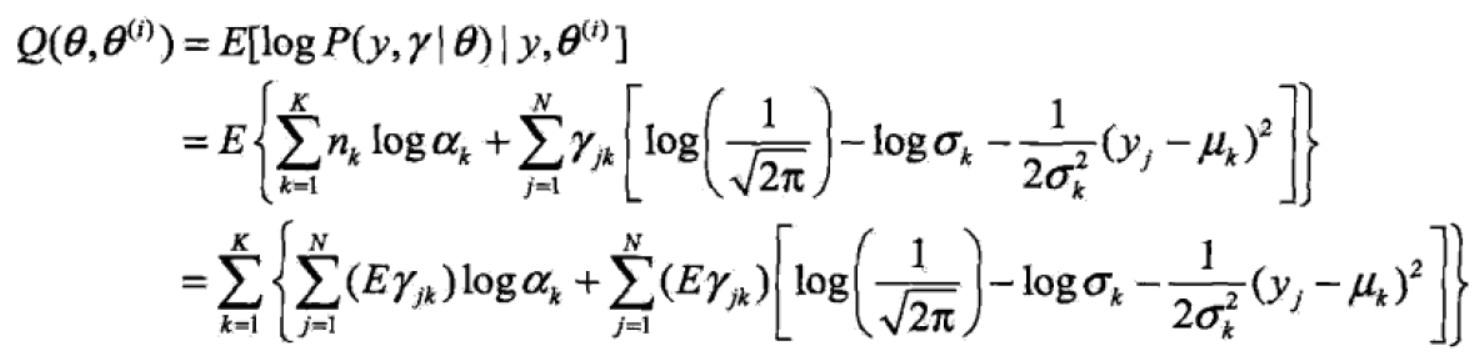
注意：第二行改错：

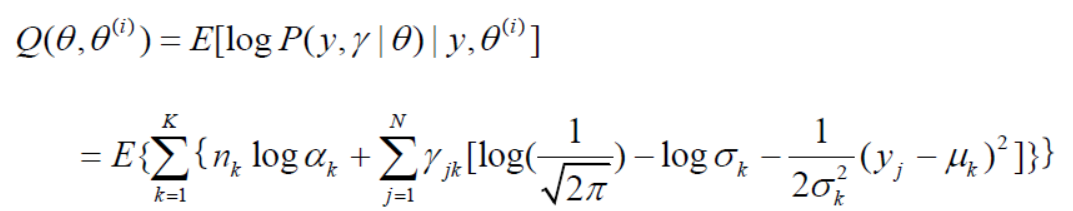
式中的那个期望计算如下：

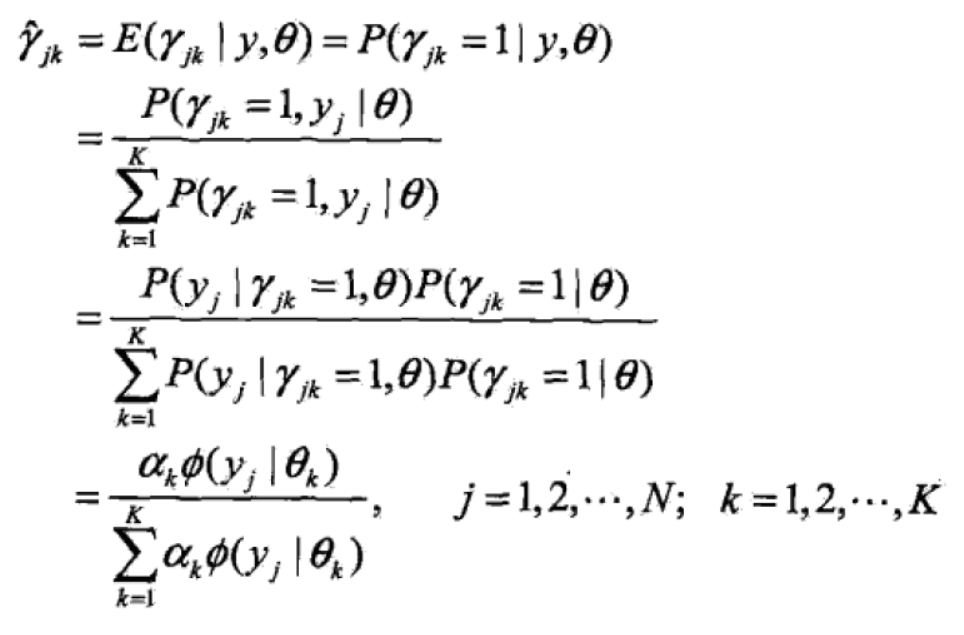
这个期望是在当前模型参数下第j个观测数据来自第k个分模型的概率，称为分模型k对观测数据y_j的响应度。

将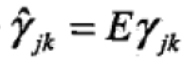和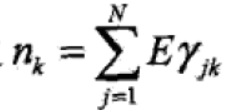代回原式得：

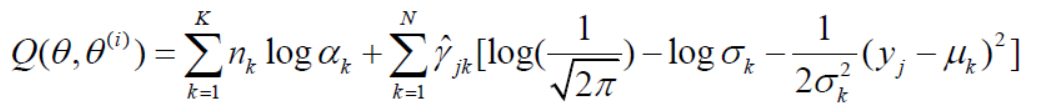
（3）确定EM算法的M步

迭代的M步是求函数Q对theta的极大值，即求新一轮迭代的模型参数：

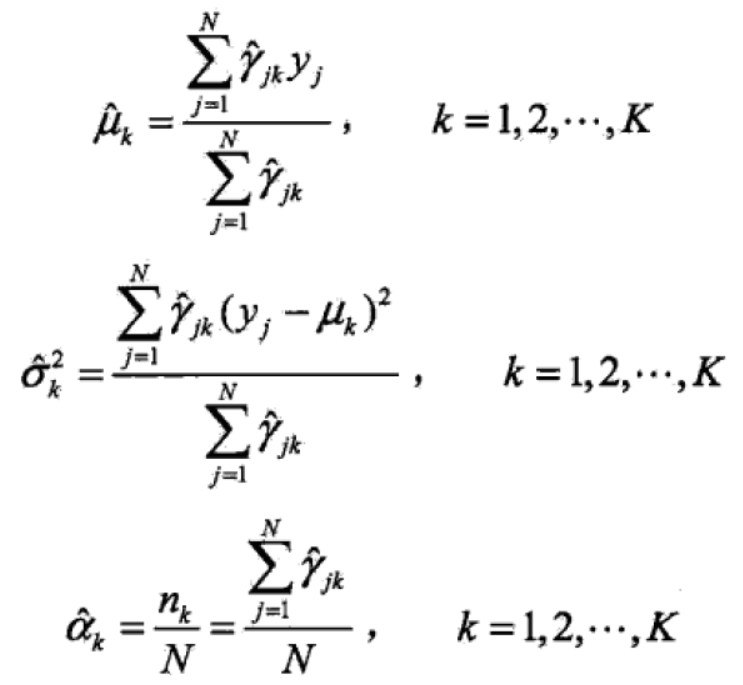
3、高斯混合模型参数估计的EM算法

EM算法的推广

EM算法还可以解释为F函数(F function)的极大-极大算法(maximization-maximization algorithm)，基于这个解释有若干变形与推广，如广义期望极大(generalized expectation maximization,  GEM)算法。

。。。不好意思，还没看懂，我后续会补。