Andrew Ng-ML-第十章-应用机器学习的建议

1.如何改进性能不好的学习算法

图1.运用到测试集上效果不佳

当进行一个正则化线性回归时，最小化了代价函数得到参数，但是运用到新的测试集上，发现效果不好，那么如何改进？

1).增加训练集。但是实际上花费的时间更多，效果并不好。

2).选取更小的特征集合。

3).获取更多特征。

4).加入多项式特征项。

5).增大/减小 正则项系数lmda。

选择这些方法时，人们大都是根据直觉来的，随便选其中一个，但是发现效果并不好。接下来会介绍一些诊断法。

2.评估假设

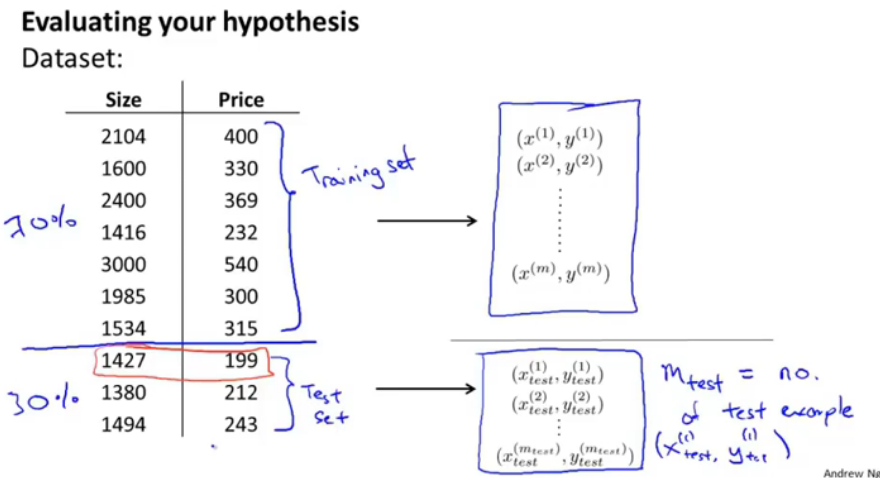
图2.选取训练集与测试集

选取总的集合的70%作为训练集，剩下30%作为test set测试集，如果整个数据集是有序的，那么应该先乱序排列再选取集合。

图3.逻辑回归中的0/1错误分类度量

最小化代价函数，注意m_test中是测试集中数据量，设置的阈值时0.5，那么当>=0.5时，y=0,以及<0.5时，y=1这两种情况都是1，else就是0，那么测试错误率就是在整个测试机上求和/m.

3.模型选择和训练、验证、测试集

图4.模型选择 

如果是进行多项式拟合的话，那么可以选择d，也就是幂次，如选择d=5时，计算其在测试集上的损失函数，很可能是最优的，那么就选d=5。

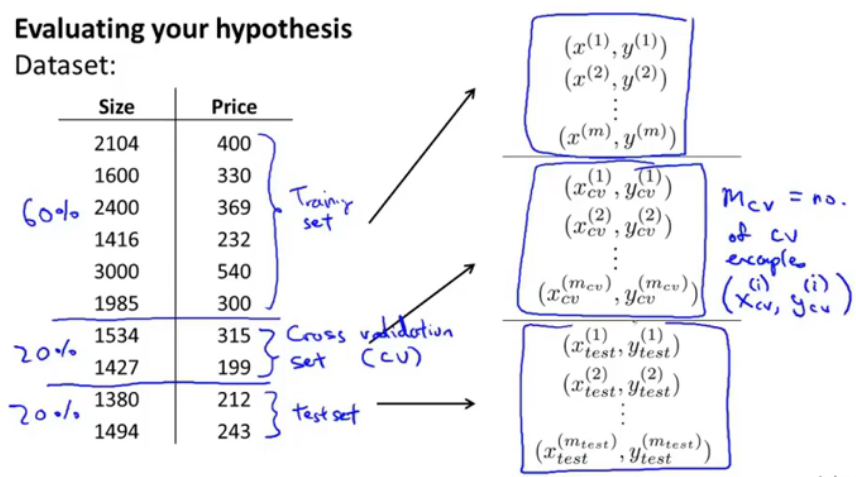
图5.训练、交叉验证、测试集

三者的比例是60%\20%\20%.通常是这样。cross validation(CV)

图6.训练、交叉验证、测试误差

图7.模型选择

首先是最小化训练误差，再计算每个模型的在验证集上的验证代价，并选择最小的，使用4模型在测试集上的估计泛化误差。当测试集较大时，将其分为验证集和测试集比较好。

4.诊断偏差与方差

如果一个学习模型表现的不好，那么有两种可能的原因，一种是偏差过大，一种是方差过大，或者两者都有关；也就是过拟合和欠拟合的问题。

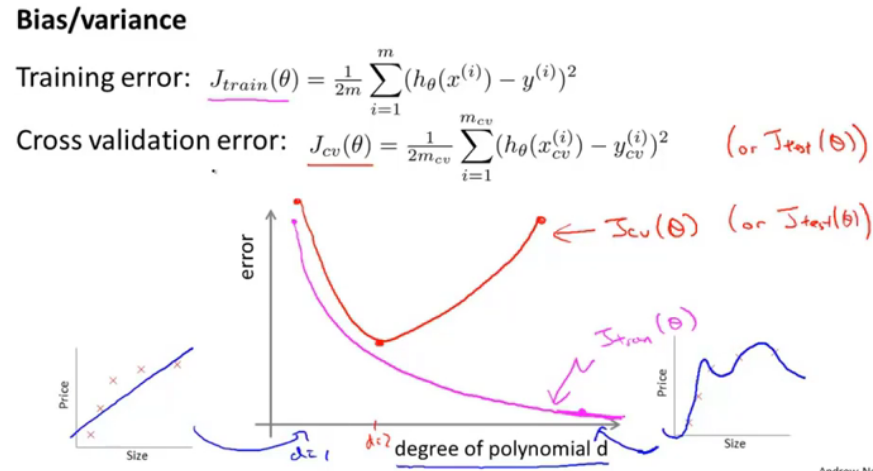
图8.偏差/方差初步

中间的图表示：横轴表示d,即最大幂次，拟合程度，紫色曲线表示训练误差，肯定是越来越小，趋近于过拟合；红色曲线表示验证误差，U型，当过小或者过大时，出现欠拟合和过拟合情况。

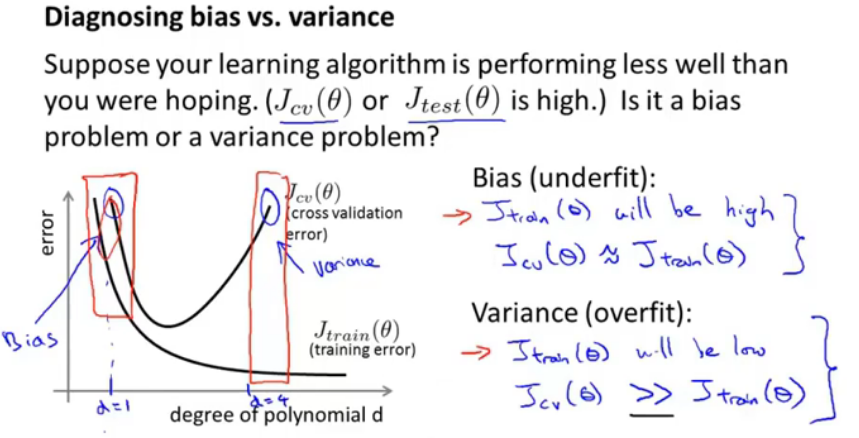
图9.方差/偏差

假如一个训练好的学习模型有着很大的验证误差代价或测试代价，那么到底是一个偏差问题还是方差问题呢？

欠拟合（偏差）：从图形上可以看出，当训练误差也很大，即训练误差≈验证误差，那么就是偏差问题。

过拟合（方差）：从图上可看出，当训练误差小时，&&验证误差远远大于训练误差，就是方差问题。

5.正则化和偏差、方差

这节深入讲解正则化是如何影响偏差和方差的。

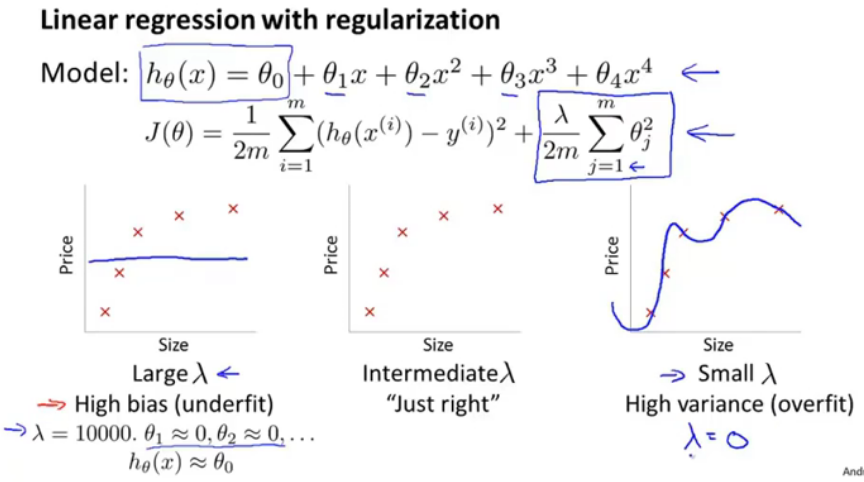
图10.线性回归中正则化与偏差、方差关系

在正则化项中，当lamd取值很大时，对参数theta的惩罚很大，那么就趋近于=theta_0，得到一条水平直线，这就是大lmda对应高偏差（欠拟合问题）。

在正则化项中，当lamd取值很小时，即相当于没有正则化，那么会出现高方差（过拟合）。

只有当lmda不大也不小时，才能够得到一个拟合度好的学习模型。

图11.如何选择一个正则化参数lmda

选择2倍长的lmda，通过最小化训练机上的代价函数得到12组不同的参数theta，并且在验证集上验证，得到一组表现最好的，就选择其theta和对应的lamd，比如说是第5组，然后在测试集上得到测试误差。

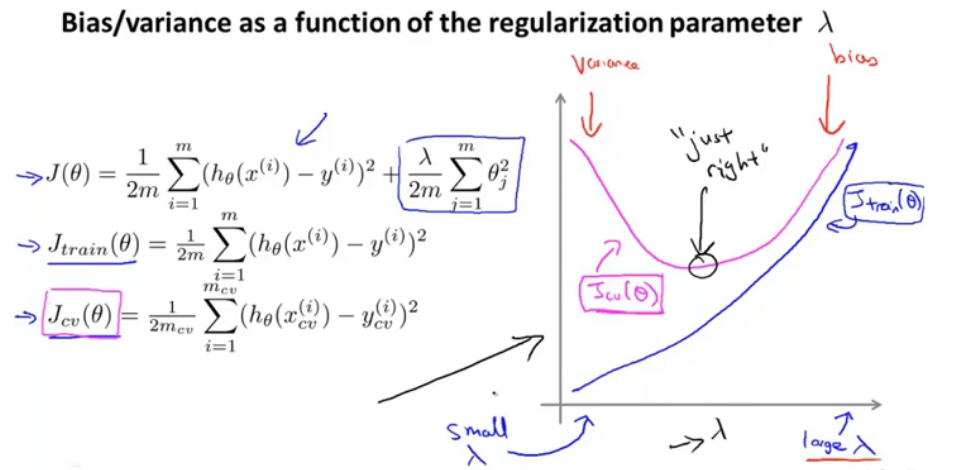
图12.lamd大小与欠拟合过拟合

训练误差曲线没有包括正则化项。

对于训练误差来说，当lamd较小时，即不进行正则化，则训练误差较小（出现高方差情况）；当lamd较大时，出现高偏差，欠拟合。

对于验证误差，是U型曲线。在实际情况下，曲线没有这么平滑，会有许多噪点。

6.学习曲线

学习曲线可以用来判断一个学习模型是偏差、方差还是二者皆有。

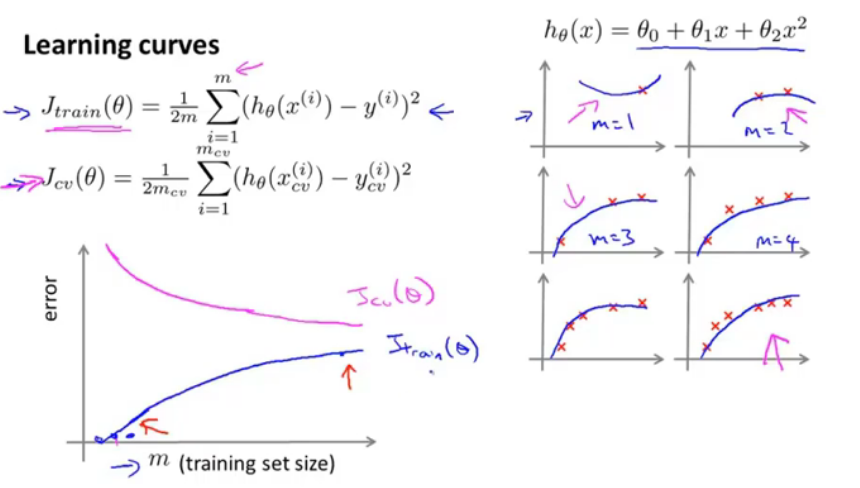
图13.学习曲线

如图的学习曲线，横轴是测试集的大小，当m=1,2,3很小时，曲线能够很好地拟合，此时训练误差=0，有正则化项时稍大于0；但是当m增大时，曲线不能够很好地拟合，训练误差会增大。

而验证误差，是相反的，这很好理解。

下面是在高偏差/高方差情况下的学习曲线。

图14.高偏差情况下的学习曲线

对于训练误差，是逐渐增大并不变保持较大，当训练集较小时还能够比较好地拟合，当训练集增大时，会逐渐增大，因为曲线基本上就固定了，所以误差持平；

对于验证误差，是逐渐减小并持平，一开始的验证误差最大，但是两者均保持较高。

对于一个学习算法如果高偏差，那么就算增加训练数据量也不能变好，更多的数据也没有意义。当你发现你的模型是高偏差的，那么应该感到幸运，因为可以确定当前学习算法无法再改进了。

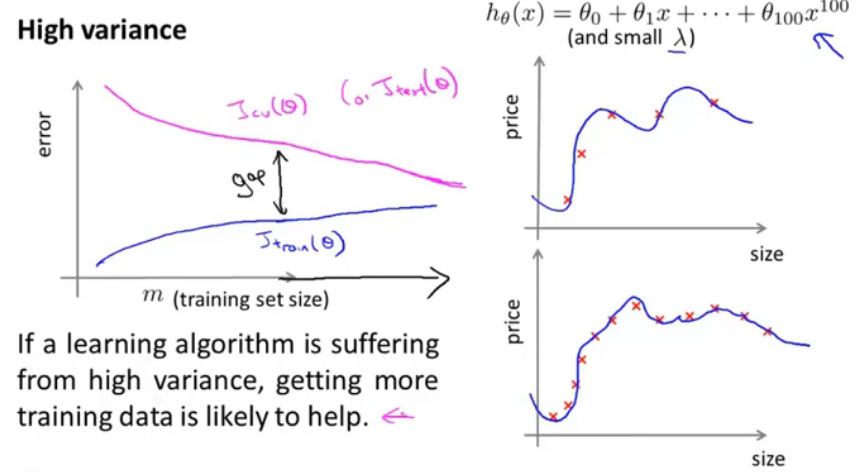
图15.高方差情况下的学习曲线

对应于过拟合的情况，当数据量较小时基本能够很密集地拟合所有的点，当数据量增大时，拟合所有数据难度增加，训练误差增大；验证误差有下降趋势；

当学习算法有高方差时，获取更多的数据可能是有帮助的。实际情况中，学习曲线可能有更多的噪声。

7.决定接下来做什么

图16.改进措施的适用情况

之前的视频中给出了学习模型表现不好的几种方法，并且给出了对应的适用情况。

1.获取更多的训练数据——高方差

2.更小的特征集——高方差

3.获取更多的特征——高偏差

4.添加多项式特征——高偏差

5.降低lmad——高偏差

6.增加lmad——高方差

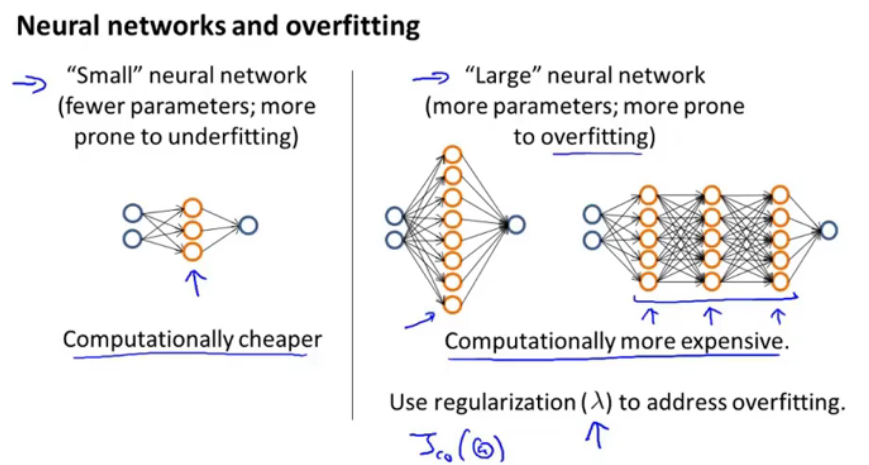
图17.如何选择神经网络

小的神经网络计算量少，参数少，可能出现欠拟合情况；大的神经网络参数更多，更可能出现过拟合情况，可以使用正则化项来很好的控制过拟合情况，计算量更大。

如何选择隐含层的层数呢？

可以像之前介绍的多个模型中如何选择d，可以将数据集分为训练、验证、测试集，分别训练出隐含层=1，2，3的情况，并且选择在验证集上表现最好的神经网络模型。